
Concept explainers
Hooke’s Law Hooke’s Law states that the force needed to keep a spring stretched x units beyond its natural length is directly proportional to x. Here the constant of proportionality is called the spring constant.
- (a) Write Hooke’s Law as an equation.
- (b) If a spring has a natural length of 5 cm and a force of 30 N is required to maintain the spring stretched to a length of 9 cm, find the spring constant.
- (c) What force is needed to keep the spring stretched to a length of 11 cm?
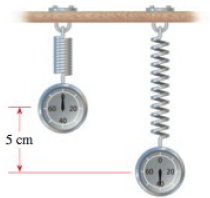
(a)
To express: Hooke’s law for spring as equation.
Answer to Problem 29E
Hooke’s law for spring is
Explanation of Solution
Hooke’s law:
The force required to keep the spring stretched beyond the natural length is directly proportional to the extension of spring beyond natural length.
Mathematically,
Here,
Thus, Hooke’s law as an equation is
(b)
To find: The spring constant
Answer to Problem 29E
The value of spring constant is
Explanation of Solution
Given:
Natural length of spring (
Force required to stretch it up to
Calculation:
The spring is stretched up to
Use Hooke’s Law,
Substitute, 30 for
Multiply both the sides by
Thus, the value of
(c)
To find: The force required to keep the spring stretched to
Answer to Problem 29E
The force required is
Explanation of Solution
Given:
The stretched length of the spring is
Calculation:
The natural length of spring is
Use Hooke’s Law,
Substitute 6 for
Thus, the value of
Chapter 1 Solutions
Precalculus - A Custom Text for UNLV
- 3) If a is a positive number, what is the value of the following double integral? 2a Love Lv 2ay-y² .x2 + y2 dadyarrow_forward16. Solve each of the following equations for x. (a) 42x+1 = 64 (b) 27-3815 (c) 92. 27² = 3-1 (d) log x + log(x - 21) = 2 (e) 3 = 14 (f) 2x+1 = 51-2xarrow_forward11. Find the composition fog and gof for the following functions. 2 (a) f(x) = 2x+5, g(x) = x² 2 (b) f(x) = x²+x, g(x) = √√x 1 (c) f(x) = -1/2) 9 9(x) = х = - Xarrow_forward
- practice problem please help!arrow_forward13. A restaurant will serve a banquet at a cost of $20 per person for the first 50 people and $15 for person for each additional person. (a) Find a function C giving the cost of the banquet depending on the number of people p attending. (b) How many people can attend the banquet for $2000?arrow_forwardAlt Fn Ctrl 12. Find functions f and g such that h(x) = (fog)(x). (a) h(x) = (x² + 2)² x+1 (b) h(x) = 5 3arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





