Chapter 1.9, Problem 13E

To determine

To graph: The quadratic equation $y=4+6x-x^2$ in a graphing window.

Explanation of Solution

Given information:

The quadratic equation $y=4+6x-x^2$ .

Graph:

The graph of the quadratic equation $y=4+6x-x^2$ can be sketched in the cartesian plane,

Consider the quadratic equation, $y=4+6x-x^2$ .

Rewrite the equation:

  $\begin{array}{l}y=4+6x-x^2\\ y=-x^2+6x+4\end{array}$

Solve the equation $y=-x^2+6x+4$ with the quadratic formula:

The quadratic formula is:

  $\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

Now solve the equation $y=-x^2+6x+4$ by quadratic formula:

Find the value of $a,b,c$ :

The value of $a,b,c$ are , $a$ is the coefficient of $x^2$ , $b$ is the coefficient of $x$ , $c$ is constant.

Thus, the value of:

  $\begin{array}{l}a=-1\\ b=6\\ c=4\end{array}$

Substitute the values of $a,b,c$ in quadratic formula:

The quadratic formula is:

  $\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

  $\begin{array}{c}\frac{-b\pm \sqrt{b^2-4ac}}{2a}=\frac{-6\pm \sqrt{6^2\times -1\times 4}}{2\times -1}\\ =\frac{\pm \sqrt{36+16}}{-2}\\ =\frac{\pm 6+4}{-2}\\ =\frac{\pm 10}{-2}\end{array}$

Either the value $\frac{\pm 10}{-2}$ is positive or negative:

When the value $\frac{\pm 10}{-2}$ is positive, then the real root is $-5$ ,

When the value $\frac{\pm 10}{-2}$ is negative, then the real root is $5$ ,

So $x=-5$ or $$

  $x=5$ ,

Here observed the equation of parabola, the coefficient of $x^2$ is negative, so the graph is opened downward.

The roots and the shape of parabola is cleared.

The graph of the equation $y=4+6x-x^2$ .

Substitute $x=0$ , in the equation $y=-x^2+6x+4$ ,

  $\begin{array}{l}y=4+6x-x^2\\ y=-x^2+6x+4\\ y=-0^2+6\cdot 0+4\\ y=4\end{array}$

Substitute $x=1$ , in the equation $y=-x^2+6x+4$ ,

  $\begin{array}{l}y=-x^2+6x+4\\ y=-{\left(1\right)}^2+6\cdot 1+4\\ y=-1+6+4\\ y=9\end{array}$

Substitute $x=2$ , in the equation $y=-x^2+6x+4$ ,

  $\begin{array}{c}y=-x^2+6x+4\\ y=-{\left(2\right)}^2+6\cdot 2+4\\ y=-4+12+4\\ y=12\end{array}$

Observe that as the value of $x$ increases there is the decrement in value of $y$ .

Steps to plot the graph of the equation $y=-x^2+6x+4$ with the help of graphing utility are as follows:

Step 1: Press $\boxed{\text{MODE}}$ key.

Step 2: Use the down arrow key to reach $\boxed{\text{FUNC}}$ option.

Step 3: Press $\boxed{\text{ENTER}}$ key.

Step 4: Press $\boxed{\text{Y=}}$ key.

Step 5: Enter the function $y=-x^2+6x+4$ .

Step 6: Press $\boxed{\text{WINDOW}}$ key. Change the settings to

  $\begin{array}{c}X\min =-10\\ X\max =10\\ Y\min =-10\\ Y\max =20\end{array}$

For better view of graph.

Step 8: Press $\boxed{\text{GRAPH}}$ key.

The result obtained on the screen is provided below,

  

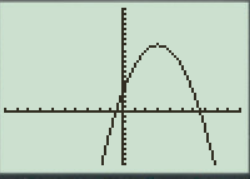
Interpretation:

The equation of the function $y=-x^2+6x+4$ represents a parabola.

The parabola opens downward.

The $x-$ intercepts are the points on $x-axis$ where the graph of the equation touches $x-axis$ .

The equation has two real roots.

The coefficients of $x^2$ is negative so the graph of the equation open downward.

Therefore value of $x$ increases then a slightly increment comes in the value of $y$ .

Therefore, the equation $y=-x^2+6x+4$ is symmetric about the $y-$ axis Initially the graph of the equation $y=-x^2+6x+4$ decreases when increase the value of $x$ ,the graph is a parabola shaped graph.