Chapter 11, Problem 17QAP

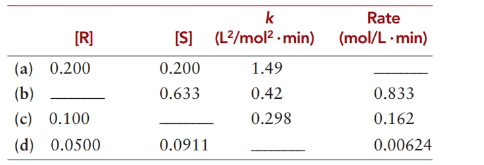
Complete the following table for the reaction

$2\text{R}\left(g\right)+3\text{S}\left(g\right)\to \text{products}$that is first-order in R and second-order in S.

Interpretation Introduction

(a)

Interpretation:

To determine the rate for the given reaction.

Concept introduction:

Rate of a chemical reaction: It tells us about the speed at which the reactants are converted into products.

Mathematically, rate of reaction is directly proportional to the product of concentration of each reactant raised to the power equal to their respective stoichiometric coefficients.

Let’s say we have a reaction:

$\begin{array}{l}\text{aA+bB}\stackrel{}{\to }\text{cC+dD}\\ \text{then,}\\ \text{rate}\text{α}{\text{[A]}}^{\text{a}}{\text{[B]}}^{\text{b}}\\ \Rightarrow \text{rate}{\text{=K}}_{\text{f}}{\text{[A]}}^{\text{a}}{\text{[B]}}^{\text{b}}\\ \text{where}{\text{K}}_{\text{f}}\text{= rate}\text{constant}\\ \text{a and b are order of reaction with respect to A and B }\\ \end{array}$

Answer to Problem 17QAP

Rate of reaction is $\text{0}\text{.01192}\text{mol/L}\text{.min}$

Explanation of Solution

Here the given chemical reaction is:

$\text{2R(g)}\text{+}\text{3S(g)}\stackrel{}{\to }\text{products}$

It is given that reaction is first order with respect to R and second order with respect with S. Thus, rate law for above reaction will be:

$\text{rate}\text{=}{\text{k[R][S]}}^{\text{2}}$

Here we have:

Concentration of R=0.200 M

Concentration of S = 0.200 M

Rate constant =1.49 L²/mol².min

Rate of reaction = let it ‘r’

Plugging value in rate law expression:

$\begin{array}{l}\text{rate}\text{=}{\text{k[R][S]}}^{\text{2}}\\ \Rightarrow \text{rate}\text{=}\text{(1}\text{.49)(0}\text{.200)(0}{\text{.200)}}^{\text{2}}\\ \Rightarrow \text{rate}\text{=}\text{0}\text{.01192}\text{mol/L}\text{.min}\end{array}$

Interpretation Introduction

(b)

Interpretation:

To determine the concentration of R in given reaction.

Concept introduction:

Rate of a chemical reaction: It tells us about the speed at which the reactants are converted into products.

Mathematically, rate of reaction is directly proportional to the product of concentration of each reactant raised to the power equal to their respective stoichiometric coefficients.

Let’s say we have a reaction:

$\begin{array}{l}\text{aA+bB}\stackrel{}{\to }\text{cC+dD}\\ \text{then,}\\ \text{rate}\text{α}{\text{[A]}}^{\text{a}}{\text{[B]}}^{\text{b}}\\ \Rightarrow \text{rate}{\text{=K}}_{\text{f}}{\text{[A]}}^{\text{a}}{\text{[B]}}^{\text{b}}\\ \text{where}{\text{K}}_{\text{f}}\text{= rate}\text{constant}\\ \text{a and b are order of reaction with respect to A and B }\\ \end{array}$

Answer to Problem 17QAP

Concentration of R is $4.95\text{mol/L}$

Explanation of Solution

Here the given chemical reaction is:

$\text{2R(g)}\text{+}\text{3S(g)}\stackrel{}{\to }\text{products}$

It is given that reaction is first order with respect to R and second order with respect with S. Thus, rate law for above reaction will be:

$\text{rate}\text{=}{\text{k[R][S]}}^{\text{2}}$

Here we have:

Concentration of R= let it ‘[R]’ mol/L

Concentration of S = 0.633 mol/L

Rate constant =0.42 L²/mol².min

Rate of reaction = 0.833 mol/L.min

Plugging value in rate law expression:

$\begin{array}{l}\text{rate}\text{=}{\text{k[R][S]}}^{\text{2}}\\ \Rightarrow 0.833\text{=}0.42\times [R]\times {\text{(0}}^{\text{.633)}}\\ \Rightarrow [R]\text{=}4.95\text{mol/L}\end{array}$

Interpretation Introduction

(c)

Interpretation:

To determine the concentration of S in given reaction.

Concept introduction:

Rate of a chemical reaction: It tells us about the speed at which the reactants are converted into products.

Mathematically, rate of reaction is directly proportional to the product of concentration of each reactant raised to the power equal to their respective stoichiometric coefficients.

Let’s say we have a reaction:

$\begin{array}{l}\text{aA+bB}\stackrel{}{\to }\text{cC+dD}\\ \text{then,}\\ \text{rate}\text{α}{\text{[A]}}^{\text{a}}{\text{[B]}}^{\text{b}}\\ \Rightarrow \text{rate}{\text{=K}}_{\text{f}}{\text{[A]}}^{\text{a}}{\text{[B]}}^{\text{b}}\\ \text{where}{\text{K}}_{\text{f}}\text{= rate}\text{constant}\\ \text{a and b are order of reaction with respect to A and B }\\ \end{array}$

Answer to Problem 17QAP

Concentration of S is $\text{2}\text{.33 mol/L}$

Explanation of Solution

Here the given chemical reaction is:

$\text{2R(g)}\text{+}\text{3S(g)}\stackrel{}{\to }\text{products}$

It is given that reaction is first order with respect to R and second order with respect with S. Thus, rate law for above reaction will be:

$\text{rate}\text{=}{\text{k[R][S]}}^{\text{2}}$

Here we have:

Concentration of R= 0.100 mol/L

Concentration of S = let it ‘[S]’ mol/L

Rate constant = 0.298 L²/mol².min

Rate of reaction = 0.162 mol/L.min

Plugging value in rate law expression:

$\begin{array}{l}\text{rate}\text{=}{\text{k[R][S]}}^{\text{2}}\\ \Rightarrow 0.162\text{=}0.298\times (0.100)\times {[}^S\\ \Rightarrow {[}^S\text{=}\frac{0.162}{0.298\times 0.100}\\ \Rightarrow {[}^S\text{=}\text{2}\text{.33 mol/L}\end{array}$

Interpretation Introduction

(d)

Interpretation:

To determine the rate constant in the given reaction.

Concept introduction:

Rate of a chemical reaction: It tells us about the speed at which the reactants are converted into products.

Mathematically, rate of reaction is directly proportional to the product of concentration of each reactant raised to the power equal to their respective stoichiometric coefficients.

Let’s say we have a reaction:

$\begin{array}{l}\text{aA+bB}\stackrel{}{\to }\text{cC+dD}\\ \text{then,}\\ \text{rate}\text{α}{\text{[A]}}^{\text{a}}{\text{[B]}}^{\text{b}}\\ \Rightarrow \text{rate}{\text{=K}}_{\text{f}}{\text{[A]}}^{\text{a}}{\text{[B]}}^{\text{b}}\\ \text{where}{\text{K}}_{\text{f}}\text{= rate}\text{constant}\\ \text{a and b are order of reaction with respect to A and B }\\ \end{array}$

Answer to Problem 17QAP

Rate constant is $\text{15}\text{.41}{\text{L}}^{\text{2}}{\text{/mol}}^2.\min$

Explanation of Solution

Here the given chemical reaction is:

$\text{2R(g)}\text{+}\text{3S(g)}\stackrel{}{\to }\text{products}$

It is given that reaction is first order with respect to R and second order with respect with S. Thus, rate law for above reaction will be:

$\text{rate}\text{=}{\text{k[R][S]}}^{\text{2}}$

Here we have:

Concentration of R= 0.0500 mol/L

Concentration of S = 0.0911 mol/L

Rate constant = let it ‘k’ L²/mol².min

Rate of reaction = 0.00624 mol/L.min

Plugging value in rate law expression:

$\begin{array}{l}\text{rate}\text{=}{\text{k[R][S]}}^{\text{2}}\\ \Rightarrow 0.0\text{0624}\text{=}\text{k×(0}\text{.0500)×(0}{\text{.0911)}}^{\text{2}}\\ \Rightarrow \text{k}\text{=}\frac{\text{0}\text{.00624}}{\text{0}\text{.0500×(0}{\text{.0911)}}^{\text{2}}}\\ \Rightarrow \text{k}\text{=}\text{15}\text{.41}{\text{L}}^{\text{2}}{\text{/mol}}^2.\min \end{array}$