
Concept explainers
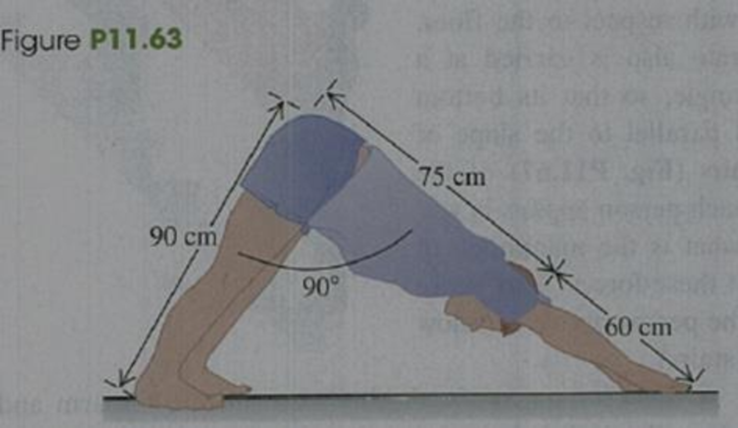
BIO Downward-Facing Dog. The yoga exercise “Downward-Facing Dog” requires stretching your hands straight out above your head and bending down to lean against the floor. This exercise is performed by a 750-N person as shown in Fig. P11.63. When he bends his body at the hip to a 90° angle between his legs and trunk, his legs, trunk, head, and arms have the dimensions indicated. Furthermore, his legs and feet weigh a total of 277 N, and their center of mass is 41 cm from his hip, measured along his legs. The person’s trunk, head, and arms weigh 473 N, and their center of gravity is 65 cm from his hip, measured along the upper body, (a) Find the normal force that the floor exerts on each foot and on each hand, assuming that the person does not favor either hand or either foot, (b) Find the friction force on each foot and on each hand, assuming that it is the same on both feet and on both hands (but not necessarily the same on the feet as on the hands). [Hint: First treat his entire body as a system; then isolate his legs (or his upper body).]
Want to see the full answer?
Check out a sample textbook solution
Chapter 11 Solutions
University Physics with Modern Physics (14th Edition)
Additional Science Textbook Solutions
Conceptual Integrated Science
College Physics: A Strategic Approach (4th Edition)
Essential University Physics (3rd Edition)
College Physics
Physics: Principles with Applications
- A 215-kg robotic arm at an assembly plant is extended horizontally (Fig. P14.32). The massless support rope attached at point B makes an angle of 15.0 with the horizontal, and the center of mass of the arm is at point C. a. What is the tension in the support rope? b. What are the magnitude and direction of the force exerted by the hinge A on the robotic arm to keep the arm in the horizontal position? FIGURE P14.32arrow_forwardRuby, with mass 55.0 kg, is trying to reach a box on a high shelf by standing on her tiptoes. In this position, half her weight is supported by the normal force exerted by the floor on the toes of each foot as shown in Figure P14.75A. This situation can be modeled mechanically by representing the force on Rubys Achilles tendon with FA and the force on her tibia as FT as shown in Figure P14.75B. What is the value of the angle and the magnitudes of the forces FA and FT? FIGURE P14.75arrow_forwardA massless, horizontal beam of length L and a massless rope support a sign of mass m (Fig. P14.78). a. What is the tension in the rope? b. In terms of m, g, d, L, and , what are the components of the force exerted by the beam on the wall? FIGURE P14.78arrow_forward
- A 5.45-N beam of uniform density is 1.60 m long. The beam is supported at an angle of 35.0 by a cable attached to one end. There is a pin through the other end of the beam (Fig. P14.30). Use the values given in the figure to find the tension in the cable. FIGURE P14.30arrow_forwardA uniform beam of length 7.60 m and weight 4.50 102 N is carried by two workers, Sam and Joe, as shown in Figure P12.6. Determine the force that each person exerts on the beam. Figure P12.6arrow_forwardA stepladder of negligible weight is constructed as shown in Figure P10.73, with AC = BC = ℓ. A painter of mass m stands on the ladder a distance d from the bottom. Assuming the floor is frictionless, find (a) the tension in the horizontal bar DE connecting the two halves of the ladder, (b) the normal forces at A and B, and (c) the components of the reaction force at the single hinge C that the left half of the ladder exerts on the right half. Suggestion: Treat the ladder as a single object, but also treat each half of the ladder separately. Figure P10.73 Problems 73 and 74.arrow_forward
- Why is the following situation impossible? A uniform beam of mass mk = 3.00 kg and length = 1.00 m supports blocks with masses m1 = 5.00 kg and m2 = 15.0 kg at two positions as shown in Figure P12.2. The beam rests on two triangular blocks, with point P a distance d = 0.300 m to the right of the center of gravity of the beam. The position of the object of mass m2 is adjusted along the length of the beam until the normal force on the beam at O is zero. Figure P12.2arrow_forwardAt a museum, a 1300-kg model aircraft is hung from a lightweight beam of length 12.0 m that is free to pivot about its base and is supported by a massless cable (Fig. P14.38). Ignore the mass of the beam. a. What is the tension in the section of the cable between the beam and the wall? b. What are the horizontal and vertical forces that the pivot exerts on the beam? FIGURE P14.38 (a) From the free-body diagram, the angle that the string tension makes with the beam is = 55.0 + 18.0 = 73.0, and the perpendicular component of the string tension is FT sin73.0. Summing torques around the base of the rod gives (Eq. 14.2): =0:(12.0m)(1300kg)(9.81m/s2)cos55.0+FT(12.0m)sin73.0=0FT=(12.0m)(1300kg)(9.81m/s2)cos55.0(12.0m)sin73.0FT=7.65103N Figure P14.38ANS (b) Using force balance (Eq. 14.1): Fx=0:FHFTcos18.0=0FH=FTcos18.0=[(12.0m)(1300kg)(9.81m/s2)cos55.0(12.0m)sin73.0]cos18.0=7.27103NFy=0:FVFTsin18.0(1300kg)(9.81m/s2)=0 FV=FTsin18.0+(1300kg)gFV=[(12.0m)(1300kg)(9.81m/s2)cos55.0(12.0m)sin73.0]sin18.0+(1300kg)(9.81m/s2)FV=1.51104Narrow_forwardA person who weighs 775 N supports himself on the ball of one foot. The normal force N = 775 N pushes up on the ball of the foot on one side of the ankle joint, while the Achilles tendon pulls up on the foot on the other side of the joint. The center of gravity of the person is located right above the tibia. What is the tension in the Achilles tendon? If the force acting is upward, enter a positive value and if the force acting is downward, enter a negative value.arrow_forward
- You can find the center of gravity of a long ruler by resting it horizontally on your two index fingers, and then slowly drawing your fingers together. First the ruler will slip on one finger, and then on the other, but eventually the fingers meet at the CG. Why does this workarrow_forwardYou can find the center of gravity of a meter stick by resting it horizontally on your two index fingers, and then slowly drawing your fingers together. First the meter stick will slip on one finger, and then on the other, but eventually the fingers meet at the CG. Why does this work?arrow_forwardA 800 N man is standing on a 4 m long plank of wood that is supported at each end by vertical ropes. The plank has a weight of 500 N and the man is standing 1 m from the left end. Find the force of tension in the rope at the left end of the plank.arrow_forward
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





