
The following rate constants were obtained in an experiment in which the decomposition of gaseous N2O; was studied as a function of temperature. The products were NO, and NO,.
| Temperature (K) | |
| 3.5 x 10_i | 298 |
| 2.2 x 10"4 | 308 |
| 6.8 X IO-4 | 318 |
| 3.1 x 10 1 | 328 |
Determine Etfor this reaction in kj/mol.
Interpretation:
Concept introduction:
Rate of a reaction can be explained using either growth of products or reduction of reactants. Both give the same rate, but our concern is different.
Every reaction has activation energy. To overcome this energy sometimes we should provide energy from outside. But for some reactions, we do not have to supply energy. Ambient temperature is enough that reactions. Those reactions are called spontaneous reactions.
Answer to Problem 11.55PAE
Solution:
Given:
- Chemical reaction
| Temperature/K | |
|
|
298 |
|
|
308 |
|
|
318 |
|
|
328 |
Explanation of Solution
The rate of the equation for the reaction can be written as follows.
- The only equation relating activation energy and rate constant is Arrhenius equation which is given below. The frequency factor doesn’t depend on the temperature.
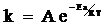
It can be written as
Therefore, at two different temperatures at
When equation 1 is subtracted from equation 2,
Formula used:
Calculation:
Want to see more full solutions like this?
Chapter 11 Solutions
Chemistry for Engineering Students
- The kinetics of a gas phase reaction of the form A → Products results in a rate constant of 0.00781 M/min. For this reaction, the initial concentration of A is 0.501 M. What is the half-life for this reaction?arrow_forwardChoose the best reagents to complete the following reaction. 1. PhNa A 2. H3O+ 1. PhCH2MgBr B 2. H3O+ хё 1. PhMgBr C 2. H3O+ 00 HO Q E D 1. H3O+ 2. PhMgBr PhMgBrarrow_forwardPlease answer all of the questions and provide detailed explanations and include a drawing to show the different signals on the molecule and include which ones should be highlighted.arrow_forward
- Draw the major product of this reaction. Ignore inorganic byproducts. Incorrect, 1 attempt remaining 1. LiAlH4 2. H3O+ Q OH ☑ Select to Drawarrow_forwardHow should I graph my data for the Absorbance of Pb and Fe for each mushroom? I want to compare the results to the known standard curve. Software: Excel Spreadsheets Link: https://mnscu-my.sharepoint.com/:x:/g/personal/vi2163ss_go_minnstate_edu/Eb2PfHdfEtBJiWh0ipHZ_kkBW4idWWwvpLPPtqoq2WkgbQ?rtime=HxrF0_tR3Ugarrow_forwardProvide the proper IUPAC name only for the following compound. Dashes, commas, and spaces must be used correctly, but do not use italics in Canvas.arrow_forward
- The kinetics of a gas phase reaction of the form A → Products results in a rate constant of 0.00781 M/min. For this reaction, the initial concentration of A is 0.501 M. How many minutes will it take for the concentration of A to reach 0.144 Marrow_forwardWhat is the rate for the second order reaction A → Products when [A] = 0.256 M? (k = 0.761 M⁻¹s⁻¹)arrow_forwardFor reaction N2(g) + O2(g) --> 2NO(g) Write the rate of the reaction in terms of change of NO.arrow_forward
 Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning World of Chemistry, 3rd editionChemistryISBN:9781133109655Author:Steven S. Zumdahl, Susan L. Zumdahl, Donald J. DeCostePublisher:Brooks / Cole / Cengage Learning
World of Chemistry, 3rd editionChemistryISBN:9781133109655Author:Steven S. Zumdahl, Susan L. Zumdahl, Donald J. DeCostePublisher:Brooks / Cole / Cengage Learning General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning





