Chapter 11, Problem 108RE

To determine

How many of each should be produced each day to maximize profit?

Answer to Problem 108RE

  $\boxed{x=12,y=12}$

Explanation of Solution

Given information:

A factory manufactures two kinds of ceramic figurines: a dancing girl and a mermaid. Each requires three processes: molding, painting, and glazing. The daily labour available for molding is no more than $90$ work-hours, labour available for painting does not exceed $120$ work-hours, and labour available for glazing is no more than $60$ work-hours. The dancing girl requires $3$ work-hours for moulding, $6$ work-hours for painting, and $2$ work-hours for glazing. The mermaid requires $3$ work-hours for moulding, $4$ work-hours for painting, and $3$ work-hours for glazing. If the profit on each figurine is $\$25$ for dancing girls and $\$30$ for mermaids, how many of each should be produced each day to maximize profit? If management decides to produce the number of each figurine that maximizes profit, determine which of these processes has work-hours assigned to it that are not used.

Calculation:

Let the number of dancing girl and mermaids produced each day be $x$ and $y$ .

The dancing girl requires $3$ work-hours for moulding, $6$ work-hours for painting, and $2$ work-hours for glazing. The mermaid requires $3$ work-hours for moulding, $4$ work-hours for painting, and $3$ work-hours for glazing. The work-hours available in total for molding are no more than $90$ , for painting no more than $120$ , and for glazing no more than $60$ . We can obtain linear inequalities using the circumstances given above.

  $\{\begin{array}{l}3x+3y\le 90\\ 6x+4y\le 120\\ 2x+3y\le 60\end{array}$

The number of dancing girl and mermaid figurines cannot be less than zero; hence we obtain two more inequalities as follows:

  $\{\begin{array}{l}x\ge 0\\ y\ge 0\end{array}$

The profit on each figurine is $\$25$ for a dancing girl and $\$30$ for mermaids. We can obtain the profit function as follows:

  $P=25x+30y$

Let’s sketch the linear inequalities obtained above in order to maximise the profit function to obtain the number of each type of figurines.

  

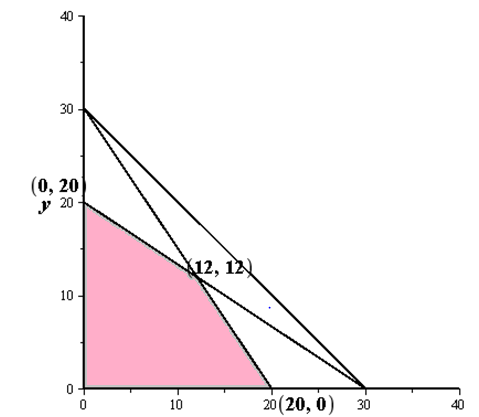
We now determine the value of the profit function at each of the corners of the feasible region obtained since the solution of the problem lies only at the corners.

  $\begin{array}{cc}\begin{array}{l}Corner\\ \left(x,y\right)\end{array}& \begin{array}{l}Value-of-the-profit-function\\ P=25x+30y\end{array}\\ (20,0)& p=25\left(20\right)+30(0)=500\\ (0,20)& P=25(0)+30(20)=600\\ (12,12)& P=25(12)+30(12)=660\end{array}$

The maximum value of the profit is attained when the number of dancing girl and mermaid to be made are $\boxed{x=12,y=12}$