
A BJT amplifier with active load is shown in Figure P10.83. The circuit contains emitter resistors

(a)
To derive:An expression for the output resistance
Answer to Problem 10.83P
Explanation of Solution
Given:
The given circuit is,
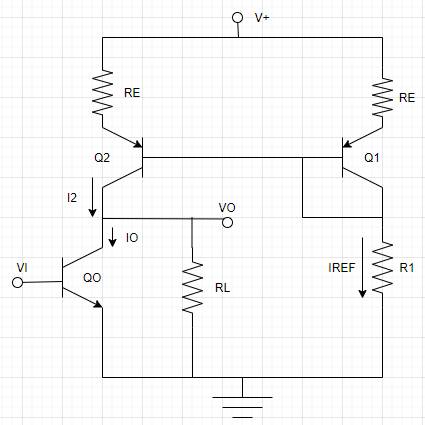
Calculation:
The small-signal equivalent circuit of BJT amplifier is as shown,
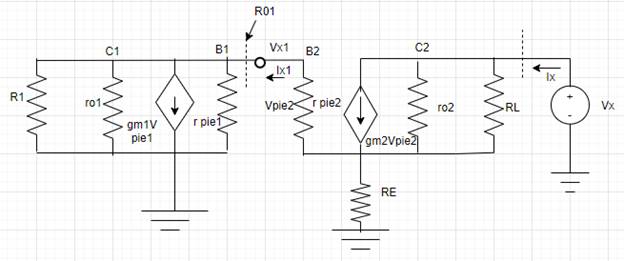
Apply KCL at base terminal of
Hybrid parameters p,
Substitute
Now rearrange the equation for output resistance
Expression for output resistance
Substitute equation (3) in equation (2)
Now the small-signal equivalent circuit is modified for output resistance as shown,
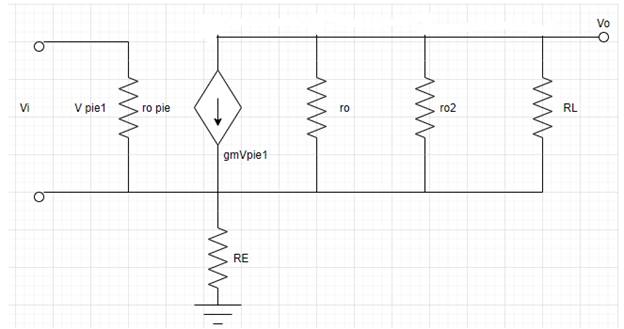
Apply KVL for input voltage at above circuit,
Expression for hybrid parameter.
Put
Rearrange the equation for output resistance,
Consider
Substitute the value of equation (10) in (9)
Conclusion:
(b)
To find:An expression for small-signal voltage gain.
Answer to Problem 10.83P
Explanation of Solution
Given:
The given circuit is,
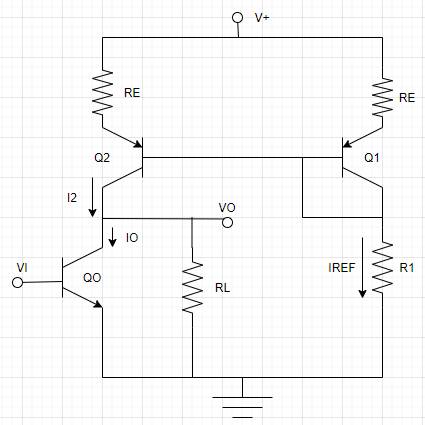
Calculation:
The small-signal equivalent circuit of BJT amplifier is as shown,
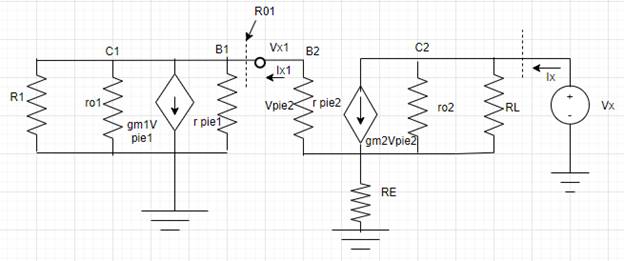
Apply KCL at base terminal of
Hybrid parameters p ,
Substitute
Now rearrange the equation for output resistance
Expression for output resistance
Substitute equation (3) in equation (2)
Now the small-signal equivalent circuit is modified for output resistance as shown, 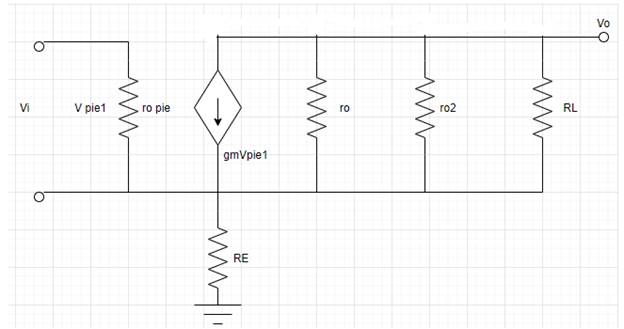
Apply KVL for input voltage at above circuit,
Expression for hybrid parameter.
Put
Rearrange the equation for output resistance,
Consider
Substitute the value of equation 10 in equation 9,
Now derive an expression for output voltage.
Input voltage will be,
Put
It is known that ,
The small-signal voltage gain derived expression is,
Conclusion:
Want to see more full solutions like this?
Chapter 10 Solutions
MICROELECT. CIRCUIT ANALYSIS&DESIGN (LL)
- A three-phase delta-connected load, each phase of which has an inductive reactance of 40 Ω and a resistance of 25 Ω, is fed from the secondary of a three-phase star-connected transformer which has a phase voltage of 230 V. Draw the circuit diagram of the system and calculate: (a) the current in each phase of the load; (b) the p.d. across each phase of the load; (c) the current in the transformer secondary windings; the total active power taken from the supply and its power factor.arrow_forwardDerive the numerical relationship between the line and phase currents for a balanced three-phase delta connected load. Three coils are connected in delta to a three-phase, three-wire, 400 V, 50 Hz supply and take a line current of 5 A 0.8 power factor lagging. Calculate the resistance and inductance of the coils. If the coils are star-connected to the same supply, calculate the line current and the total power. Calculate the line cur rents if one coil becomes open-circuited when the coils are connected in star. Ans: 110.7 Ω, 0.264 H; 1.67 A, 926 W; 1.445 A, 1.445 A, 0arrow_forwardDerive, for both star- and delta-connected systems, an expression for the total power input for a balanced three-phase load in terms of line voltage, line current and power factor. The star-connected secondary of a transformer supplies a delta-connected motor taking a power of 90 kW at a lagging power factor of 0.9. If the volt age between lines is 600 V, calculate the current in the transformer winding and in the motor winding. Draw circuit and phasor diagrams, properly labelled, showing all voltages and currents in the transformer secondary and the motor. ANS: . 96.2 A, 55.6 Aarrow_forward
- Deduce the relationship between the phase and the line voltages of a three-phase star-connected generator. If the phase voltage of a three-phase star-connected generator is 200 V, what will be the line voltages: (a) when the phases are correctly connected; (b) when the connections to one of the phases are reversed? ans: 346 V; 346 V, 200 V, 200 Varrow_forwardQ2: Given a discrete sequence x(n) = [1,-1,2,4, 1, 3,-1,1] and its spectrum X(k): i. Show that: X(k) =G(k)+WH(k) k=0,1,2,3,4,5,6,7 where G(k) = DFT[g(n)] and H(k) = DFT[h(n)], g(n) and h(n) are even and odd components of x(n) respectively. ii. Compute G(k) and H(k) using the method of computation of DFTS of two real sequences. (15 marks)arrow_forwardQ2: Given a discrete sequence x(n) = [1,-1,2,4, 1, 3,-1,1] and its spectrum X(k): i. Show that: X(k) = G(k)+WH(k) k = 0,1,2,3,4,5,6,7 where G(k) = DFT[g(n)] and H(k) = DFT[h(n)], g(n) and h(n) are even and odd components of x(n) respectively. ii. Compute G(k) and H(k) using the method of computation of DFTS of two real sequences.arrow_forward
- Q1 .For the unity feedback control system shown below, discuss the stability using Bode Plotarrow_forwardQ4: Given a discrete data array x(n₁, n2) defined as: 31 x(n₁, n₂) = 1 1 2 2 11 2. (a) Compute the two-dimensional (2-D) DFT X(k₁, k₂), using row-column (RC) algorithm. (b) Repeat part (a) using vector-radix (VR) FFT algorithm.arrow_forwardDO NOT USE AI OR CHATGPT NEED HANDWRITTEN SOLUTIONarrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





