
Concept explainers
The angle
Answer to Problem 10.61P
The angle
Explanation of Solution
Given information:
Load
A diagram with all required dimensions has been given.
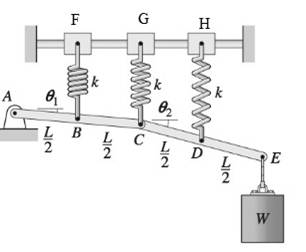
Calculation:
Consider the deflection of each spring is
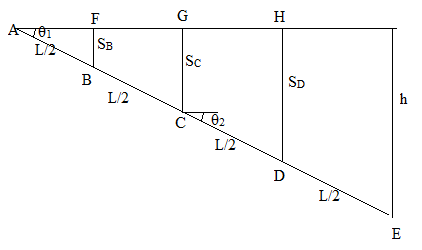
By using the geometry, deflection of each spring
The total potential energy = gravitational potential energy + potential energy of springs
Where,
Ve = Sum of potential energy of all springs
(Each value of potential energy of spring
Substituting, 2 and 3 in 1.
Now, differentiate V with respect to
Differentiating with respect to
Now, substituting
Similarly, differentiating with respect to
Now, substituting
Solving linear equations 4 and 5 simultaneously we get,
So taking inverse,
Want to see more full solutions like this?
Chapter 10 Solutions
International Edition---engineering Mechanics: Statics, 4th Edition
- Consider a 5m by 5m wet concret patio with an average water film thickness of .2mm. Now wind at 50 km/h is blowing over the surface. If the air is at 1 atm, 15oC and 35 percent relative humidity, determine how long it will take for the patio to completely dry.arrow_forward70. Compute the number of cubic centimeters of iron required for the cast-iron plate shown. The plate is 3.50 centimeters thick. Round the answer to the nearest cubic centimeter. 50.0 cm 40.0 cm Radius 150° 115.0 cm- 81.0 cmarrow_forwardLaw of Sines Solve the following problems using the Law of Sin 7. Find side x. All dimensions are in inches. -°-67°-37° 81° x Sin A 8.820 X 67°00' 32°00' a sin A b C sin B sin Carrow_forward
- 35. a. Determine B. b. Determine side b. c. Determine side c. 5.330 in.- ZB 73°30'arrow_forwardConsider a 12 cm internal diameter, 14 m long circular duct whose interior surface is wet. The duct is to be dried by forcing dry air at 1 atm and 15 degrees C throught it at an average velocity of 3m/s. The duct passes through a chilled roo, and it remains at an average temp of 15 degrees C at all time. Determine the mass transfer coeeficient in the duct.arrow_forwardnote n=number of link(dont include the ground link (fixed))arrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
