Precalculus: Graphical, Numerical, Algebraic Common Core 10th Edition
10th Edition
ISBN: 9780134673301
Author: Waits, Foley, Kennedy, Bock Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Expert Solution & Answer
Chapter P.2, Problem 20E
Solution
Find the perimeter and area of the figure determined by the points.
Perimeter = 16
Area = 16
Given information:
The given points are (-2,-2), (-2, 2) (2, 2) (2,-2)
Concept used:
- First, find the value for x on the x-axis.
- Next, find the y-value on the y-axis.
- The point should be plotted at the intersection of x and y.
- Finally, plot the point on your graph at the appropriate spot.
- Then join all the points to make a closed figure for calculating perimeter and area.
Calculation:
The given points are A(-2,-2), B(-2, 2) C(2,2) D(2,-2).
Plotting the points in the graph -
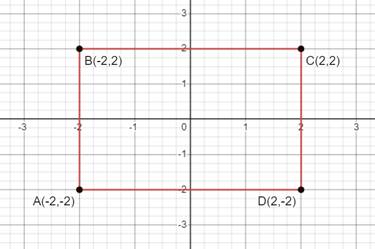
Perimeter of enclosed figure ABCD is = AB+BC+CD+DA
Using distance formula −
A(-2,-2), B(-2, 2)
AB = CD
So CD =4
B(-2, 2) C(2,2)
BC=DA
So DA=4
Perimeter of enclosed figure ABCD-
Area of enclosed figure ABCD is −
As AB=BC=CD=DA
So ABCD is a square
Area of square ABCD =
Chapter P Solutions
Precalculus: Graphical, Numerical, Algebraic Common Core 10th Edition
Ch. P.1 - Prob. 1QRCh. P.1 - Prob. 2QRCh. P.1 - Prob. 3QRCh. P.1 - Prob. 4QRCh. P.1 - Prob. 5QRCh. P.1 - Prob. 6QRCh. P.1 - Prob. 7QRCh. P.1 - Prob. 8QRCh. P.1 - Prob. 9QRCh. P.1 - Prob. 10QR
Ch. P.1 - Prob. 1ECh. P.1 - Prob. 2ECh. P.1 - Prob. 3ECh. P.1 - Prob. 4ECh. P.1 - Prob. 5ECh. P.1 - Prob. 6ECh. P.1 - Prob. 7ECh. P.1 - Prob. 8ECh. P.1 - Prob. 9ECh. P.1 - Prob. 10ECh. P.1 - Prob. 11ECh. P.1 - Prob. 12ECh. P.1 - Prob. 13ECh. P.1 - Prob. 14ECh. P.1 - Prob. 15ECh. P.1 - Prob. 16ECh. P.1 - Prob. 17ECh. P.1 - Prob. 18ECh. P.1 - Prob. 19ECh. P.1 - Prob. 20ECh. P.1 - Prob. 21ECh. P.1 - Prob. 22ECh. P.1 - Prob. 23ECh. P.1 - Prob. 24ECh. P.1 - Prob. 25ECh. P.1 - Prob. 26ECh. P.1 - Prob. 27ECh. P.1 - Prob. 28ECh. P.1 - Prob. 29ECh. P.1 - Prob. 30ECh. P.1 - Prob. 31ECh. P.1 - Prob. 32ECh. P.1 - Prob. 33ECh. P.1 - Prob. 34ECh. P.1 - Prob. 35ECh. P.1 - Prob. 36ECh. P.1 - Prob. 37ECh. P.1 - Prob. 38ECh. P.1 - Prob. 39ECh. P.1 - Prob. 40ECh. P.1 - Prob. 41ECh. P.1 - Prob. 42ECh. P.1 - Prob. 43ECh. P.1 - Prob. 44ECh. P.1 - Prob. 45ECh. P.1 - Prob. 46ECh. P.1 - Prob. 47ECh. P.1 - In Exercises 4752, simplify the expression. Assume...Ch. P.1 - In Exercises 4752, simplify the expression. Assume...Ch. P.1 - Prob. 50ECh. P.1 - Prob. 51ECh. P.1 - Prob. 52ECh. P.1 - Prob. 53ECh. P.1 - Prob. 54ECh. P.1 - Prob. 55ECh. P.1 - Prob. 56ECh. P.1 - Prob. 57ECh. P.1 - Prob. 58ECh. P.1 - Prob. 59ECh. P.1 - Prob. 60ECh. P.1 - Prob. 61ECh. P.1 - Prob. 62ECh. P.1 - Prob. 63ECh. P.1 - In Exercises 63 and 64, use scientific notation to...Ch. P.1 - Prob. 65ECh. P.1 - Prob. 66ECh. P.1 - Prob. 67ECh. P.1 - Prob. 68ECh. P.1 - Prob. 69ECh. P.1 - Prob. 70ECh. P.1 - Prob. 71ECh. P.1 - Prob. 72ECh. P.1 - Prob. 73ECh. P.1 - Prob. 74ECh. P.1 - Prob. 75ECh. P.1 - Prob. 76ECh. P.2 - Prob. 1QRCh. P.2 - Prob. 2QRCh. P.2 - Prob. 3QRCh. P.2 - Prob. 4QRCh. P.2 - Prob. 5QRCh. P.2 - Prob. 6QRCh. P.2 - Prob. 7QRCh. P.2 - Prob. 8QRCh. P.2 - Prob. 9QRCh. P.2 - Prob. 10QRCh. P.2 - Prob. 1ECh. P.2 - Prob. 2ECh. P.2 - Prob. 3ECh. P.2 - Prob. 4ECh. P.2 - Prob. 5ECh. P.2 - Prob. 6ECh. P.2 - Prob. 7ECh. P.2 - Prob. 8ECh. P.2 - Prob. 9ECh. P.2 - Prob. 10ECh. P.2 - Prob. 11ECh. P.2 - Prob. 12ECh. P.2 - Prob. 13ECh. P.2 - Prob. 14ECh. P.2 - Prob. 15ECh. P.2 - Prob. 16ECh. P.2 - Prob. 17ECh. P.2 - Prob. 18ECh. P.2 - Prob. 19ECh. P.2 - Prob. 20ECh. P.2 - Prob. 21ECh. P.2 - Prob. 22ECh. P.2 - Prob. 23ECh. P.2 - Prob. 24ECh. P.2 - Prob. 25ECh. P.2 - Prob. 26ECh. P.2 - Prob. 27ECh. P.2 - Prob. 28ECh. P.2 - Prob. 29ECh. P.2 - Prob. 30ECh. P.2 - Prob. 31ECh. P.2 - Prob. 32ECh. P.2 - Prob. 33ECh. P.2 - Prob. 34ECh. P.2 - Prob. 35ECh. P.2 - Prob. 36ECh. P.2 - Prob. 37ECh. P.2 - Prob. 38ECh. P.2 - Prob. 39ECh. P.2 - Prob. 40ECh. P.2 - Prob. 41ECh. P.2 - Prob. 42ECh. P.2 - Prob. 43ECh. P.2 - Prob. 44ECh. P.2 - Prob. 45ECh. P.2 - Prob. 46ECh. P.2 - Prob. 47ECh. P.2 - Prob. 48ECh. P.2 - Prob. 49ECh. P.2 - Prob. 50ECh. P.2 - Prob. 51ECh. P.2 - Prob. 52ECh. P.2 - Prob. 53ECh. P.2 - Prob. 54ECh. P.2 - Prob. 55ECh. P.2 - Prob. 56ECh. P.2 - Prob. 57ECh. P.2 - Prob. 58ECh. P.2 - Prob. 59ECh. P.2 - Prob. 60ECh. P.2 - Prob. 61ECh. P.2 - Prob. 62ECh. P.2 - Prob. 63ECh. P.2 - Prob. 64ECh. P.2 - Prob. 65ECh. P.2 - Prob. 66ECh. P.2 - Prob. 67ECh. P.2 - Prob. 68ECh. P.2 - Prob. 69ECh. P.2 - Prob. 70ECh. P.3 - Prob. 1QRCh. P.3 - Prob. 2QRCh. P.3 - Prob. 3QRCh. P.3 - Prob. 4QRCh. P.3 - Prob. 5QRCh. P.3 - Prob. 6QRCh. P.3 - Prob. 7QRCh. P.3 - Prob. 8QRCh. P.3 - Prob. 9QRCh. P.3 - Prob. 10QRCh. P.3 - Prob. 1ECh. P.3 - Prob. 2ECh. P.3 - Prob. 3ECh. P.3 - Prob. 4ECh. P.3 - Prob. 5ECh. P.3 - Prob. 6ECh. P.3 - Prob. 7ECh. P.3 - Prob. 8ECh. P.3 - Prob. 9ECh. P.3 - Prob. 10ECh. P.3 - Prob. 11ECh. P.3 - Prob. 12ECh. P.3 - Prob. 13ECh. P.3 - Prob. 14ECh. P.3 - Prob. 15ECh. P.3 - Prob. 16ECh. P.3 - Prob. 17ECh. P.3 - Prob. 18ECh. P.3 - Prob. 19ECh. P.3 - Prob. 20ECh. P.3 - Prob. 21ECh. P.3 - Prob. 22ECh. P.3 - Prob. 23ECh. P.3 - Prob. 24ECh. P.3 - Prob. 25ECh. P.3 - Prob. 26ECh. P.3 - Prob. 27ECh. P.3 - Prob. 28ECh. P.3 - Prob. 29ECh. P.3 - Prob. 30ECh. P.3 - Prob. 31ECh. P.3 - Prob. 32ECh. P.3 - Prob. 33ECh. P.3 - Prob. 34ECh. P.3 - Prob. 35ECh. P.3 - Prob. 36ECh. P.3 - Prob. 37ECh. P.3 - Prob. 38ECh. P.3 - Prob. 39ECh. P.3 - Prob. 40ECh. P.3 - Prob. 41ECh. P.3 - Prob. 42ECh. P.3 - Prob. 43ECh. P.3 - Prob. 44ECh. P.3 - Prob. 45ECh. P.3 - Prob. 46ECh. P.3 - Prob. 47ECh. P.3 - Prob. 48ECh. P.3 - Prob. 49ECh. P.3 - Prob. 50ECh. P.3 - Prob. 51ECh. P.3 - Prob. 52ECh. P.3 - Prob. 53ECh. P.3 - Prob. 54ECh. P.3 - Prob. 55ECh. P.3 - Prob. 56ECh. P.3 - Prob. 57ECh. P.3 - Prob. 58ECh. P.3 - Prob. 59ECh. P.3 - Prob. 60ECh. P.3 - Prob. 61ECh. P.3 - Prob. 62ECh. P.3 - Prob. 63ECh. P.3 - Prob. 64ECh. P.3 - Prob. 65ECh. P.3 - Prob. 66ECh. P.3 - Prob. 67ECh. P.3 - Prob. 68ECh. P.3 - Prob. 69ECh. P.3 - Prob. 70ECh. P.3 - Prob. 71ECh. P.3 - Prob. 72ECh. P.3 - Prob. 73ECh. P.4 - Prob. 1QRCh. P.4 - Prob. 2QRCh. P.4 - Prob. 3QRCh. P.4 - Prob. 4QRCh. P.4 - Prob. 5QRCh. P.4 - Prob. 6QRCh. P.4 - Prob. 7QRCh. P.4 - Prob. 8QRCh. P.4 - Prob. 9QRCh. P.4 - Prob. 10QRCh. P.4 - Prob. 1ECh. P.4 - Prob. 2ECh. P.4 - Prob. 3ECh. P.4 - Prob. 4ECh. P.4 - Prob. 5ECh. P.4 - Prob. 6ECh. P.4 - Prob. 7ECh. P.4 - Prob. 8ECh. P.4 - Prob. 9ECh. P.4 - Prob. 10ECh. P.4 - Prob. 11ECh. P.4 - Prob. 12ECh. P.4 - Prob. 13ECh. P.4 - Prob. 14ECh. P.4 - Prob. 15ECh. P.4 - Prob. 16ECh. P.4 - Prob. 17ECh. P.4 - Prob. 18ECh. P.4 - Prob. 19ECh. P.4 - Prob. 20ECh. P.4 - Prob. 21ECh. P.4 - Prob. 22ECh. P.4 - Prob. 23ECh. P.4 - Prob. 24ECh. P.4 - Prob. 25ECh. P.4 - Prob. 26ECh. P.4 - Prob. 27ECh. P.4 - Prob. 28ECh. P.4 - Prob. 29ECh. P.4 - Prob. 30ECh. P.4 - Prob. 31ECh. P.4 - Prob. 32ECh. P.4 - Prob. 33ECh. P.4 - Prob. 34ECh. P.4 - Prob. 35ECh. P.4 - Prob. 36ECh. P.4 - Prob. 37ECh. P.4 - Prob. 38ECh. P.4 - Prob. 39ECh. P.4 - Prob. 40ECh. P.4 - Prob. 41ECh. P.4 - Prob. 42ECh. P.4 - Prob. 43ECh. P.4 - Prob. 44ECh. P.4 - Prob. 45ECh. P.4 - Prob. 46ECh. P.4 - Prob. 47ECh. P.4 - Prob. 48ECh. P.4 - Prob. 49ECh. P.4 - Prob. 50ECh. P.4 - Prob. 51ECh. P.4 - Prob. 52ECh. P.4 - Prob. 53ECh. P.4 - Prob. 54ECh. P.4 - Prob. 55ECh. P.4 - Prob. 56ECh. P.4 - Prob. 57ECh. P.4 - Prob. 58ECh. P.4 - Prob. 59ECh. P.4 - Prob. 60ECh. P.4 - Prob. 61ECh. P.4 - Prob. 62ECh. P.4 - Prob. 63ECh. P.4 - Prob. 64ECh. P.4 - Prob. 65ECh. P.4 - Prob. 66ECh. P.4 - Prob. 67ECh. P.4 - Prob. 68ECh. P.4 - Prob. 69ECh. P.4 - Prob. 70ECh. P.4 - Prob. 71ECh. P.5 - Prob. 1QRCh. P.5 - Prob. 2QRCh. P.5 - Prob. 3QRCh. P.5 - Prob. 4QRCh. P.5 - Prob. 5QRCh. P.5 - Prob. 6QRCh. P.5 - Prob. 7QRCh. P.5 - Prob. 8QRCh. P.5 - Prob. 9QRCh. P.5 - Prob. 10QRCh. P.5 - Prob. 1ECh. P.5 - Prob. 2ECh. P.5 - Prob. 3ECh. P.5 - Prob. 4ECh. P.5 - Prob. 5ECh. P.5 - Prob. 6ECh. P.5 - Prob. 7ECh. P.5 - Prob. 8ECh. P.5 - Prob. 9ECh. P.5 - Prob. 10ECh. P.5 - Prob. 11ECh. P.5 - Prob. 12ECh. P.5 - Prob. 13ECh. P.5 - Prob. 14ECh. P.5 - Prob. 15ECh. P.5 - Prob. 16ECh. P.5 - Prob. 17ECh. P.5 - Prob. 18ECh. P.5 - Prob. 19ECh. P.5 - Prob. 20ECh. P.5 - Prob. 21ECh. P.5 - Prob. 22ECh. P.5 - Prob. 23ECh. P.5 - Prob. 24ECh. P.5 - Prob. 25ECh. P.5 - Prob. 26ECh. P.5 - Prob. 27ECh. P.5 - Prob. 28ECh. P.5 - Prob. 29ECh. P.5 - Prob. 30ECh. P.5 - Prob. 31ECh. P.5 - Prob. 32ECh. P.5 - Prob. 33ECh. P.5 - Prob. 34ECh. P.5 - Prob. 35ECh. P.5 - Prob. 36ECh. P.5 - Prob. 37ECh. P.5 - Prob. 38ECh. P.5 - Prob. 39ECh. P.5 - Prob. 40ECh. P.5 - Prob. 41ECh. P.5 - Prob. 42ECh. P.5 - Prob. 43ECh. P.5 - Prob. 44ECh. P.5 - Prob. 45ECh. P.5 - Prob. 46ECh. P.5 - Prob. 47ECh. P.5 - Prob. 48ECh. P.5 - Prob. 49ECh. P.5 - Prob. 50ECh. P.5 - Prob. 51ECh. P.5 - Prob. 52ECh. P.5 - Prob. 53ECh. P.5 - Prob. 54ECh. P.5 - Prob. 55ECh. P.5 - Prob. 56ECh. P.5 - Prob. 57ECh. P.5 - Prob. 58ECh. P.5 - Prob. 59ECh. P.5 - Prob. 60ECh. P.5 - Prob. 61ECh. P.5 - Prob. 62ECh. P.5 - Prob. 63ECh. P.5 - Prob. 64ECh. P.5 - Prob. 65ECh. P.5 - Prob. 66ECh. P.5 - Prob. 67ECh. P.5 - Prob. 68ECh. P.5 - Prob. 69ECh. P.5 - Prob. 70ECh. P.5 - Prob. 71ECh. P.6 - Prob. 1QRCh. P.6 - Prob. 2QRCh. P.6 - Prob. 3QRCh. P.6 - Prob. 4QRCh. P.6 - Prob. 5QRCh. P.6 - Prob. 6QRCh. P.6 - Prob. 7QRCh. P.6 - Prob. 8QRCh. P.6 - Prob. 9QRCh. P.6 - Prob. 10QRCh. P.6 - Prob. 1ECh. P.6 - Prob. 2ECh. P.6 - Prob. 3ECh. P.6 - Prob. 4ECh. P.6 - Prob. 5ECh. P.6 - Prob. 6ECh. P.6 - Prob. 7ECh. P.6 - Prob. 8ECh. P.6 - Prob. 9ECh. P.6 - Prob. 10ECh. P.6 - Prob. 11ECh. P.6 - Prob. 12ECh. P.6 - Prob. 13ECh. P.6 - Prob. 14ECh. P.6 - Prob. 15ECh. P.6 - Prob. 16ECh. P.6 - Prob. 17ECh. P.6 - Prob. 18ECh. P.6 - Prob. 19ECh. P.6 - Prob. 20ECh. P.6 - Prob. 21ECh. P.6 - Prob. 22ECh. P.6 - Prob. 23ECh. P.6 - Prob. 24ECh. P.6 - Prob. 25ECh. P.6 - Prob. 26ECh. P.6 - Prob. 27ECh. P.6 - Prob. 28ECh. P.6 - Prob. 29ECh. P.6 - Prob. 30ECh. P.6 - Prob. 31ECh. P.6 - Prob. 32ECh. P.6 - Prob. 33ECh. P.6 - Prob. 34ECh. P.6 - Prob. 35ECh. P.6 - Prob. 36ECh. P.6 - Prob. 37ECh. P.6 - Prob. 38ECh. P.6 - Prob. 39ECh. P.6 - Prob. 40ECh. P.6 - Prob. 41ECh. P.6 - Prob. 42ECh. P.6 - Prob. 43ECh. P.6 - Prob. 44ECh. P.6 - Prob. 45ECh. P.6 - Prob. 46ECh. P.6 - Prob. 47ECh. P.6 - Prob. 48ECh. P.6 - Prob. 49ECh. P.6 - Prob. 50ECh. P.6 - Prob. 51ECh. P.6 - Prob. 52ECh. P.6 - Prob. 53ECh. P.6 - Prob. 54ECh. P.6 - Prob. 55ECh. P.6 - Prob. 56ECh. P.6 - Prob. 57ECh. P.7 - Prob. 1QRCh. P.7 - Prob. 2QRCh. P.7 - Prob. 3QRCh. P.7 - Prob. 4QRCh. P.7 - Prob. 5QRCh. P.7 - Prob. 6QRCh. P.7 - Prob. 7QRCh. P.7 - Prob. 8QRCh. P.7 - Prob. 9QRCh. P.7 - Prob. 10QRCh. P.7 - Prob. 1ECh. P.7 - Prob. 2ECh. P.7 - Prob. 3ECh. P.7 - Prob. 4ECh. P.7 - Prob. 5ECh. P.7 - Prob. 6ECh. P.7 - Prob. 7ECh. P.7 - Prob. 8ECh. P.7 - Prob. 9ECh. P.7 - Prob. 10ECh. P.7 - Prob. 11ECh. P.7 - Prob. 12ECh. P.7 - Prob. 13ECh. P.7 - Prob. 14ECh. P.7 - Prob. 15ECh. P.7 - Prob. 16ECh. P.7 - Prob. 17ECh. P.7 - Prob. 18ECh. P.7 - Prob. 19ECh. P.7 - Prob. 20ECh. P.7 - Prob. 21ECh. P.7 - Prob. 22ECh. P.7 - Prob. 23ECh. P.7 - Prob. 24ECh. P.7 - Prob. 25ECh. P.7 - Prob. 26ECh. P.7 - Prob. 27ECh. P.7 - Prob. 28ECh. P.7 - Prob. 29ECh. P.7 - Prob. 30ECh. P.7 - Prob. 31ECh. P.7 - Prob. 32ECh. P.7 - Prob. 33ECh. P.7 - Prob. 34ECh. P.7 - Prob. 35ECh. P.7 - Prob. 36ECh. P.7 - Prob. 37ECh. P.7 - Prob. 38ECh. P.7 - Prob. 39ECh. P.7 - Prob. 40ECh. P.7 - Prob. 41ECh. P.7 - Prob. 42ECh. P.7 - Prob. 43ECh. P.7 - Prob. 44ECh. P.7 - Prob. 45ECh. P.7 - Prob. 46ECh. P.7 - Prob. 47ECh. P.7 - Prob. 48ECh. P - Prob. 1RECh. P - Prob. 2RECh. P - Prob. 3RECh. P - Prob. 4RECh. P - In Exercises 5 and 6, simplify the expression....Ch. P - Prob. 6RECh. P - Prob. 7RECh. P - Prob. 8RECh. P - Prob. 9RECh. P - Prob. 10RECh. P - Prob. 11RECh. P - Prob. 12RECh. P - Prob. 13RECh. P - Prob. 14RECh. P - Prob. 15RECh. P - Prob. 16RECh. P - Prob. 17RECh. P - Prob. 18RECh. P - Prob. 19RECh. P - Prob. 20RECh. P - Prob. 21RECh. P - Prob. 22RECh. P - Prob. 23RECh. P - Prob. 24RECh. P - Prob. 25RECh. P - Prob. 26RECh. P - Prob. 27RECh. P - Prob. 28RECh. P - Prob. 29RECh. P - Prob. 30RECh. P - Prob. 31RECh. P - Prob. 32RECh. P - Prob. 33RECh. P - Prob. 34RECh. P - Prob. 35RECh. P - Prob. 36RECh. P - Prob. 37RECh. P - Prob. 38RECh. P - Prob. 39RECh. P - Prob. 40RECh. P - Prob. 41RECh. P - Prob. 42RECh. P - Prob. 43RECh. P - Prob. 44RECh. P - Prob. 45RECh. P - Prob. 46RECh. P - Prob. 47RECh. P - Prob. 48RECh. P - Prob. 49RECh. P - Prob. 50RECh. P - Prob. 51RECh. P - Prob. 52RECh. P - Prob. 53RECh. P - Prob. 54RECh. P - Prob. 55RECh. P - Prob. 56RECh. P - Prob. 57RECh. P - Prob. 58RECh. P - Prob. 59RECh. P - Prob. 60RECh. P - Prob. 61RECh. P - Prob. 62RECh. P - Prob. 63RECh. P - Prob. 64RECh. P - Prob. 65RECh. P - Prob. 66RECh. P - Prob. 67RECh. P - Prob. 68RECh. P - Prob. 69RECh. P - Prob. 70RECh. P - Prob. 71RECh. P - Prob. 72RECh. P - Prob. 73RECh. P - Prob. 74RECh. P - Prob. 75RECh. P - Prob. 76RECh. P - Prob. 77RECh. P - Prob. 78RECh. P - Prob. 79RECh. P - Prob. 80RECh. P - Prob. 81RECh. P - Prob. 82RECh. P - Prob. 83RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Use the definite integral to find the area between the x-axis and f(x) over the indicated interval. Check first to see if the graph crosses the x-axis in the given interval. 3. f(x) = 4x; [-5,3]arrow_forwardUse the definite integral to find the area between the x-axis and f(x) over the indicated interval. Check first to see if the graph crosses the x-axis in the given interval. f(x)=3e-4; [3,3]arrow_forwardA small company of science writers found that its rate of profit (in thousands of dollars) after t years of operation is given by P'(t) = (7t + 14) (t² + 4t+7) * (a) Find the total profit in the first four years. (b) Find the profit in the sixth year of operation. (c) What is happening to the annual profit over the long run?arrow_forward
- Calculus III May I have an expert explained how the terms were simplified into 6(3-x)^2? Thank you,arrow_forwardCalculus III May I have an expert explain how the integrand was simplified into the final for form to be integrated with respect to x? Thank you,arrow_forwardCalculus lll May I please have the semicolon statement in the box defined with explanation? Thank you,arrow_forward
- 5:38 Video Message instructor Submit Question ||| Darrow_forward8:38 *** TEMU TEMU -3 -2 7 B 2 1 & 5G. 61% 1 2 -1 Based on the graph above, determine the amplitude, period, midline, and equation of the function. Use f(x) as the output. Amplitude: 2 Period: 2 Midline: 2 ☑ syntax error: this is not an equation. Function: f(x) = −2 cos(πx + 2.5π) +2× Question Help: Worked Example 1 ☑ Message instructor Submit Question ||| <arrow_forward8:39 *** TEMU 5G 60% A ferris wheel is 28 meters in diameter and boarded from a platform that is 2 meters above the ground. The six o'clock position on the ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 4 minutes. The function h = f(t) gives your height in meters above the ground t minutes after the wheel begins to turn. What is the amplitude? 14 meters What is the equation of the Midline? y = 16 What is the period? 4 meters minutes The equation that models the height of the ferris wheel after t minutes is: f(t): = ƒ (3) = ·−14(0) + 16 syntax error: you gave an equation, not an expression. syntax error. Check your variables - you might be using an incorrect one. How high are you off of the ground after 3 minutes? Round your answe the nearest meter. ||| <arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
What is a Prism? | Types of Prism | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=wxDTrgnyu28;License: Standard YouTube License, CC-BY