The mass moment of inertia of the machine component with respect to the axis through the origin characterized by the unit vector ( − 3 i − 6 j + 2 k ) / 7 .

Question

Want to see more full solutions like this?

Answer 1

Question

Chapter B, Problem B.61P

To determine

The mass moment of inertia of the machine component with respect to the axis through the origin characterized by the unit vector (−3i−6j+2k)/7.

Expert Solution & Answer

Answer to Problem B.61P

The mass moment of inertia of the machine component with respect to the axis through the origin by the unit vector is 42.75×10−3 lb⋅ft⋅s2.

Explanation of Solution

Given information:

The diameter of the formed steel wire is 18 in, unit vector is (−3i−6j+2k)/7 and the specific weight of the steel is 490 lb/ft3.

The below figure represents the schematic diagram of the wire.

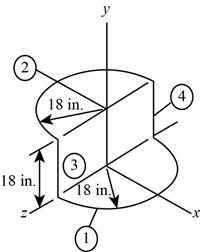
Vector Mechanics For Engineers, Chapter B, Problem B.61P

Figure-(1)

Concept used:

Expression of mass of the steel wire.

m=ρSTV ........ (I)

Here, density of the steel wire is ρST and the volume of the steel wire is V.

Expression of density of the steel wire.

ρST=γSTg ........ (II)

Here, the specific weight of the steel wire is γST and the acceleration due to gravity is g.

Substitute γSTg for ρST in Equation (I).

m=(γSTg)V ........ (III)

For section (1).

Substitute m1 for m and V1 for V in Equation (III).

m1=(γSTg)V1 ........ (IV)

Expression of volume of the steel wire after formation for section (1).

V1=(π4d12)(πd) ........ (V)

Here, the diameter of the formed wire is d1 and the diameter of the wire is d.

For section (2).

Substitute m2 for m and V2 for V in Equation (III).

m2=(γSTg)V2 ........ (VI)

Expression of volume of the steel wire after formation for section (2).

V2=(π4d12)(πd) ........ (VII)

For section (3).

Substitute m3 for m and V3 for V in Equation (III).

m3=(γSTg)V3 ........ (VIII)

Expression of volume of the steel wire after formation for section (3).

V3=(π4d12)(d) ........ (IX)

For section (4).

Substitute m4 for m and V4 for V in Equation (III).

m4=(γSTg)V4 ........ (X)

Expression of volume of the steel wire after formation for section (4).

V4=(π4d12)(d) ........ (XI)

Expression of Moment of inertia about x axis of the wire.

Ix=(Ix)1+(Ix)2+(Ix)3+(Ix)4 ........ (XII)

Here, the moment of inertia of section (1) about the x axis is (Ix)1, the moment of inertia of section (2) about the x axis is (Ix)2, the moment of inertia of section (3) about the x axis is (Ix)3 and the moment of inertia of section (4) about the x axis is (Ix)4.

Expression of moment of inertia of section (1) about the x axis.

(Ix)1=12m1d2 ........ (XIII)

Expression of moment of inertia of section (2) about the x axis.

(Ix)2=12m2d2+m2d2 ........ (XIV)

Expression of moment of inertia of section (3) about the x axis.

(Ix)3=112m3d2+m3{(d2)2+d2} ........ (XV)

Expression of moment of inertia of section (4) about the x axis.

(Ix)4=112m4d2+m4{(d2)2+d2} ........ (XVI)

Expression of Moment of inertia about y axis of the wire.

Iy=(Iy)1+(Iy)2+(Iy)3+(Iy)4 ........ (XVII)

Here, the moment of inertia of section (1) about the y axis is (Iy)1, the moment of inertia of section (2) about the y axis is (Iy)2, the moment of inertia of section (3) about the y axis is (Iy)3 and the moment of inertia of section (4) about the y axis is (Iy)4.

Expression of moment of inertia of section (1) about the y axis.

(Iy)1=m1d2 ........ (XVIII)

Expression of moment of inertia of section (2) about the y axis.

(Iy)2=m2d2 ........ (XIX)

Expression of moment of inertia of section (3) about the y axis.

(Iy)3=m3d2 ........ (XX)

Expression of moment of inertia of section (4) about the y axis.

(Iy)4=m4d2 ........ (XXI)

Expression of Moment of inertia about z axis of the wire.

Iz=(Iz)1+(Iz)2+(Iz)3+(Iz)4 ........ (XXII)

Here, the moment of inertia of section (1) about the z axis is (Iz)1, the moment of inertia of section (2) about the z axis is (Iz)2, the moment of inertia of section (3) about the z axis is (Iz)3 and the moment of inertia of section (4) about the z axis is (Iz)4.

Expression of moment of inertia of section (1) about the z axis.

(Iz)1=12m1d2 ........ (XXIII)

Expression of moment of inertia of section (2) about the z axis.

(Iz)2=12m2d2+m2d2 ........ (XXIV)

Expression of moment of inertia of section (3) about the z axis.

(Iz)3=13m3d2 ........ (XXV)

Expression of moment of inertia of section (4) about the z axis.

(Iz)4=13m4d2 ........ (XXVI)

Mass products of inertia Ixy is expressed as follows:

Ixy=∑(Ix′y′+mxy) …… (XXVII)

Here. Mass products of inertia is Ixy.

Mass products of inertia Iyz is expressed as follows:

Iyz=∑(Iyz) …… (XXVIII)

Here. Mass products of inertia is Iyz.

Mass products of inertia Izx is expressed as follows:

Izx=∑(Izx) ……(XXIX)

Here. Mass products of inertia is Izx.

Calculation:

Substitute 18 in for d1 and 18 in for d in Equation (V).

V1=(π4(18 in)2)(π(18 in))=(0.01227 in2)(π(18 in))=(0.694 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=4.016×10−4 ft3

Substitute 4.016×10−4 ft3 for V2, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (IV).

m1=(490 lb/ft332.2 ft/s2)(4.016×10−4 ft3)=(15.217 lb⋅s2/ft4)(4.016×10−4 ft3)=6.1112×10−3 lb⋅s2/ft

Substitute 18 in for d1 and 18 in for d in Equation (VII).

V2=(π4(18 in)2)(π(18 in))=(0.01227 in2)(π(18 in))=(0.694 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=4.016×10−4 ft3

Substitute 4.016×10−4 ft3 for V2, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (VI).

m2=(490 lb/ft332.2 ft/s2)(4.016×10−4 ft3)=(15.217 lb⋅s2/ft4)(4.016×10−4 ft3)=6.1112×10−3 lb⋅s2/ft

Substitute 18 in for d1 and 18 in for d in Equation (IX).

V3=(π4(18 in)2)(18 in)=(0.01227 in2)(18 in)=(0.22086 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=1.2783×10−4 ft3

Substitute 1.2783×10−4 ft3 for V3, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (VIII).

m3=(490 lb/ft332.2 ft/s2)(1.2783×10−4 ft3)=(15.217 lb⋅s2/ft4)(1.2783×10−4 ft3)=1.945×10−3 lb⋅s2/ft

Substitute 18 in for d1 and 18 in for d in Equation (XI).

V4=(π4(18 in)2)(18 in)=(0.01227 in2)(18 in)=(0.22086 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=1.2783×10−4 ft3

Substitute 1.2783×10−4 ft3 for V4, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (X).

m4=(490 lb/ft332.2 ft/s2)(1.2783×10−4 ft3)=(15.217 lb⋅s2/ft4)(1.2783×10−4 ft3)=1.945×10−3 lb⋅s2/ft

Substitute 6.1112×10−3 lb⋅s2/ft for m1 and 18 in for d in Equation (XIII).

(Ix)1=12(6.1112×10−3 lb⋅s2/ft)(18 in)2=12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=12(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=6.8751×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m2 and 18 in for d in Equation (XIV).

(Ix)2=12(6.1112×10−3 lb⋅s2/ft)(18 in)2+(6.1112×10−3 lb⋅s2/ft)(18 in)2=[12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2]=(6.8751×10−3 ft⋅s2)+(13.7502×10−3 ft⋅s2)=20.6252×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m3 and 18 in for d in Equation (XV).

(Ix)3=[112(1.945×10−3 lb⋅s2/ft)(18 in)2+(1.945×10−3 lb⋅s2/ft){(18 in2)2+(18 in)2}]=[112(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(1.945×10−3 lb⋅s2/ft)[{(18 in2)(1 ft12 in)}2+{(18 in)(1 ft12 in)}2]]=(0.3647×10−3 lb⋅ft⋅s2)+(5.4712×10−3 lb⋅ft⋅s2)=5.8359×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m4 and 18 in for d in Equation (XVI).

(Ix)4=[112(1.945×10−3 lb⋅s2/ft)(18 in)2+(1.945×10−3 lb⋅s2/ft){(18 in2)2+(18 in)2}]=[112(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(1.945×10−3 lb⋅s2/ft)[{(18 in2)(1 ft12 in)}2+{(18 in)(1 ft12 in)}2]]=(0.3647×10−3 lb⋅ft⋅s2)+(5.4712×10−3 lb⋅ft⋅s2)=5.8359×10−3 lb⋅ft⋅s2

Substitute 6.8751×10−3 lb⋅ft⋅s2 for (Ix)1, 20.6252×10−3 lb⋅ft⋅s2 for (Ix)2, 5.8359×10−3 lb⋅ft⋅s2 for (Ix)3 and 5.8359×10−3 lb⋅ft⋅s2 for (Ix)4 in Equation (XII).

Ix=[(6.8751×10−3 lb⋅ft⋅s2)+(20.6252×10−3 lb⋅ft⋅s2)+(5.8359×10−3 lb⋅ft⋅s2)+(5.8359×10−3 lb⋅ft⋅s2)]=(27.5003×10−3 lb⋅ft⋅s2)+(11.6718×10−3 lb⋅ft⋅s2)=39.1721×10−3 lb⋅ft⋅s2

Thus, the mass moment of inertia of the wire with respect to x axis is 39.1721×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m1 and 18 in for d in Equation (XVIII).

(Iy)1=(6.1112×10−3 lb⋅s2/ft)(18 in)2=(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=13.7502×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m2 and 18 in for d in Equation (XIX).

(Iy)2=(6.1112×10−3 lb⋅s2/ft)(18 in)2=(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=13.7502×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m3 and 18 in for d in Equation (XX).

(Iy)3=(1.945×10−3 lb⋅s2/ft)(18 in)2=(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=4.3769×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m4 and 18 in for d in Equation (XXI).

(Iy)4=(1.945×10−3 lb⋅s2/ft)(18 in)2=(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=4.3769×10−3 lb⋅ft⋅s2

Substitute 13.7502×10−3 lb⋅ft⋅s2 for (Iy)1, 13.7502×10−3 lb⋅ft⋅s2 for (Iy)2, 4.3769×10−3 lb⋅ft⋅s2 for (Ix)3 and 4.3769×10−3 lb⋅ft⋅s2 for (Ix)4 in Equation (XVII).

Iy=[(13.7502×10−3 lb⋅ft⋅s2)+(13.7502×10−3 lb⋅ft⋅s2)+(4.3769×10−3 lb⋅ft⋅s2)+(4.3769×10−3 lb⋅ft⋅s2)]=(27.5004×10−3 lb⋅ft⋅s2)+(8.7538×10−3 lb⋅ft⋅s2)=36.2542×10−3 lb⋅ft⋅s2

Thus, the mass moment of inertia of the wire with respect to y axis is 36.2542×10−3 lb⋅ft⋅s2.

Substitute 6.1112×10−3 lb⋅s2/ft for m1 and 18 in for d in Equation (XXIII).

(Iz)1=12(6.1112×10−3 lb⋅s2/ft)(18 in)2=12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=12(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=6.8751×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m2 and 18 in for d in Equation (XXIV).

(Iz)2=12(6.1112×10−3 lb⋅s2/ft)(18 in)2+(6.1112×10−3 lb⋅s2/ft)(18 in)2=[12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2]=(6.8751×10−3 ft⋅s2)+(13.7502×10−3 ft⋅s2)=20.6252×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m3 and 18 in for d in Equation (XXV).

(Iz)3=13(1.945×10−3 lb⋅s2/ft)(18 in)2=13(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=1.4590×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m4 and 18 in for d in Equation (XXVI).

(Iz)4=13(1.945×10−3 lb⋅s2/ft)(18 in)2=13(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=1.4590×10−3 lb⋅ft⋅s2

Substitute 6.8751×10−3 lb⋅ft⋅s2 for (Iz)1, 20.6252×10−3 lb⋅ft⋅s2 for (Iz)2, 1.4590×10−3 lb⋅ft⋅s2 for (Iz)3 and 1.4590×10−3 lb⋅ft⋅s2 for (Iz)4 in Equation (XXII).

Iz=[(6.8751×10−3 lb⋅ft⋅s2)+(20.6252×10−3 lb⋅ft⋅s2)+(1.4590×10−3 lb⋅ft⋅s2)+(1.4590×10−3 lb⋅ft⋅s2)]=(27.5003×10−3 lb⋅ft⋅s2)+(3.098×10−3 lb⋅ft⋅s2)=30.5983×10−3 lb⋅ft⋅s2

Product of inertia (Ix′y′)1,(Ix′y′)2,(Ix′y′)3,(Ix′y′)4,(Iy′z′)1,(Iy′z′)2,(Iz′x′)3,(Iz′x′)4,y1,y2,x3 and x4 are zero due to symmetry.

Substitute 0 for all product of inertia (Ix′y′) in equation (XXVII).

Ixy=∑(0+mxy)Ixy=m2x2y2Ixy=(6.1112×10−3)×(−2×18π×12)(1812)Ixy=−8.7536×10−3 lb⋅ft⋅s2

Substitute (m3y3z3)+(m4y4z4) for product of inertia ∑(Iyz) in equation (XXVIII).

Iyz=(m3y3z3)+(m4y4z4)Iyz=((1.945×10−3)×y3z3)+((1.945×10−3)y3(−z3)) (Y3=Y4z4=−z3)Iyz=0

Substitute 0 for product of inertia ∑(Izx) in equation (XXIX).

Izx=0

Mass moment of inertia of the machine component with respect to the axis through the origin by the unit vector is calculated as follows:

I=Ixλx2+Iyλy2+Izλz2−2Ixyλxλy−2Iyzλzλy−2IzxλzλxI=[(39.1721×10−3)(−37)2+(36.2542×10−3)(−67)2+(30.5983×10−3)(27)2−2×(−8.7536×10−3)(−37)(−67)−0−0]×10−3I=(7.1948+26.6357+2.4978+6.4312)×10−3I=42.75×10−3 lb⋅ft⋅s2

Conclusion:

The mass moment of inertia of the machine component with respect to the axis through the origin by the unit vector is 42.75×10−3 lb⋅ft⋅s2.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

A hot surface at 150°C is to be cooled by attaching 3-cm-long, 0.25-cm-diameter aluminum pin fins (k = 237 W/m-K) to it, with a center- to-center distance of 0.6 cm. The temperature of the surrounding medium is 30°C, and the heat transfer coefficient on the surfaces is 35 W/m²K. Determine the rate of heat transfer from the surface for a 1-m × 1-m section of the plate. Also determine the overall effectiveness of the fins. 0.6 cm 0.25 cm The total rate of heat transfer is kW. The fin effectiveness is

Consider a stainless steel spoon (k = 8.7 Btu/h·ft·°F) partially immersed in boiling water at 200°F in a kitchen at 75°F. The handle of the spoon has a cross section of 0.08 in × 0.5 in and extends 7 in in the air from the free surface of the water. The heat transfer coefficient at the exposed surfaces of the spoon handle is 3 Btu/h·ft2·°F. NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. A spoon is placed inside the container, such that the distance of the water level from the top end of the handle of the spoon is 7 meters. T sub air is indicated in the region outside the container. Identify the assumptions required to solve the problem. Check All That Apply One-dimensional heat transfer analysis is used to solve the problem. One-dimensional heat transfer analysis is used to solve the problem. Bi-dimensional heat transfer analysis is used to solve the problem. Bi-dimensional heat transfer analysis is…

A turbine blade made of a metal alloy (k=17 W/m-K) has a length of 5.3 cm, a perimeter of 11 cm, and a cross-sectional area of 5.13 cm². The turbine blade is exposed to hot gas from the combustion chamber at 1133°C with a convection heat transfer coefficient of 538 W/m²K. The base of the turbine blade maintains a constant temperature of 450°C and the tip is adiabatic. NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Hot gas h=538 W/m²K -Turbine blade k = 17 W/m-K p=11 cm, L=5.3 cm A = 5.13 cm² -T=450°C Determine the heat transfer rate to the turbine blade. W. The heat transfer rate is

Answer 2