The mass moment of inertia of the wire with respect to x ,y and z axis.

Question

Want to see more full solutions like this?

Answer 1

Question

Chapter B, Problem B.37P

To determine

The mass moment of inertia of the wire with respect to x ,y and z axis.

Expert Solution & Answer

Answer to Problem B.37P

The mass moment of inertia of the wire with respect to x axis is 39.1721×10−3 lb⋅ft⋅s2.

The mass moment of inertia of the wire with respect to y axis is 36.2542×10−3 lb⋅ft⋅s2.

The mass moment of inertia of the wire with respect to z axis is 30.5983×10−3 lb⋅ft⋅s2

Explanation of Solution

Given information:

The diameter of the formed steel wire is 18 in and the specific weight of the steel is 490 lb/ft3.

The below figure represent the schematic diagram of the wire.

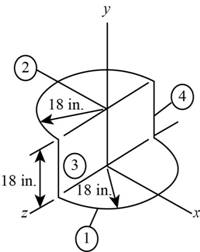
Vector Mechanics For Engineers, Chapter B, Problem B.37P

Figure-(1)

Expression of mass of the steel wire.

m=ρSTV ......(I)

Here, density of the steel wire is ρST and the volume of the steel wire is V.

Expression of density of the steel wire.

ρST=γSTg ......(II)

Here, the specific weight of the steel wire is γST and the acceleration due to gravity is g.

Substitute γSTg for ρST in Equation (I).

m=(γSTg)V ......(III)

For section (1).

Substitute m1 for m and V1 for V in Equation (III).

m1=(γSTg)V1 ......(IV)

Expression of volume of the steel wire after formation for section (1).

V1=(π4d12)(πd) ......(V)

Here, the diameter of the formed wire is d1 and the diameter of the wire is d.

For section (2).

Substitute m2 for m and V2 for V in Equation (III).

m2=(γSTg)V2 ......(VI)

Expression of volume of the steel wire after formation for section (2).

V2=(π4d12)(πd) ......(VII)

For section (3).

Substitute m3 for m and V3 for V in Equation (III).

m3=(γSTg)V3 ......(VIII)

Expression of volume of the steel wire after formation for section (3).

V3=(π4d12)(d) ......(IX)

For section (4).

Substitute m4 for m and V4 for V in Equation (III).

m4=(γSTg)V4 ......(X)

Expression of volume of the steel wire after formation for section (4).

V4=(π4d12)(d) ......(XI)

Expression of Moment of inertia about x axis of the wire.

Ix=(Ix)1+(Ix)2+(Ix)3+(Ix)4 ......(XII)

Here, the moment of inertia of section (1) about the x axis is (Ix)1, the moment of inertia of section (2) about the x axis is (Ix)2 ,the moment of inertia of section (3) about the x axis is (Ix)3 and the moment of inertia of section (4) about the x axis is (Ix)4.

Expression of moment of inertia of section (1) about the x axis.

(Ix)1=12m1d2 ......(XIII)

Expression of moment of inertia of section (2) about the x axis.

(Ix)2=12m2d2+m2d2 ......(XIV)

Expression of moment of inertia of section (3) about the x axis.

(Ix)3=112m3d2+m3{(d2)2+d2} ......(XV)

Expression of moment of inertia of section (4) about the x axis.

(Ix)4=112m4d2+m4{(d2)2+d2} ......(XVI)

Expression of Moment of inertia about y axis of the wire.

Iy=(Iy)1+(Iy)2+(Iy)3+(Iy)4 ......(XVII)

Here, the moment of inertia of section (1) about the y axis is (Iy)1, the moment of inertia of section (2) about the y axis is (Iy)2 ,the moment of inertia of section (3) about the y axis is (Iy)3 and the moment of inertia of section (4) about the y axis is (Iy)4.

Expression of moment of inertia of section (1) about the y axis.

(Iy)1=m1d2 ......(XVIII)

Expression of moment of inertia of section (2) about the y axis.

(Iy)2=m2d2 ......(XIX)

Expression of moment of inertia of section (3) about the y axis.

(Iy)3=m3d2 ......(XX)

Expression of moment of inertia of section (4) about the y axis.

(Iy)4=m4d2 ......(XXI)

Expression of Moment of inertia about z axis of the wire.

Iz=(Iz)1+(Iz)2+(Iz)3+(Iz)4 ......(XXII)

Here, the moment of inertia of section (1) about the z axis is (Iz)1, the moment of inertia of section (2) about the z axis is (Iz)2 ,the moment of inertia of section (3) about the z axis is (Iz)3 and the moment of inertia of section (4) about the z axis is (Iz)4.

Expression of moment of inertia of section (1) about the z axis.

(Iz)1=12m1d2 ......(XXIII)

Expression of moment of inertia of section (2) about the z axis.

(Iz)2=12m2d2+m2d2 ......(XXIV)

Expression of moment of inertia of section (3) about the z axis.

(Iz)3=13m3d2 ......(XXV)

Expression of moment of inertia of section (4) about the z axis.

(Iz)4=13m4d2 ......(XXVI)

Calculation:

Substitute 18 in for d1 and 18 in for d in Equation (V).

V1=(π4(18 in)2)(π(18 in))=(0.01227 in2)(π(18 in))=(0.694 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=4.016×10−4 ft3

Substitute 4.016×10−4 ft3 for V2, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (IV).

m1=(490 lb/ft332.2 ft/s2)(4.016×10−4 ft3)=(15.217 lb⋅s2/ft4)(4.016×10−4 ft3)=6.1112×10−3 lb⋅s2/ft

Substitute 18 in for d1 and 18 in for d in Equation (VII).

V2=(π4(18 in)2)(π(18 in))=(0.01227 in2)(π(18 in))=(0.694 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=4.016×10−4 ft3

Substitute 4.016×10−4 ft3 for V2, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (VI).

m2=(490 lb/ft332.2 ft/s2)(4.016×10−4 ft3)=(15.217 lb⋅s2/ft4)(4.016×10−4 ft3)=6.1112×10−3 lb⋅s2/ft

Substitute 18 in for d1 and 18 in for d in Equation (IX).

V3=(π4(18 in)2)(18 in)=(0.01227 in2)(18 in)=(0.22086 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=1.2783×10−4 ft3

Substitute 1.2783×10−4 ft3 for V3, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (VIII).

m3=(490 lb/ft332.2 ft/s2)(1.2783×10−4 ft3)=(15.217 lb⋅s2/ft4)(1.2783×10−4 ft3)=1.945×10−3 lb⋅s2/ft

Substitute 18 in for d1 and 18 in for d in Equation (XI).

V4=(π4(18 in)2)(18 in)=(0.01227 in2)(18 in)=(0.22086 in3)(1 ft12 in)(1 ft12 in)(1 ft12 in)=1.2783×10−4 ft3

Substitute 1.2783×10−4 ft3 for V4, 490 lb/ft3 for γST and 32.2 ft/s2 for g in Equation (X).

m4=(490 lb/ft332.2 ft/s2)(1.2783×10−4 ft3)=(15.217 lb⋅s2/ft4)(1.2783×10−4 ft3)=1.945×10−3 lb⋅s2/ft

Substitute 6.1112×10−3 lb⋅s2/ft for m1 and 18 in for d in Equation (XIII).

(Ix)1=12(6.1112×10−3 lb⋅s2/ft)(18 in)2=12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=12(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=6.8751×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m2 and 18 in for d in Equation (XIV).

(Ix)2=12(6.1112×10−3 lb⋅s2/ft)(18 in)2+(6.1112×10−3 lb⋅s2/ft)(18 in)2=[12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2]=(6.8751×10−3 ft⋅s2)+(13.7502×10−3 ft⋅s2)=20.6252×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m3 and 18 in for d in Equation (XV).

(Ix)3=[112(1.945×10−3 lb⋅s2/ft)(18 in)2+(1.945×10−3 lb⋅s2/ft){(18 in2)2+(18 in)2}]=[112(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(1.945×10−3 lb⋅s2/ft)[{(18 in2)(1 ft12 in)}2+{(18 in)(1 ft12 in)}2]]=(0.3647×10−3 lb⋅ft⋅s2)+(5.4712×10−3 lb⋅ft⋅s2)=5.8359×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m4 and 18 in for d in Equation (XVI).

(Ix)4=[112(1.945×10−3 lb⋅s2/ft)(18 in)2+(1.945×10−3 lb⋅s2/ft){(18 in2)2+(18 in)2}]=[112(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(1.945×10−3 lb⋅s2/ft)[{(18 in2)(1 ft12 in)}2+{(18 in)(1 ft12 in)}2]]=(0.3647×10−3 lb⋅ft⋅s2)+(5.4712×10−3 lb⋅ft⋅s2)=5.8359×10−3 lb⋅ft⋅s2

Substitute 6.8751×10−3 lb⋅ft⋅s2 for (Ix)1, 20.6252×10−3 lb⋅ft⋅s2 for (Ix)2, 5.8359×10−3 lb⋅ft⋅s2 for (Ix)3 and 5.8359×10−3 lb⋅ft⋅s2 for (Ix)4 in Equation (XII).

Ix=[(6.8751×10−3 lb⋅ft⋅s2)+(20.6252×10−3 lb⋅ft⋅s2)+(5.8359×10−3 lb⋅ft⋅s2)+(5.8359×10−3 lb⋅ft⋅s2)]=(27.5003×10−3 lb⋅ft⋅s2)+(11.6718×10−3 lb⋅ft⋅s2)=39.1721×10−3 lb⋅ft⋅s2

Thus, the mass moment of inertia of the wire with respect to x axis is 39.1721×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m1 and 18 in for d in Equation (XVIII).

(Iy)1=(6.1112×10−3 lb⋅s2/ft)(18 in)2=(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=13.7502×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m2 and 18 in for d in Equation (XIX).

(Iy)2=(6.1112×10−3 lb⋅s2/ft)(18 in)2=(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=13.7502×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m3 and 18 in for d in Equation (XX).

(Iy)3=(1.945×10−3 lb⋅s2/ft)(18 in)2=(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=4.3769×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m4 and 18 in for d in Equation (XXI).

(Iy)4=(1.945×10−3 lb⋅s2/ft)(18 in)2=(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=4.3769×10−3 lb⋅ft⋅s2

Substitute 13.7502×10−3 lb⋅ft⋅s2 for (Iy)1, 13.7502×10−3 lb⋅ft⋅s2 for (Iy)2, 4.3769×10−3 lb⋅ft⋅s2 for (Ix)3 and 4.3769×10−3 lb⋅ft⋅s2 for (Ix)4 in Equation (XVII).

Iy=[(13.7502×10−3 lb⋅ft⋅s2)+(13.7502×10−3 lb⋅ft⋅s2)+(4.3769×10−3 lb⋅ft⋅s2)+(4.3769×10−3 lb⋅ft⋅s2)]=(27.5004×10−3 lb⋅ft⋅s2)+(8.7538×10−3 lb⋅ft⋅s2)=36.2542×10−3 lb⋅ft⋅s2

Thus, the mass moment of inertia of the wire with respect to y axis is 36.2542×10−3 lb⋅ft⋅s2.

Substitute 6.1112×10−3 lb⋅s2/ft for m1 and 18 in for d in Equation (XXIII).

(Iz)1=12(6.1112×10−3 lb⋅s2/ft)(18 in)2=12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=12(6.1112×10−3 lb⋅s2/ft)(2.25 ft2)=6.8751×10−3 lb⋅ft⋅s2

Substitute 6.1112×10−3 lb⋅s2/ft for m2 and 18 in for d in Equation (XXIV).

(Iz)2=12(6.1112×10−3 lb⋅s2/ft)(18 in)2+(6.1112×10−3 lb⋅s2/ft)(18 in)2=[12(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2+(6.1112×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2]=(6.8751×10−3 ft⋅s2)+(13.7502×10−3 ft⋅s2)=20.6252×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m3 and 18 in for d in Equation (XXV).

(Iz)3=13(1.945×10−3 lb⋅s2/ft)(18 in)2=13(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=1.4590×10−3 lb⋅ft⋅s2

Substitute 1.945×10−3 lb⋅s2/ft for m4 and 18 in for d in Equation (XXVI).

(Iz)4=13(1.945×10−3 lb⋅s2/ft)(18 in)2=13(1.945×10−3 lb⋅s2/ft){(18 in)(1 ft12 in)}2=1.4590×10−3 lb⋅ft⋅s2

Substitute 6.8751×10−3 lb⋅ft⋅s2 for (Iz)1, 20.6252×10−3 lb⋅ft⋅s2 for (Iz)2, 1.4590×10−3 lb⋅ft⋅s2 for (Iz)3 and 1.4590×10−3 lb⋅ft⋅s2 for (Iz)4 in Equation (XXII).

Iz=[(6.8751×10−3 lb⋅ft⋅s2)+(20.6252×10−3 lb⋅ft⋅s2)+(1.4590×10−3 lb⋅ft⋅s2)+(1.4590×10−3 lb⋅ft⋅s2)]=(27.5003×10−3 lb⋅ft⋅s2)+(3.098×10−3 lb⋅ft⋅s2)=30.5983×10−3 lb⋅ft⋅s2

Thus, the mass moment of inertia of the wire with respect to z axis is 30.5983×10−3 lb⋅ft⋅s2

Conclusion:

The mass moment of inertia of the wire with respect to x axis is 39.1721×10−3 lb⋅ft⋅s2.

The mass moment of inertia of the wire with respect to y axis is 36.2542×10−3 lb⋅ft⋅s2.

The mass moment of inertia of the wire with respect to z axis is 30.5983×10−3 lb⋅ft⋅s2

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

7) find the Emax for figure below. 250N Ans: Tmay 7.5 MPa Gomm 350mm 50mm 4

Water is supplied at 150 ft³/s and 70 psi to a hydraulic turbine through a 3-ft inside-diameter inlet pipe as indicated in the figure below. The turbine discharge pipe has a 4.8-ft inside diameter. The static pressure at section (2), 10 ft below the turbine inlet, is 10 in. Hg vacuum. If the turbine develops 2400 hp, determine the rate of loss of available energy between sections (1) and (2). Section (1) P₁ =70psi Q=150ft³/s D₁ = 3 ft 10 ft Turbine power loss = i P₂ = 10 in. Hg vacuum D₂ =4.8ft Section (2) de hp

This problem studies the response of two single degree of freedom bridge systems shown in Figure 1 under three loading cases. The problem has two parts. Part A and Part B use the same loading cases but the system is modified. Assume the following three loading cases in both Part A and Part B: (a) Harmonic wind load acting on the bridge deck pw(t) = powsin(ωwt) with amplitude pow and forcing circular frequency ωw. (b) Harmonic displacement base excitation acting at the base of the bridge pier ug(t) = ugosin(ωgt) with amplitude ugo and displacement circular frequency ωg. (c) Rectangular pulse load acting on the bridge deck with amplitude pop and pulse duration td. Part A The system includes part of a bridge deck and a bridge pier shown in Figure 1(a). For each loading case find the symbolic expression of the peak shear force in the bridge pier assuming the following: • The bridge deck is rigid and it has a mass m. • The bridge deck is rigidly connected with the bridge pier (i.e.,…

Answer 2