
Concept explainers
For the beam and loading shown, determine (a) the slope at point B, (b) the deflection at point D. Use E = 200 GPa.
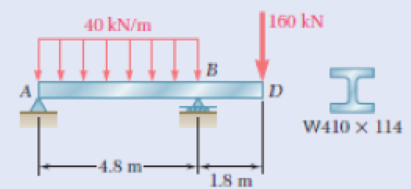
Fig. P9.128
The magnitude
Answer to Problem 146P
The magnitude
Explanation of Solution
Given information:
The section of the beam is
The young’s modulus of steel is
Calculation:
Show the free body diagram of the beam as in Figure 1.
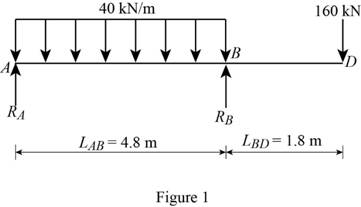
Calculate the vertical reaction at point A by taking moment about point B.
Refer Appendix C “Properties of rolled steel shape (SI units)” for moment of inertia of section
Calculate the value (EI):
Substitute
Calculate the moment due to the reaction at A:
Substitute
Calculate the
Substitute
Show the
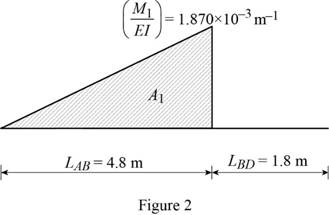
Calculate the area
Substitute
Calculate the moment due UDL:
Substitute
Calculate the
Substitute
Show the
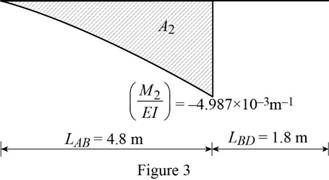
Calculate the area
Substitute
Calculate the moment due to the point load at D as below:
Substitute
Calculate the
Substitute
Show the
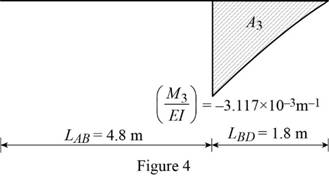
Calculate the area
Substitute
Calculate the tangential deviation of B with respect to A using the relation:
Substitute
Calculate the slope
Substitute
Let point K is the maximum deflection.
Calculate the moment due to the reaction at A as below:
Substitute
Calculate the
Substitute
Calculate the moment due UDL:
Calculate the
Substitute
Show the
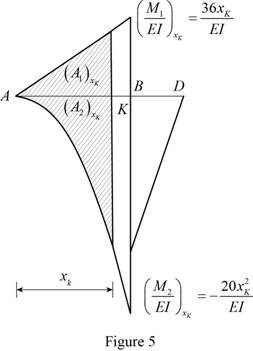
Calculate the area
Substitute
Calculate the area
Substitute
Calculate the slope
Substitute
Differentiate the Equation (1).
Solve the value
Iteration 1:
Substitute 3 for
Substitute 3 for
Iteration 2:
Calculate the value
Substitute 3 for
Similarly calculate the value
| f | ||
| 3 | 28.08 | -72 |
| 3.39 | -6.78 | -107.8 |
| 3.327 | -0.188 | -101.6 |
| 3.3251 | 0.005 | -101.42 |
| 3.32514 | 0.0001 |
The value of
Calculate the slope at the end A related to the point K
Substitute
Calculate the magnitude
Substitute
Thus, the magnitude
Want to see more full solutions like this?
Chapter 9 Solutions
EBK MECHANICS OF MATERIALS
- calculate their DoF using Gruebler's formula. PUNTO 6. PUNTO 7. (Ctrl)arrow_forwardA pump delivering 230 lps of water at 30C has a 300-mm diameter suction pipe and a 254-mm diameter discharge pipe as shown in the figure. The suction pipe is 3.5 m long and the discharge pipe is 23 m long, both pipe's materials are cast iron. The water is delivered 16m above the intake water level. Considering head losses in fittings, valves, and major head loss. a) Find the total dynamic head which the pump must supply. b)It the pump mechanical efficiency is 68%, and the motor efficiency is 90%, determine the power rating of the motor in hp.given that: summation of K gate valve = 0.25check valve=390 degree elbow= 0.75foot valve= 0.78arrow_forwardA pump delivering 230 lps of water at 30C has a 300-mm diameter suction pipe and a 254-mm diameter discharge pipe as shown in the figure. The suction pipe is 3.5 m long and the discharge pipe is 23 m long, both pipe's materials are cast iron. The water is delivered 16m above the intake water level. Considering head losses in fittings, valves, and major head loss. a) Find the total dynamic head which the pump must supply. b)It the pump mechanical efficiency is 68%, and the motor efficiency is 90%, determine the power rating of the motor in hp.arrow_forward
- The tensile 0.2 percent offset yield strength of AISI 1137 cold-drawn steel bars up to 1 inch in diameter from 2 mills and 25 heats is reported as follows: Sy 93 95 101 f 97 99 107 109 111 19 25 38 17 12 10 5 4 103 105 4 2 where Sy is the class midpoint in kpsi and fis the number in each class. Presuming the distribution is normal, determine the yield strength exceeded by 99.0% of the population. The yield strength exceeded by 99.0% of the population is kpsi.arrow_forwardSolve this problem and show all of the workarrow_forwardI tried to go through this problem but I don't know what I'm doing wrong can you help me?arrow_forward
- Generate the kinematic diagram of the following mechanisms using the given symbols. Then, draw their graphs and calculate their degrees of freedom (DoF) using Gruebler's formula. PUNTO 2. PUNTO 3. !!!arrow_forwardCreate a schematic representation of the following mechanisms using the given symbols and draw their graphs. Then, calculate their degrees of freedom (DoF) using Gruebler's formula. PUNTO 6. PUNTO 7.arrow_forwardhow the kinematic diagram of the following mechanisms would be represented using the given symbols? PUNTO 0. PUNTO 1. °arrow_forward
- Create a schematic representation of the following mechanisms using the given symbols and draw their graphs. Then, calculate their degrees of freedom (DOF) using Gruebler's formula. PUNTO 4. PUNTO 5. (0) Groundarrow_forwardDraw the graph of ALL the mechanisms and calculate their DoF using Gruebler's formula. PUNTO 0. PUNTO 1.arrow_forwardAn adjustable support. Construction designed to carry vertical load and is adjusted by moving the blue attachment vertically. The link is articulated at both ends (free to rotate) and can therefore only transmit power axially. Analytically calculate the force to which the link is subjected? Calculate analytically rated voltage in the middle of the link.? F=20kN Alpha 30 deg Rel 225 Mpans:5arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





