
Concept explainers
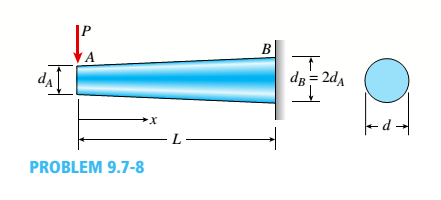
The tapered cantilever beam AB shown in the figure has a solid circular cross section. The diameters at the ends A and B are dAand dB= 2dA, respectively. Thus, the diameter d and moment of inertia / at distance v from the free end are, respectively,
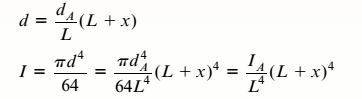 in which IAis the moment of inertia at end A of the beam.
in which IAis the moment of inertia at end A of the beam.
Determine the equation of the deflection curve and the deflection SAat the free end of the beam due to the load P.
The equation for the deflection curve and the deflection
Answer to Problem 9.7.8P
The equation for the deflection curve and the deflection
Explanation of Solution
Given Information:
We have,
Length of the tapered cantilever beam AB, L
Load at point A as P
Diameter at point A,
Diameter at point B,
Moment of inertia, I
The bending moment is
So, the 2nd degree diffrential equation would be,
In the above equation, taking integration on both sides :
According to boundary condition at x=L,
In above equation taking integration again,
And at 2nd Boundary conditions, x = L and v = 0.
At x = 0, then
At point A, the deflection would be below.
Conclusion:
The answers are calculated according to deflection and deflection curve.
Want to see more full solutions like this?
Chapter 9 Solutions
Mechanics of Materials (MindTap Course List)
- Access Pearson Mastering Engineering Back to my courses Course Home Course Home Scoresarrow_forwardAccess Pearson Mastering Engineering Back to my courses Course Home Course Home Scores Review Next >arrow_forwardAccess Pearson Course Home Scoresarrow_forwardCan you answer this question?arrow_forwardCan you answer this question?arrow_forwardA gear has a gear wheel with 16 teeth. The gear should be dimensioned for the highest and lowest gear ratio. Looking for output power, torque, speed?nin= 2000 rpmmin = 30Nmn=0,9a max= 450 mmModule 4Gear limitsz1 z213 13-1614 14-2615 15-4516 16-10117 17-131418 18-…..I have calculate but I can’t get the right answers…..√16 =459x60/56x57=1.1 lowest59x60/13x13=20,94 highestnut=2000/1.1= 1818rpmnut=2000/20.94=95.5 rpmMut=1.1x30=33 NmMut=20.94x30=628,2 Nm(Right answer)LowestZ=13, M=24,4Nm, n=2462 rpmHighestZ=92, M=172,5Nm, n=347,8 rpmP=5655W on botharrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
