Chapter 9, Problem 9.7.12P

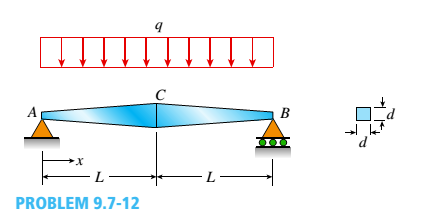
A simple beam ACE is constructed with square cross sections and a double taper (see figure). The depth of the beam at the supports is d_Aand at the midpoint is d_c= 2d ₄. Each half of the beam has length L. Thus, the depth and moment of inertia / at distance x from the left-hand end are, respectively, in which I_Ais the moment of inertia at end A of the beam. (These equations are valid for .x between 0 and L, that is, for the left-hand half of the beam.)

1. Obtain equations for the slope and deflection of the left-hand half of the beam due to the uniform load.

From the equations in part (a), obtain formulas for the angle of rotation 9₄at support A and the deflection S_cat the midpoint.

  

To determine

The equations for the slope and deflection of the left-hand half of the beam for the given simple beam due to uniform load.

Answer to Problem 9.7.12P

The equation for the slope and deflection of the left-hand half of the beam are:$\frac{dv}{dx}=-\frac{q{L}^3}{16E{I}_A}\left[1-\frac{8L{x}^2}{{\left(L+x\right)}^3}\right]0\le x\le L$ , and$v=-\frac{q{L}^3}{16E{I}_A}\left[x-\frac{4L^2\left(3L+4x\right)}{(L+x^2)}-8L\ln (L+x)\right]+c_2$ for a simple beam ACB.

Explanation of Solution

Given: .

We have,

Length of the beam, AB =2L..

Depth of the beam at support,$d_A.$.

Depth of the beam at midpoint,$d_c=2d_A.$.

Moment of inertia, I

Depth at the left-hand end,$d=\frac{d_A}{L}\left(L+x\right).$.

Concept Used: .

Annuity problem requires the use of the differential equation as follows:.

  $\begin{array}{l}\frac{dp}{dt}=r(p(t)-\frac{N}{r})N=\text{Withdrawal Rate, }P=\text{Deposit, }r=\text{Interest rate}\\ \Rightarrow \frac{dp}{(p-\frac{N}{r})}=rdt\\ \text{on integration we get}\\ \ln (p-\frac{N}{r})=rt+\ln c\\ \Rightarrow \ln (\frac{p-\frac{N}{r}}{c})=rt\\ \Rightarrow (p-\frac{N}{r})=c{e}^{rt}\\ \Rightarrow p(t)=\frac{N}{r}+c{e}^{rt}\end{array}$.

Calculation: .

With the use of we can calculate,

$\begin{array}{l}I=\frac{d^4}{12}\\ I=\frac{{\left(\frac{d_A}{L}\left(L+x\right)\right)}^4}{12}\\ I=\frac{d_A{}^4}{12L^4}{\left(L+x\right)}^4\\ I=\frac{\left(\frac{d_A{}^4}{12}\right)}{L^4}{\left(L+x\right)}^4\\ I=\frac{I_A{}^4}{L^4}{\left(L+x\right)}^{4}0\le x\le L\end{array}$.

The reaction forces at point A and B would be,

$R_A=qL{\text{ and R}}_B=qL$.

The bending moment would be,

$\begin{array}{l}M=R_{A}x-\frac{q{x}^2}{2}\\ M=qLx-\frac{q{x}^2}{2}\end{array}$.

Now we are using second degree differential eqaution as follow,

$\begin{array}{l}EI\frac{d^{2}v}{d{x}^2}=M\\ EI\frac{d^{2}v}{d{x}^2}=qLx-\frac{q{x}^2}{2}\\ \frac{d^{2}v}{d{x}^2}=\frac{1}{EI}\left(qLx-\frac{q{x}^2}{2}\right)\\ \frac{d^{2}v}{d{x}^2}=\frac{1}{E\left(\frac{I_A{}^4}{L^4}\right){\left(L+x\right)}^4}\left(qLx-\frac{q{x}^2}{2}\right)\\ \frac{d^{2}v}{d{x}^2}=\frac{L^4}{E{I}_A{}^4}\left(qL\frac{x}{{\left(L+x\right)}^4}-\frac{q}{2}\frac{x^2}{{\left(L+x\right)}^4}\right)\end{array}$.

In the above equation taking integration at both sides,

  $\begin{array}{l}\frac{d^{2}v}{d{x}^2}=\frac{L^4}{E{I}_A{}^4}\left(qL\frac{x}{{\left(L+x\right)}^4}-\frac{q}{2}\frac{x^2}{{\left(L+x\right)}^4}\right)\\ \frac{dv}{dx}=\frac{L^4}{E{I}_A}\left(qL\left(\frac{-\left(L+3x\right)}{6{\left(L+x\right)}^3}\right)+\frac{q}{2}\left(\frac{L^2+3Lx+3x^2}{3{\left(L+x\right)}^3}\right)\right)+c_1\end{array}$.

The boundary conditions at x =L..

  $\begin{array}{l}\frac{dv}{dx}=\frac{L^4}{E{I}_A}\left(qL\left(\frac{-\left(L+3x\right)}{6{\left(L+x\right)}^3}\right)+\frac{q}{2}\left(\frac{L^2+3Lx+3x^2}{3{\left(L+x\right)}^3}\right)\right)+c_1\\ \frac{dv}{dx}=0\\ 0=\frac{L^4}{E{I}_A}\left(qL\left(\frac{-\left(L2+3x\right)}{6{\left(L+x\right)}^3}\right)+\frac{q}{2}\left(\frac{L^2+3Lx+3x^2}{3{\left(L+x\right)}^3}\right)\right)+c\\ c_1=\frac{-q{L}^3}{16E{I}_A}\\ So,\\ \frac{dv}{dx}=\frac{q{L}^4{x}^2}{2E{I}_A{\left(L+x\right)}^3}-\frac{q{L}^3}{16E{I}_A}\\ \frac{dv}{dx}=-\frac{q{L}^3}{16E{I}_A}\left[1-\frac{8L{x}^2}{{\left(L+x\right)}^3}\right]0\le x\le L\end{array}$.

In the above equation, Once again taking integration, we will get,

  $\begin{array}{l}\frac{dv}{dx}=-\frac{q{L}^3}{16E{I}_A}\left[1-\frac{8L{x}^2}{{\left(L+x\right)}^3}\right]\\ v=-\frac{q{L}^3}{16E{I}_A}\left[x-8L\frac{L\left(3L+4x\right)}{2(L+x^2)}-8L\ln (L+x)\right]+c_2\\ v=-\frac{q{L}^3}{16E{I}_A}\left[x-\frac{4L^2\left(3L+4x\right)}{(L+x^2)}-8L\ln (L+x)\right]+c_2\end{array}$.

Conclusion: .

The balance in the annuity after$10$ years$=\mathrm{17563.9365.}$

To determine

The formulas for the angle of rotation at the support and the deflection at the midpoint with the use of equations found in part (a).

Answer to Problem 9.7.12P

The equation for the angle of rotation${\theta }_A$ at support A and the deflection${\delta }_C$ at midpoint are,${\theta }_A=\frac{q{L}^3}{16E{I}_A}$ and${\delta }_c=0.028426\frac{q{L}^4}{E{I}_A}$for a simple beam ACB.

Explanation of Solution

Given: .

We have,

Length of the beam, AB =2L..

Depth of the beam at support,$d_A.$.

Depth of the beam at midpoint,$d_c=2d_A.$.

Moment of inertia is I..

Depth at the left-hand end,$d=\frac{d_A}{L}\left(L+x\right).$.

Concept Used: .

Annuity problem requires the use of the differential equation as follows:.

  $\begin{array}{l}\frac{dp}{dt}=r(p-\frac{N}{r})N=\text{Withdrawal Rate, }P=\text{Deposit Amount, }r=\text{interest rate}\\ \Rightarrow \frac{dp}{(p-\frac{N}{r})}=rdt\\ \text{on integration we get}\\ \ln (p-\frac{N}{r})=rt+\ln c\\ \Rightarrow \ln (\frac{p-\frac{N}{r}}{c})=rt\\ \Rightarrow (p-\frac{N}{r})=c{e}^{rt}\\ \Rightarrow p(t)=\frac{N}{r}+c{e}^{rt}\end{array}$.

Calculation: .

We have the equation,

  $v=-\frac{q{L}^4}{2E{I}_A}\left[\frac{9L^2+14Lx+x^2}{8L{(L+x)}^2}-\ln \left(1+\frac{x}{2}\right)\right]$.

On this above equation, boundary condition at x =0 and v =0..

  $\begin{array}{l}0=\frac{q{L}^3}{16E{I}_A}\left[\frac{12L^3}{L^2}+8L\ln L\right]+c_2\\ c_2=\frac{-q{L}^3}{16E{I}_A}\left[\frac{12L^3}{L^3}+8L\ln L\right]+c_2\\ c_2=\frac{-q{L}^4}{2E{I}_A}\left[\frac{3}{2}+\ln L\right]\end{array}$.

  $\begin{array}{l}\text{Angle of rotation at point A,}\\ {\theta }_A=-{\left(\frac{dv}{dx}\right)}_{x=0}\\ {\theta }_A=\frac{q{L}^3}{16E{I}_A}\end{array}$.

So, deflection beam would be,

  $\begin{array}{l}v=-\frac{q{L}^3}{16E{I}_A}\left[x-\frac{8L^2\left(-3L+4x\right)}{2{(L+x)}^2}-8L\ln (L+x)\right]-\frac{q{L}^4}{2E{I}_A}\left[\frac{3}{2}+\ln L\right]\\ v=-\frac{q{L}^3}{2E{I}_A}\left[\frac{x}{8}+\frac{L^2\left(3L+4x\right)}{2{(L+x)}^2}+L\ln (L+x)+\frac{3}{2}+\ln L\right]\\ v=-\frac{q{L}^4}{2E{I}_A}\left[\frac{9L^2+14Lx+x^2}{8L{(L+x)}^2}-\ln \left(1+\frac{x}{2}\right)\right]\end{array}$.

Deflection at,

  $\begin{array}{l}{c}_1{\delta }_c=-v_{x=L}\\ {\delta }_c=\frac{q{L}^4}{8E{I}_A}\left(3-4\ln 2\right)\\ {\delta }_c=\frac{q{L}^4}{8E{I}_A}\left(0.2274\right)\\ {\delta }_c=0.028426\frac{q{L}^4}{E{I}_A}\end{array}$.

Conclusion: .

The equation for the angle of rotation${\theta }_A$ at support A and the deflection${\delta }_C$ at midpoint are,${\theta }_A=\frac{q{L}^3}{16E{I}_A}$ and${\delta }_c=0.028426\frac{q{L}^4}{E{I}_A}$for a simple beam ACB.