Chapter 9, Problem 9.5.1P

To determine

(a)

Use LFRD method to select the $\text{W}16X$ satisfactory shape.

Answer to Problem 9.5.1P

$\text{W}16X31$

Explanation of Solution

Given:

Thickness of slab, t = 4.5 inches, spacing = 6.5 ft, span length, L = 36 feet, yield stress = 50 Ksi

Construction load = 20 psf, and live load = 175 psf.

The value of $f_{{}_c}^{\text{'}}=4ksi$.

Concept Used:

Calculation:

Using LRFD method, we have

To select the suitable W 16 shape as follows:

Calculate the loads on the beam as follows:

After curing we have,

$W_S=\frac{t}{12}(150)L_p$

Where, $t$ is the thickness of the slab, $W_S$ the self-weight of slab on one beam, $L_p$ is the distance

between two adjacent beams.

$W_S=\frac{t}{12}(150)L_p$

$\begin{array}{l}{W}_S=\frac{4.5}{12}(150)\times 6.5\\ W_S=365.625\frac{lb}{ft}.\end{array}$

The dead load on the beam after the concrete has cured is:

$W_D=W_S$

Where, $W_D$ is the dead load on the beam.

Neglecting the beam weight and check for it later.

$W_D=W_S=365.625\frac{lb}{ft}$

Calculate the live load on the beam using the following equation:

$W_D=W_{{}_{SL}}{L}_P$

Where, $W_{SL}$ is the construction load on the beam.

$\begin{array}{l}{W}_D=W_{{}_{SL}}{L}_P\\ W_D=175psf\times 6.5ft\\ W_D=1137.5\frac{lb}{ft}\\ W_D=1138\frac{lb}{ft}\end{array}$

Calculate the factored uniformly distributed load after curing has completed by the following formula:

$W_u=\left(\left(1.2\times W_D\right)+\left(1.6\times W_L\right)\right)\frac{Kips}{ft}$

Where, $W_D$ is the uniformly distributed dead load on the beam and $W_L$ is the applied live load on the beam.

Substitute the values, we get

$\begin{array}{l}{W}_u=\left(\left(1.2\times W_D\right)+\left(1.6\times W_L\right)\right)\frac{Kips}{ft}\\ W_u=\left(\left(1.2\times 0.3656\right)+\left(1.6\times 1.138\right)\right)\frac{Kips}{ft}\\ W_u=2.2595\frac{Kips}{ft}\\ W_u=2.26\frac{Kips}{ft}\end{array}$

Calculate the bending moment on the beam;

$M_u=\frac{w_u{L}_{AB}^2}{8}$

Where, $M_u$ is the bending moment and $L_{AB}^{}$ is the length of the beam.

$\begin{array}{l}{M}_u=\frac{w_u{L}_{AB}^2}{8}\\ M_u=\frac{\left(2.26\times {36}^2\right)}{8}\frac{Kips}{ft}f{t}^2\\ M_u=366.1Kips\text{-}ft.\end{array}$

Let’s try a 16-inch deep beam.

Select a shape with the limiting self-weight given by the following formula:

$W=\frac{3.4M_u}{\varphi F_Y\left[\frac{d}{2}+t-\frac{a}{2}\right]}$

Where, t is the thickness of the concrete slab, d is the depth of the steel beam, a is the distance of the neutral axis from the top, $F_Y$ is the yield strength of steel and $\varphi$ is the reduction factor.

Estimating weight per unit foot of the steel beam as:

$\begin{array}{l}W=\frac{3.4M_u}{\varphi F_Y\left[\frac{d}{2}+t-\frac{a}{2}\right]}\\ W=\frac{3.4\times 366.1Kips\text{-}ft}{0.9\times 50Ksi\left[\frac{16inch}{2}+4.5inch-\frac{1inch}{2}\right]}\\ W=27.66\frac{lb}{ft}.\end{array}$

Let’s try for W 16 X 31 and note the properties and dimensions from the Manual.

Calculate the strength of the section as following below:

$C=\min (C_C,C_S)$

Where, the compressive force is C, the compressive force of concrete is $C_C$, and the compressive force of steel beam is $C_S$.

Calculate the compressive force in steel as follows:

$C_S=A_S{F}_Y$

Where, the area of steel section is $A_S$ and the yield strength of steel is $F_Y$

Get the value of $A_S$ from properties and dimensions table from part 1 of the manual.

$A_S=9.13inche{s}^2.$

$\begin{array}{l}{C}_S=9.13inche{s}^2\times 50Ksi\\ C_S=456.5Kips.\end{array}$

Calculate the compressive force in concrete as following:

$C_C=0.85f_C^{\text{'}}bt$

Where, b is the width of the concrete slab, t is the thickness of the concrete beam and $f_C^{\text{'}}$ is the compressive strength of the concrete.

The effective flange width is as follows:

$\begin{array}{l}b=\text{Min}\left(\frac{12L_{AB}}{t},12L_p\right)\\ b=\text{Min}\left(\frac{12\times 36}{4},12\times 6.5\right)\\ b=\text{Min}\left(108in,78in\right)\\ b=78in.\end{array}$

Substitute the values in the above equation, we get

$\begin{array}{l}{C}_C=0.85\times 4ksi\times 78in\times 4.5in\\ C_C=1193.4kips.\end{array}$

Therefore, the compressive force is as follows:

$\begin{array}{l}C=\min (C_C,C_S)\\ C=\min (1193.4kips,456.5kips)\\ C=456.5kips.\end{array}$

Therefore, the plastic neutral axis lies in the slab.

Calculate the tensile force (T) and compressive force (C) and the position of plastic neutral axis from the top of concrete slab by following formula:

$C=T$

$\begin{array}{l}0.85f_C^{\text{'}}ab=A_S{F}_y\\ 0.85f_C^{\text{'}}ab=C\end{array}$

$\begin{array}{l}0.85\times 4Ksi\times a\times 78=456.5kips\\ a=1.721in\end{array}$

Compute the flexural strength as:

$M_n=Cy$

Where, $M_n$ is the flexural strength and y is the distance of action of tensile force from plastic

neutral axis.

Compute the value of Y as following below:

$\begin{array}{l}y=\frac{d}{2}+t-\frac{a}{2}\\ y=\frac{15.9in}{2}+4.5in-\frac{1.721in}{2}\\ y=7.95+4.50-0.8605\\ y=11.59in.\end{array}$

Substitute the values, we get

$M_n=Cy$

$\begin{array}{l}{M}_n=456.5Kips\times 11.59in\\ M_n=5290.835in-Kips\\ M_n=440.90ft-Kips\end{array}$

Calculate the design strength of the section as follows:

$M_d=\left({\varphi }_b\times M_n\right)$

Where, $M_d$ is the design strength of the beam.

Substitute the values, we get

$\begin{array}{l}{M}_d=\left({\varphi }_b\times M_n\right)\\ M_d=\left(0.90\times 441.1\right)Kips.ft\\ M_d=397Kips.ft\end{array}$

The flexural strength of the beam after curing is given as:

$\begin{array}{l}{M}_d=\left({\varphi }_b\times M_n\right)\\ =397Kips.ft\end{array}$

Where, $\left({\varphi }_b\times M_n\right)$ is the nominal flexural strength and $M_d$ is the design strength.

Comparing the values of $\left({\varphi }_b{M}_n\right)$ and $M_u$, We have

$\begin{array}{l}366.1Kips\text{-}ft<397Kips.ft\\ M_u<\left({\varphi }_b{M}_n\right)\end{array}$

Thus, the beam is satisfactory in bending after the curing of concrete is complete.

Check for beam weight.

Where, $W_S$ is the self-weight of the beam, $W_D$ is the uniformly distributed dead load on the beam and $W_L$ is the applied live load on the beam.

Substitute the values, we get

$\begin{array}{l}{W}_u=\left(1.2\left(W_S+W_D\right)+\left(1.6\times W_L\right)\right)\frac{Kips}{ft}\\ W_u=\left(\left(1.2\left(0.3656psf+0.031psf\right)\right)+\left(1.6\left(1.138psf\right)\right)\right)\frac{Kips}{ft}\\ W_u=0.4759\frac{Kips}{ft}+1.821\frac{Kips}{ft}\\ W_u=2.297\frac{Kips}{ft}\end{array}$

Calculate the maximum bending moment on the beam;

$M_{ul}=\frac{w_u{L}_{}^2}{8}$

Where, $M_{ul}$ is the maximum bending moment and $L_{}^{}$ is the length of the beam.

$\begin{array}{l}{M}_{ul}=\frac{w_u{L}_{}^2}{8}\\ M_{ul}=\frac{\left(2.297\times {36}^2\right)}{8}\frac{Kips}{ft}f{t}^2\\ M_{ul}=372Kips\text{-}ft.\end{array}$

Check the flexural strength of the beam.

Compare the maximum bending moment and the nominal flexural strength

Comparing the values of $\left({\varphi }_b{M}_n\right)$ and $M_{ul}$, We have

$\begin{array}{l}372Kips\text{-}ft<397Kips\text{-}ft\\ M_{ul}<\left({\varphi }_b{M}_n\right)\end{array}$

Thus, the section is safe in flexure including its self-weight.

Check for the shear:

Checking the value of nominal value of shear strength of $\text{W}16\text{×31}$ from the AISC Manual.

${\varphi }_v{V}_n=131\text{kips}$

Where, ${\varphi }_v{V}_n$ is the nominal shear strength.

The maximum shear force is as following for the above conditions:

$V_n=\frac{w_{u}L}{2}$

Substitute the values, we have

$\begin{array}{l}{V}_n=\frac{w_{u}L}{2}\\ V_n=\frac{2.297{\text{kips ft}}^{\text{-1}}\times 36\text{ft}}{2}\\ V_n=41.4\text{kips}\end{array}$

Now comparing the two we have

$V_n=41.4\text{kips}<{\varphi }_v{V}_n=131\text{kips}$

Therefore, the beam is safe in shear and we can use $\text{W}16\text{×31}$.

Calculate the factored uniformly distributed load after curing has completed by following formula:

$W_u=\left(\left(1.2\times W_D\right)+\left(1.6\times W_L\right)\right)\frac{Kips}{ft}$

Load before curing:

Calculate the self-weight of the slab to be allowed by a single beam as

$W_S=\frac{t}{12}(150)L_p$

Where, $t$ is the thickness of the slab, $L_p$ is the distance between two adjacent beams.

$\begin{array}{l}{W}_S=\frac{4.5}{12}(150)\times 6.5ft\\ W_S=365.6\frac{lb}{ft}.\end{array}$

The dead load on the beam before the concrete has cured

$W_d=\left(w+w_s\right)$

Where, w is the self-weight of the beam

Substitute the values, we have

$\begin{array}{l}{W}_d=\left(365.6+31\right)\frac{lb}{ft}\\ W_d=396.6\frac{lb}{ft}\end{array}$

Now, calculate the live load on the beam as follows

$W_L=\left(w_{sl}\right)L_p$

Where the construction load on the slab is $w_{sl}$

$\begin{array}{l}{W}_L=20psf\times 6.5ft\\ W_L=130\frac{lb}{ft}\end{array}$

The uniformly distributed factored load can be found as

$W_u=1.2W_d+1.6W_l$

Where, $W_d$ is the uniformly distributed dead load on the beam and applied live load on the beam is $W_l.$

Substitute the values in the above equation, we have

$\begin{array}{l}{W}_u=\left[1.2\times 0.3966\right]+\left[1.6\times 0.130\right]\\ W_u=0.47592+0.208\\ W_u=0.68392\frac{lb}{ft}\end{array}$

Calculate the maximum bending moment on the beam.

$M_{ul}=\frac{w_u{L}_{AB}^2}{8}$

Where, $M_{ul}$ is the maximum bending moment and $L_{AB}^{}$ is the length of the beam.

$\begin{array}{l}{M}_{ul}=\frac{w_u{L}_{AB}^2}{8}\\ M_{ul}=\frac{\left(0.6839\times {36}^2\right)}{8}\frac{Kips}{ft}f{t}^2\\ M_{ul}=110.80Kips\text{-}ft.\end{array}$

Check the value of the nominal flexural strength of W- sections from the Manual:

Flexural strength of the beam before curing is given as follows:

$\begin{array}{l}{\varphi }_b\times M_n={\varphi }_b\times M_P\\ =203Kips.ft\end{array}$

Where, $\left({\varphi }_b\times M_n\right)$ is the nominal flexural strength and ${\varphi }_b\times M_P$ is the plastic moment.

Comparing the values of $\left({\varphi }_b{M}_n\right)$ and $M_u$, We have

$\begin{array}{l}110.8Kips\text{-}ft<203Kips.ft\\ M_u<\left({\varphi }_b{M}_n\right)\end{array}$

Thus, the beam is satisfactory before the curing of concrete is complete.

Therefore, W 16 X 31 is satisfactory to use.

Conclusion:

Therefore, $\text{W}16X31$ is satisfactory to use.

To determine

(b)

Use ASD method to select the $\text{W}16X$ satisfactory shape.

Answer to Problem 9.5.1P

$\text{W}16X31$

Explanation of Solution

Calculation:

Applying Allowable stress design:

Select appropriate W 16 shape

Calculate the loads on the beam as follows:

Before curing

Calculate the self-weight of the slab to be allowed by a single beam as follows:

$W_S=\frac{t}{12}(150)L_p$

Where, $t$ is the thickness of the slab, $W_S$ the self-weight of slab on one beam, $L_p$ is the distance

between two adjacent beams.

$W_S=\frac{t}{12}(150)L_p$

$\begin{array}{l}{W}_S=\frac{4.5}{12}(150)\times 6.5\\ W_S=365.625\frac{lb}{ft}.\end{array}$

The dead load on the beam after the concrete has cured is:

$W_D=W_S$

Where, $W_D$ is the dead load on the beam.

Neglecting the beam weight and check for it later.

$W_D=W_S=365.625\frac{lb}{ft}$

Calculate the live load on the beam using the following equation:

$W_D=W_{{}_{SL}}{L}_P$

Where, $W_{SL}$ is the construction load on the beam.

$\begin{array}{l}{W}_D=W_{{}_{SL}}{L}_P\\ W_D=175psf\times 6.5ft\\ W_D=1137.5\frac{lb}{ft}\\ W_D=1138\frac{lb}{ft}\end{array}$

Calculate the allowable uniformly distributed load as follows:

$W_a=W_D+W_L$

Substitute the values as follows

$\begin{array}{l}{W}_a=0.3656\text{kips-ft}\text{+}1.138\text{kips-ft}\\ W_a=1.504\text{kips-ft}\end{array}$

Calculate the bending moment on the beam;

$M_u=\frac{w_u{L}_{AB}^2}{8}$

Where, $M_u$ is the bending moment and $L_{AB}^{}$ is the length of the beam.

$\begin{array}{l}{M}_u=\frac{w_u{L}_{AB}^2}{8}\\ M_u=\frac{\left(1.504\times {36}^2\right)}{8}\frac{Kips}{ft}f{t}^2\\ M_u=243.57Kips\text{-}ft.\end{array}$

Let’s try a 16-inch deep beam.

Select a shape with the limiting self-weight given by the following formula:

$W=\frac{3.4M_u}{\varphi F_Y\left[\frac{d}{2}+t-\frac{a}{2}\right]}$

Where, t is the thickness of the concrete slab, d is the depth of the steel beam, a is the distance of the neutral axis from the top, $F_Y$ is the yield strength of steel and $\varphi$ is the reduction factor.

Estimating weight per unit foot of the steel beam as:

$\begin{array}{l}W=\frac{3.4M_u}{\varphi F_Y\left[\frac{d}{2}+t-\frac{a}{2}\right]}\\ W=\frac{3.4\times 366.1Kips\text{-}ft}{0.9\times 50Ksi\left[\frac{16inch}{2}+4.5inch-\frac{1inch}{2}\right]}\\ W=27.66\frac{lb}{ft}.\end{array}$

Let’s try for W 16 X 31 and note the properties and dimensions from the Manual.

Calculate the strength of the section as following below:

$C=\min (C_C,C_S)$

Where, the compressive force is C, the compressive force of concrete is $C_C$, and the compressive force of steel beam is $C_S$.

Calculate the compressive force in steel as follows:

$C_S=A_S{F}_Y$

Where, the area of steel section is $A_S$ and the yield strength of steel is $F_Y$

Get the value of $A_S$ from properties and dimensions table from part 1 of the manual.

$A_S=9.13inche{s}^2.$

$\begin{array}{l}{C}_S=9.13inche{s}^2\times 50Ksi\\ C_S=456.5Kips.\end{array}$

Calculate the compressive force in concrete as following:

$C_C=0.85f_C^{\text{'}}bt$

Where, b is the width of the concrete slab, t is the thickness of the concrete beam and $f_C^{\text{'}}$ is the compressive strength of the concrete.

The effective flange width is as follows;

$\begin{array}{l}b=\text{Min}\left(\frac{12L_{AB}}{t},12L_p\right)\\ b=\text{Min}\left(\frac{12\times 36}{4},12\times 6.5\right)\\ b=\text{Min}\left(108in,78in\right)\\ b=78in.\end{array}$

Substitute the values in the above equation, we get

$\begin{array}{l}{C}_C=0.85\times 4ksi\times 78in\times 4.5in\\ C_C=1193.4kips.\end{array}$

Therefore, the compressive force is as follows:

$\begin{array}{l}C=\min (C_C,C_S)\\ C=\min (1193.4kips,456.5kips)\\ C=456.5kips.\end{array}$

Therefore, the plastic neutral axis lies in the slab.

Calculate the tensile force (T) and compressive force (C) and the position of plastic neutral axis from the top of concrete slab by following formula:

$C=T$

$\begin{array}{l}0.85f_C^{\text{'}}ab=A_S{F}_y\\ 0.85f_C^{\text{'}}ab=C\end{array}$

$\begin{array}{l}0.85\times 4Ksi\times a\times 78=456.5kips\\ a=1.721in\end{array}$

Compute the flexural strength as:

$M_n=Cy$

Where, $M_n$ is the flexural strength and y is the distance of action of tensile force from plastic

neutral axis.

Compute the value of Y as following below:

$\begin{array}{l}y=\frac{d}{2}+t-\frac{a}{2}\\ y=\frac{15.9in}{2}+4.5in-\frac{1.721in}{2}\\ y=7.95+4.50-0.8605\\ y=11.59in.\end{array}$

Substitute the values, we get

$M_n=Cy$

$\begin{array}{l}{M}_n=456.5Kips\times 11.59in\\ M_n=5290.835in-Kips\\ M_n=440.90ft-Kips\end{array}$

Calculate the design strength of the section as follows:

$M_d=\frac{M_n}{{\Omega }_b}$

Where, $M_d$ is the design strength of the beam.

Substitute the values, we get

$\begin{array}{l}{M}_d=\frac{M_n}{{\Omega }_b}\\ M_d=\frac{440.90}{1.67}Kips.ft\\ M_d=264Kips.ft\end{array}$

Check the nominal value of the flexural strength of W- sections from the manual.

$\begin{array}{l}{M}_d=\frac{M_n}{{\Omega }_b}\\ M_d=264\text{Kips}\text{.ft}\end{array}$

Where, $\frac{M_n}{{\Omega }_b}$ is the allowable flexural strength.

Comparing the values, we get

$\begin{array}{l}243.6\text{Kips}\text{.ft}<264\text{Kips}\text{.ft}\\ M_a<\frac{M_n}{{\Omega }_b}.\end{array}$

Thus, the beam is satisfactory after curing of concrete has completed.

Check for beam weight

Calculating the max bending mo0ment by busing the following formula:

$M_{al}=M_a+W_a\frac{L^2}{8}$

Substitute the values as follows:

$\begin{array}{l}{M}_{al}=M_a+W_a\frac{L^2}{8}\\ M_{al}=243.6Kipsft+0.031Kipsft\frac{{\left[36ft\right]}^2}{8}\\ M_{al}=243.6Kipsft+5.022Kipsft.\\ M_{al}=248.6Kipsft.\end{array}$

Now, checking the flexural strength with the beam taken into consideration:

Compare the maximum bending moment and the nominal flexural strength

Comparing the values of $\frac{M_n}{{\Omega }_b}$ and $M_u$, We have

$\begin{array}{l}248.6Kips\text{-}ft<264Kips\text{-}ft\\ M_u<\frac{M_n}{{\Omega }_b}\end{array}$

Thus, the section is safe in flexure including its self-weight.

Check for the shear:

Checking the value of nominal value of shear strength of $\text{W}16\text{×31}$ from the AISC Manual.

$\frac{V_n}{{\Omega }_v}=87.5\text{kips}$

Where, $\frac{V_n}{{\Omega }_v}$ is the nominal shear strength.

The maximum shear force is as following for the above conditions:

$V_a=\frac{\left(w_a+w\right)L}{2}$

Substitute the values, we have

$\begin{array}{l}{V}_a=\frac{\left(w_a+w\right)L}{2}\\ V_n=\frac{\left(1.504+0.031\right){\text{kips ft}}^{\text{-1}}\times 36\text{ft}}{2}\\ V_n=27.6\text{kips}\end{array}$

Now comparing the two we have

$V_a=27.6\text{kips}<\frac{V_n}{{\Omega }_v}=87.5\text{kips}$

Therefore, the beam is safe in shear.

Loading before curing:

Calculate the self-weight of the slab to be allowed by a single beam as follows:

$W_S=\frac{t}{12}(150)L_p$

Where, $t$ is the thickness of the slab, $W_S$ the self-weight of slab on one beam, $L_p$ is the distance

between two adjacent beams.

$W_S=\frac{t}{12}(150)L_p$

$\begin{array}{l}{W}_S=\frac{4.5}{12}(150)\times 6.5\\ W_S=365.625\frac{lb}{ft}.\end{array}$

The dead load on the beam before the concrete has cured

$W_d=\left(w+w_s\right)$

Where, w is the self-weight of the beam

Substitute the values, we have

$\begin{array}{l}{W}_d=\left(365.6+31\right)\frac{lb}{ft}\\ W_d=396.6\frac{lb}{ft}\end{array}$

Now, calculate the live load on the beam as follows

$W_L=\left(w_{sl}\right)L_p$

Where the construction load on the slab is $w_{sl}$

$\begin{array}{l}{W}_L=20psf\times 6.5ft\\ W_L=130\frac{lb}{ft}\end{array}$

The uniformly distributed factored load can be found as

$W_u=1.2W_d+1.6W_l$

Where, $W_d$ is the uniformly distributed dead load on the beam and applied live load on the beam is $W_l$

Substitute the values in the above equation, we have

$\begin{array}{l}{W}_u=\left[0.3966\right]+\left[0.130\right]\\ W_u=0.5266\frac{Kips}{ft}\end{array}$

Calculate the maximum bending moment on the beam;

$M_{ul}=\frac{w_u{L}_{AB}^2}{8}$

Where, $M_{ul}$ is the maximum bending moment and $L_{AB}^{}$ is the length of the beam.

$\begin{array}{l}{M}_{ul}=\frac{w_u{L}_{AB}^2}{8}\\ M_{ul}=\frac{\left(0.5622\times {36}^2\right)}{8}\frac{Kips}{ft}f{t}^2\\ M_{ul}=85.3Kips\text{-}ft.\end{array}$

Check the value of the nominal flexural strength of W- sections from the Manual:

Flexural strength of the beam before curing is given as follows:

$\begin{array}{l}\frac{M_n}{{\Omega }_b}=\frac{M_P}{{\Omega }_b}\\ =135Kips.ft\end{array}$

Where, $\frac{M_n}{{\Omega }_b}$ is the allowable flexural strength

Comparing the values of $\frac{M_n}{{\Omega }_b}$ and $M_a$, We have

$\begin{array}{l}85.3Kips\text{-}ft<135Kips.ft\\ M_a<\frac{M_n}{{\Omega }_b}\end{array}$

Thus, the beam is satisfactory before the curing of concrete is complete.

Conclusion:

Therefore, $\text{W}16X31$ is satisfactory to use.

To determine

(c)

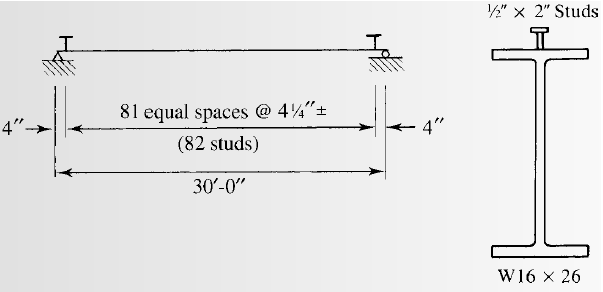
Selecting the stud anchors for the given section.

Answer to Problem 9.5.1P

we will use $96$ Studs with $\frac{1}{2}inch\times 2inch$ dimension spaced at $4.5inch$.

Explanation of Solution

Calculation:

We have to check whether the studs satisfy the ASIC specifications.

From AISC specifications the maximum stud diameter will be equal to

$d_{\text{maximum}}=2.5t_f$

Where, $d_{\text{maximum}}$ is the maximum diameter and $t_f$ is the flange thickness.

Substitute the values in the equation, we get

$\begin{array}{l}{d}_{\text{maximum}}=2.5\times 0.440\\ d_{\text{maximum}}=1.1\text{in}\text{.}\end{array}$

Try for, $\frac{1}{2}in\times 2in$ stud is a satisfactory stud element.

The area of stud using the following equation as follows:

$A{}_{stud}=\frac{\pi }{4}{d}^2$

Where, the diameter of the stud is d.

Substitute $\frac{1}{2}in$ for d

$\begin{array}{l}A{}_{stud}=\frac{\pi }{4}{\left[\frac{1}{2}\right]}^{2}i{n}^2\\ A{}_{stud}=0.1963i{n}^2\end{array}$

We have the modulus of elasticity of concrete as follows:

$E_C={\left(w_C\right)}^{\frac{3}{2}}\sqrt{f_C^{\text{'}}}ksi$

Where, the modulus of elasticity of concrete is $E_C$,

unit weight of concrete is $w_C$ and

the 28-day compressive strength of concrete is $f_C^{\text{'}}$.

Substitute $145\frac{lb}{f{t}^3}$ for $w_C$ and $4ksi$ for $f_C^{\text{'}}$.

$\begin{array}{l}{E}_C={\left(145\frac{lb}{f{t}^3}\right)}^{\frac{3}{2}}\sqrt{4}ksi\\ E_C=1746.03\frac{lb}{f{t}^3}\times 2ksi\\ E_C=3492.06ksi.\end{array}$

Calculating the shear strength of stud with the following formula:

$Q_n=0.5A_{stud}\sqrt{f_C^{\text{'}}{E}_C}$

Substitute the values, we get

$\begin{array}{l}{Q}_n=0.5\times 0.1963\sqrt{4ksi\times 3492ksi}\\ Q_n=11.60kips\end{array}$

Now, the upper limit of the shear strength is as follows:

$\begin{array}{l}{Q}_{nn}=R_g{R}_p{A}_{stud}{F}_u\\ Q_{nn}=1.00\times 0.75\times 0.1963i{n}^2\times 65ksi\\ Q_{nn}=9.570kips.\end{array}$

As, the calculated value is less than the upper limit given by AISC, take the shear strength as:

$Q_n=9.570kips.$

The number of studs required for the half beam are as follows:

$N\text{'}=\frac{V}{Q_n}$

Substitute the values, we have

$\begin{array}{l}N\text{'}=\frac{456.5Kips}{9.57Kips}\\ N\text{'}=47.7\\ N\text{'}=48\end{array}$

The number of studs required are as follows:

$N=2N\text{'}$

Substitute the values, we have

$\begin{array}{l}N=2\times 48\\ N=96\end{array}$

Calculate the spacing of the studs as following:

The minimum longitudinal spacing for the studs will be as follows:

$S_{\text{t,}\text{minimum}}=6d$

Where, the minimum longitudinal spacing for the studs is $S_{\text{t,}\text{minimum}}$ and d is the diameter of the stud.

$S_{\text{t,}\text{minimum}}=6d$

Substitute the values, we have

$\begin{array}{l}{S}_{\text{t,}\text{minimum}}=6d\\ S_{\text{t,}\text{minimum}}=6\times 0.5inch\\ S_{\text{t,}\text{minimum}}=3inch.\end{array}$

The minimum transversal spacing for the studs will be as follows:

$S_{\text{t,}\text{minimum}}=4d$

Where, the minimum transversal spacing for the studs is $S_{\text{t,}\text{minimum}}$ and d is the diameter of the stud.

$S_{\text{t,}\text{minimum}}=4d$

Substitute the values, we have

$\begin{array}{l}{S}_{\text{t,}\text{minimum}}=4d\\ S_{\text{t,}\text{minimum}}=4\times 0.5inch\\ S_{\text{t,}\text{minimum}}=2inch.\end{array}$

The maximum longitudinal spacing for the studs will be as follows:

$S_{\text{t,}\text{maximum}}=8t$

Where, the maximum longitudinal spacing for the studs is $S_{\text{t,}\text{maximum}}$ and t is the thickness of the concrete slab.

$S_{\text{t,}\text{maximum}}=8t$

Substitute the values, we have

$\begin{array}{l}{S}_{\text{t,}\text{maximum}}=8t\\ S_{\text{t,}\text{maximum}}=8\times 4.5inch\\ S_{\text{t,}\text{maximum}}=36inch.\end{array}$

Therefore, the upper limit of the spacing is 36 inches.

Calculating the spacing for a stud at each section by the following formula:

$S=\frac{L}{N}$

Where, S is the spacing required

$\begin{array}{l}S=\frac{L}{N}\\ S=\frac{36\times 12}{96}\\ S=4.5inch\end{array}$

Conclusion:

Therefore, we will use $96$ Studs with $\frac{1}{2}inch\times 2inch$ dimension spaced at $4.5inch$.