
Concept explainers
(a)
The moment of inertia of the transformed section.
Answer to Problem 9.1.1P
Explanation of Solution
Given:
A W 18 X 40 floor beam, the 28-day compressive strength of the concrete is
Calculation:
We have the modulus of elasticity of concrete as follows:
Where, the modulus of elasticity of concrete is
unit weight of concrete is
the 28-day compressive strength of concrete is
Substitute
Modular ratio by using the following formula:
Where, the modulus of elasticity of concrete is
the modulus of elasticity of steel is
and n is the modular ratio.
Substitute
Now the section will be transformed.
Since the modulus of elasticity of concrete can only be approximated, the usual practice of rounding n to the nearest whole number is sufficiently accurate. Thus,
The transformed width of the section is as following:
Where,
Substitute
Following is the section for the given set of conditions:
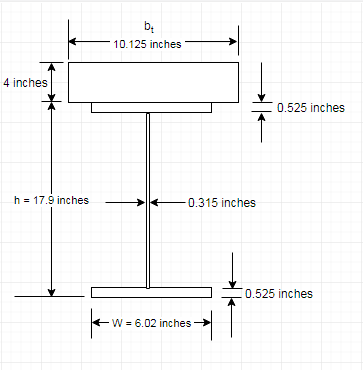
Data from the steel code:
| DesignationImperial (in x lb/ft) | Depthh (in) | Widthw (in) | Web Thicknesstw (in) | Flange Thicknesstf (in) | Sectional Area (in2) | Weight (lbf/ft) | Static Parameters | |||
| Moment of Inertia | Elastic Section Modulus | |||||||||
| Ix (in4) | Iy (in4) | Sx (in3) | Sy (in3) | |||||||
| W 18 x 40 | 17.9 | 6.02 | 0.315 | 0.525 | 11.8 | 40 | 612 | 19.1 | 68.4 | 6.4 |
The transformed section is shown in the above figure. The neutral axis is not known yet whether it lies in the steel or the concrete.
The location of the neutral axis can be found by applying the principle of moments with the axis of moments at the top of the slab. The computations are summarized in Table, and the distance from the top of the slab to the centroid is:
| Component | |||
| Concrete | |||
| W 18 X 40 | |||
| Sum |
The distance of centroid of the section is as follows:
Substitute
Since this is greater than 4 inches (the thickness of the slab) the neutral axis lies below the slab in the web. Applying the parallel axis theorem and tabulating the computations in table, we obtain the moment of inertia of the transformed section as:
| Component | |||||
| Concrete | |||||
| W 18 X 40 | |||||
| Sum |
Conclusion:
Therefore, total moment of inertia of the transformed section is
(b)
The stress at the top of the steel (indicate whether tension or compression), the stress at the bottom of the steel, and the stress at the top of the concrete.
Answer to Problem 9.1.1P
Explanation of Solution
Given:
Positive service load moment of 290 ft-kips.
Calculation:
For the computation of the stress at top of the steel is as following:
Where, the stress at the top of the steel is
The distance from neutral axis to top of steel section is as follows:
Here the thickness of the concrete slab is t.
Compute the stress at top of the steel as:
As, the centroid lies below the top of the steel, the stress is compressive.
Now, the stress at the bottom of the steel is as follows:
The distance from the neutral axis to bottom of steel section.
Where,
As, the centroid lies above the top of steel, the stress is tensile.
Stress at the top of the slab is as follows:
Where, n is the modular ratio is n.
As the concrete slab is above the neutral axis, hence the stress is compressive.
Conclusion:
Therefore, the stress at top of steel section is
Want to see more full solutions like this?
Chapter 9 Solutions
Steel Design (Activate Learning with these NEW titles from Engineering!)
- Determine the stiffness matirx of the entire truss in Global co-ordinate system, clearly indicate the degrees of freedom numbers in the stiffness matrix.arrow_forwardDetermine the stiffness matrices of elements 2, 3 and 4 in the global co-ordinate system. Assume A=0.0015m2 and E=200GPa, indicate the degrees of freedom in all stiffness matricies.arrow_forwardA short plain concrete column with cross-section dimensions of 12 in x 12 in is to be constructed. If the compressive strength of the concrete (f’c) is 5000 psi, what is the maximum load that can be safely applied to the column? - 600 k - 950 k - 720 k - 347 karrow_forward
- The borrow pit has 2000 cyds of suitable fill. The fill required for the project is 1900 cyds. The swell factor is 10% and the shrinkage factor is 15%. How much more borrow do we need? Or is there extra? - 13 yards extra - 13 yards short - 200 yards extra - 161 yards shortarrow_forwardThe job site has a primary vertical control point with a reference benchmark of 100 ft. An instrument is set up with an HI of 5.42 ft above the BM. A grade stake is set at an elevation of 96 ft. What is the height reading on the rod at the grade stake? - 9.42 ft - 4.00 ft - 1.42 ft - 5.42 ftarrow_forwardAssume you have a simple beam 16 ft long supported on each end by R1 and R2. There is a concentrated load of 900 lb that is 4 ft from R2. Reaction R1 is pinned 12 ft from the load. Reaction R1 is 225 lb and R2 is 675 lb. What is the maximum bending moment in pounds per foot? - 3,600 - 1,800 - 2,700- 900arrow_forward
- A wall form is four-feet high, ten-feet long and ten-feet wide. It is full of fluid concrete. What is the pressure at the bottom of the form? - 86,400 psi - 60,000 psf - 600 psf - 60,000 psiarrow_forwardhe sides of a building are 300 feet long and 200 feet wide. What is the diagonal distance between the opposite corners? - 300 feet - 306 feet - 360.60 feet - 306.6 feetarrow_forwardThe excavation for a square basement requires a 1:2 H:V slope cut back. The external dimensions of the footings are 30 x 30 feet. The excavation is 8 feet deep and you need to add 2 feet on each side to install the footing forms. What is the volume of cubic yards of excavation? - 486.7cy - 13140cy - 858.8cy - 429.4cyarrow_forward
- The Modulus of Elasticity is 30,000,000 for mild carbon steel. In the plastic state, the unit stress is 25000 psi. What is the strain? - 1.45 - 145.0 - 0.00083 - 1450.0arrow_forwardThe building is twenty-five feet by twenty five feet. The side line of the building and two corners along the line have been staked. What is the diagonal distance and the 90 degree distance to the other corners? - 35.36 feet and 35.36 feet - 25.00 feet and 35.36 feet - 35.36 feet and 25 feet - 25.00 feet and 25.00 feetarrow_forwardNEED HELP THANK YOU IN ADVACEarrow_forward
 Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning
Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning
Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning Architectural Drafting and Design (MindTap Course...Civil EngineeringISBN:9781285165738Author:Alan Jefferis, David A. Madsen, David P. MadsenPublisher:Cengage Learning
Architectural Drafting and Design (MindTap Course...Civil EngineeringISBN:9781285165738Author:Alan Jefferis, David A. Madsen, David P. MadsenPublisher:Cengage Learning Fundamentals Of Construction EstimatingCivil EngineeringISBN:9781337399395Author:Pratt, David J.Publisher:Cengage,
Fundamentals Of Construction EstimatingCivil EngineeringISBN:9781337399395Author:Pratt, David J.Publisher:Cengage, Construction Materials, Methods and Techniques (M...Civil EngineeringISBN:9781305086272Author:William P. Spence, Eva KultermannPublisher:Cengage Learning
Construction Materials, Methods and Techniques (M...Civil EngineeringISBN:9781305086272Author:William P. Spence, Eva KultermannPublisher:Cengage Learning





