FLUID MECHANICS FUND. (LL)-W/ACCESS
4th Edition
ISBN: 9781266016042
Author: CENGEL
Publisher: MCG CUSTOM
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 9, Problem 88P
Consider steady, incompressible, parallel, laminar flow falling between two infinite vertical walls (Fig. 9-88). The distance between the walls is h, and gravity acts in the negative z-direction (downward in the figure). There is no applied (forced) pressure driving the flow-the fluid falls by gravity alone. The pressure is constant everywhere in the flow field. Calculate the velocity field and sketch the velocity profile using appropriate nondimensionalized variable.
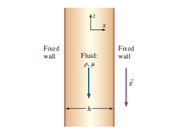
FIGURE P9-88
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
V
u-v
Question 4: Consider fully developed Couette flow - flow between
two infinite parallel plates separated by distance h, with the top
plate moving and the bottom plate stationary as illustrated. The flow
is steady, incompressible, and two dimensional in the xy-plane. The
velocity field is given by V = (u,v) = (V y/h)ỉ + 0ỷ, Generate an
expression for stream function Yalong the vertical dashed line in
the figure. For convenience, 4= 0 along the bottom wall of the channel. What is the value of Y
along the top wall?
Consider steady, incompressible, parallel, laminar flow of a viscous fluid falling between two infinite vertical walls. The distance between the walls is h, and gravity acts in the negative z-direction (downward in the figure). There is no applied (forced) pressure driving the flow—the fluid falls by gravity alone. The pressure is constant everywhere in the flow field. Calculate the velocity field and sketch the velocity profile using appropriate nondimensionalized variables.
Question 1: Consider fully developed two-dimensional Poiseuille flow: flow between two infinite
parallel plates separated by distance h, with both the top plate and bottom plate stationary, and a
forced pressure gradient dP/dx driving the flow as
illustrated in the figure (dP/dx is constant and
negative). The flow is steady, incompressible, and
two-dimensional in the xy-plane. The velocity
components are given by
1 dP
u = -(y² - hy); v = 0
2μ αχ
h
where μ is the fluid's viscosity. Is this flow rotational or irrotational?
u(y)
a. If it is rotational, calculate the vorticity component in the z-direction. Do fluid particles in this
flow rotate clockwise or counterclockwise?
b. calculate the linear strain rates in the x- and y-directions, and
c. calculate the shear strain rate Exy.
d. Combine your results to form the two-dimensional strain rate tensor εij in the xy-plane,
Chapter 9 Solutions
FLUID MECHANICS FUND. (LL)-W/ACCESS
Ch. 9 - Explain the fundamental differences between a flow...Ch. 9 - What does it mean when we say that two more...Ch. 9 - The divergence theorem is v.cdv=A c . n dACh. 9 - Prob. 4CPCh. 9 - Prob. 5CPCh. 9 - Prob. 6CPCh. 9 - Prob. 7PCh. 9 - Prob. 8PCh. 9 - Let vector G=2xzi12x2jz2kk . Calculate the...Ch. 9 - Prob. 10P
Ch. 9 - Prob. 11PCh. 9 - Prob. 12PCh. 9 - Prob. 13PCh. 9 - Alex is measuring the time-averaged velocity...Ch. 9 - Let vector c be given G=4xziy2i+yzkand let V be...Ch. 9 - The product rule can be applied to the divergence...Ch. 9 - Prob. 18PCh. 9 - Prob. 19PCh. 9 - Prob. 20CPCh. 9 - In this chapter we derive the continuity equation...Ch. 9 - Repeat Example 9-1(gas compressed in a cylinder by...Ch. 9 - Consider the steady, two-dimensional velocity...Ch. 9 - The compressible from of the continuity equation...Ch. 9 - In Example 9-6 we derive the equation for...Ch. 9 - Consider a spiraling line vortex/sink flow in the...Ch. 9 - Verify that the steady; two-dimensional,...Ch. 9 - Consider steady flow of water through an...Ch. 9 - Consider the following steady, three-dimensional...Ch. 9 - Consider the following steady, three-dimensional...Ch. 9 - Two velocity components of a steady,...Ch. 9 - Imagine a steady, two-dimensional, incompressible...Ch. 9 - The u velocity component of a steady,...Ch. 9 - Imagine a steady, two-dimensional, incompressible...Ch. 9 - The u velocity component of a steady,...Ch. 9 - What is significant about curves of constant...Ch. 9 - In CFD lingo, the stream function is often called...Ch. 9 - Prob. 39CPCh. 9 - Prob. 40CPCh. 9 - Prob. 41PCh. 9 - Prob. 42PCh. 9 - Prob. 44PCh. 9 - Prob. 45PCh. 9 - As a follow-up to Prob. 9-45, calculate the volume...Ch. 9 - Consider the Couette flow of Fig.9-45. For the...Ch. 9 - Prob. 48PCh. 9 - AS a follow-up to Prob. 9-48, calculate the volume...Ch. 9 - Consider the channel flow of Fig. 9-45. The fluid...Ch. 9 - In the field of air pollution control, one often...Ch. 9 - Suppose the suction applied to the sampling...Ch. 9 - Prob. 53PCh. 9 - Flow separates at a shap corner along a wall and...Ch. 9 - Prob. 55PCh. 9 - Prob. 56PCh. 9 - Prob. 58PCh. 9 - Prob. 59PCh. 9 - Prob. 60PCh. 9 - Prob. 61PCh. 9 - Prob. 62PCh. 9 - Prob. 63EPCh. 9 - Prob. 64PCh. 9 - Prob. 65EPCh. 9 - Prob. 66PCh. 9 - Prob. 68EPCh. 9 - Prob. 69PCh. 9 - Prob. 71PCh. 9 - Prob. 72PCh. 9 - Prob. 73PCh. 9 - Prob. 74PCh. 9 - Prob. 75PCh. 9 - Wht in the main distionction between Newtormine...Ch. 9 - Prob. 77CPCh. 9 - What are constitutive equations, and to the fluid...Ch. 9 - An airplane flies at constant velocity Vairplane...Ch. 9 - Define or describe each type of fluid: (a)...Ch. 9 - The general cool volume from of linearmomentum...Ch. 9 - Consider the steady, two-dimensional,...Ch. 9 - Consider the following steady, two-dimensional,...Ch. 9 - Consider the following steady, two-dimensional,...Ch. 9 - Consider liquid in a cylindrical tank. Both the...Ch. 9 - Engine oil at T=60C is forced to flow between two...Ch. 9 - Consider steady, two-dimensional, incompressible...Ch. 9 - Consider steady, incompressible, parallel, laminar...Ch. 9 - Prob. 89PCh. 9 - Prob. 90PCh. 9 - Prob. 91PCh. 9 - The first viscous terms in -comonent of the...Ch. 9 - An incompressible Newtonian liquid is confined...Ch. 9 - Prob. 94PCh. 9 - Prob. 95PCh. 9 - Prob. 96PCh. 9 - Prob. 97PCh. 9 - Consider steady, incompressible, laminar flow of a...Ch. 9 - Consider again the pipe annulus sketched in Fig...Ch. 9 - Repeat Prob. 9-99 except swap the stationary and...Ch. 9 - Consider a modified form of Couette flow in which...Ch. 9 - Consider dimensionless velocity distribution in...Ch. 9 - Consider steady, incompressible, laminar flow of a...Ch. 9 - Prob. 104PCh. 9 - Prob. 105PCh. 9 - Prob. 106PCh. 9 - Prob. 107CPCh. 9 - Prob. 108CPCh. 9 - Discuss the relationship between volumetric strain...Ch. 9 - Prob. 110CPCh. 9 - Prob. 111CPCh. 9 - Prob. 112PCh. 9 - Prob. 113PCh. 9 - Look up the definition of Poisson’s equation in...Ch. 9 - Prob. 115PCh. 9 - Prob. 116PCh. 9 - Prob. 117PCh. 9 - For each of the listed equation, write down the...Ch. 9 - Prob. 119PCh. 9 - Prob. 120PCh. 9 - A block slides down along, straight inclined wall...Ch. 9 - Water flows down a long, straight, inclined pipe...Ch. 9 - Prob. 124PCh. 9 - Prob. 125PCh. 9 - Prob. 126PCh. 9 - Prob. 128PCh. 9 - The Navier-Stokes equation is also known as (a)...Ch. 9 - Which choice is not correct regarding the...Ch. 9 - In thud flow analyses, which boundary condition...Ch. 9 - Which choice is the genera1 differential equation...Ch. 9 - Which choice is the differential , incompressible,...Ch. 9 - A steady, two-dimensional, incompressible flow...Ch. 9 - A steady, two-dimensional, incompressible flow...Ch. 9 - A steady velocity field is given by...Ch. 9 - Prob. 137P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Question 1: Consider fully developed two-dimensional Poiseuille flow: flow between two infinite parallel plates separated by distance h, with both the top plate and bottom plate stationary, and a forced pressure gradient dP/dx driving the flow as illustrated in the figure (dP/dx is constant and negative). The flow is steady, incompressible, and two-dimensional in the xy-plane. The velocity components are given by 1 dP u(y) u = 2μ dx (y²hy); v = 0 where is the fluid's viscosity. Is this flow rotational or irrotational? a. If it is rotational, calculate the vorticity component in the z-direction. Do fluid particles in this flow rotate clockwise or counterclockwise? b. calculate the linear strain rates in the x- and y-directions, and c. calculate the shear strain rate ɛxy. d. Combine your results to form the two-dimensional strain rate tensor εij in the xy-plane,arrow_forwardConsider steady, incompressible, two-dimensional flow through a converging duct (Figure below). Uo A simple approximate velocity field for this flow of the Converging duct flow is modeled by the steady, two- dimensional velocity field given by: V = (u, v) = (U, + bx)i – byj The pressure field is given by: P = P, – 2U,bx + b*(x² + y²) Where Po is the pressure at x = 0. Generate an expression for the rate of change of pressure following a fluid particle?arrow_forwardAnswer the following question using the format given.arrow_forward
- Consider fully developed Couette flow between two infinite parallel plates separated by distance h, with the top plate moving and the bottom plate stationary, as illustrated in the figure below. The flow is steady, incompressible, and two-dimensional in the XY plane. The velocity field is given by V }i = (u, v) = (v² )i +0j = V (a) Find out the acceleration field of this flow. (b) Is this flow steady? What are the u and v components of velocity? u= V² harrow_forwardpls answer question with steparrow_forwardConsider steady, incompressible, parallel, laminar flow of a film of oil falling slowly down an infinite vertical wall. The oil film thickness is h, and gravity acts in the negative z-direction. There is no applied (forced) pressure driving the flow—the oil falls by gravity alone., except for the case in which the wall is inclined at angle ?. Generate expressions for both the pressure and velocity fields. As a check, make sure that your result agrees with that of when ? = 90°. [Hint: It is most convenient to use the (s, y, n) coordinate system with velocity components (us, ?, un), where y is into the page in Fig. Plot the dimensionless velocity profile us* versus n* for the case in which ? = 60°.]arrow_forward
- Consider steady, incompressible, laminar, fully developed, planar Poiseuille flow between two parallel, horizontal plates (velocity and pressure profiles are shown in Fig. At some horizontal location x = x1, the pressure varies linearly with vertical distance z, as sketched. Choose an appropriate datum plane (z = 0), sketch the profile of modi fied pressure all along the vertical slice, and shade in the region representing the hydrostatic pressure component. Discuss.arrow_forwardI want to answer all the questions by handwriting.arrow_forwardConsider fully developed Couette flow-flow between two infinite parallel plates separated by distance h, with the top plate moving and the bottom plate stationary as illustrated in figure below. The flow is steady, incompressible, and two-dimensional in the xy-plane. The velocity field is given by: V = (u, v) = V +07 h Is this flow rotational or irrotational? If it is rotational, calculate the vorticity component in the z- direction. Do fluid particles in this flow rotate clockwise or counterclockwise? u = varrow_forward
- A velocity field of the two-dimensional, time-dependent fluid flow is given by where t is time. Find the material derivative Du/Dt and hence calculate the acceleration of the fluid at any time t > 0 and any pont x > 0, y > 0. a) Incompressibility a) Is this flow incompressible (i.e. it has zero divergence)? Yes No ди Ət b) Time derivative of flow field Calculate the time derivative of the velocity. Represent your answer in the form i+ || 3 3 u(t, x, y) =r? (x² + y² ) i− {etxtyj X уј 3 a = c) Material derivative and acceleration Calculate the material derivative of the velocity and hence the acceleration a. Represent your answer in the form Du Dt || j i+ jarrow_forwardi didnt understand 3 fluid mechanics questions. please help me :) i will send of the three partarrow_forwardg Figure 3: Fluid flows between two infinite plates A viscous, incompressible steady fluid flows between two infinite, vertical, parallel plates distance h apart, as shown in Figure 3. Use the given coordinates system and assume that the flow is laminar, fully developed (30), and planar (w = 0,0). Assume that pressure and gravity are not negligible. (a) Simplify the contnuity equation and show that v = 0. (b) Using the y-momentum equation show that pressure is a function of a only. (c) Find the velocity distribution u(y) in terms of u, g, h, p and d (d) Find the wall shear stress of the flow.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Introduction to Kinematics; Author: LearnChemE;https://www.youtube.com/watch?v=bV0XPz-mg2s;License: Standard youtube license