
(a)
To Identify: The before and after situations, and to draw a diagram of both.
(a)
Explanation of Solution
Given:
Mass of the fullback is
Initial velocity of the fullback is
Mass of the defensive tackle is
Defensive tackle moving in the direction opposite to that of fullback.
Final speed of both players is zero. That is
Before collision:
After collision:
The diagrams showing the situation before and after the collision between the players are as shown in figure
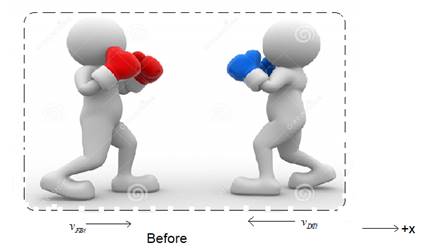
Figure 1
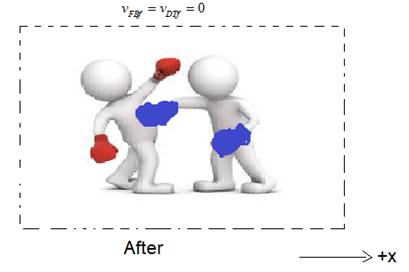
Figure 2
(b)
The fullback’s momentum before collision.
(b)
Answer to Problem 69A
Explanation of Solution
Given:
Mass of the fullback is
Initial velocity of the fullback is
Formula used:
Momentum
Initial momentum of fullback can be calculated using the equation,
Where,
Calculation:
Substituting the numerical values in equation
Conclusion:
The fullback’s momentum before collision is
(c)
The change in fullback’s momentum.
(c)
Answer to Problem 69A
Explanation of Solution
Given:
Mass of the fullback is
Initial velocity of the fullback is
Final velocity of the fullback is
Formula used:
Change in momentum = final momentum − initial momentum
That is,
Momentum
Hence the initial momentum of the fullback can be written as,
Where,
And, the final momentum of the fullback can be written as,
Where
Therefore, change in momentum of the fullback is,
Substituting for
Calculation:
Substituting the numerical values in equation
Conclusion:
The change in fullback’s momentum is
(d)
The change in defensive tackle’s momentum.
(d)
Answer to Problem 69A
Explanation of Solution
Since defensive tackle running in the direction opposite to the direction of motion of fullback, the change in defensive tackle’s momentum is
(e)
The defensive tackle’s original momentum.
(e)
Answer to Problem 69A
Explanation of Solution
Since the defensive tackle running in the direction opposite to the direction of motion of fullback, the initial momentum of defensive tackle is
(f)
The Defensive tackles initial velocity.
(f)
Answer to Problem 69A
Explanation of Solution
Given:
Mass of the defensive tackle is
Formula used:
Momentum
Hence the initial momentum of the defensive tackle can be written as,
Where,
Calculation:
From the part (e), the initial momentum of defensive tackle is
Initial velocity of the defensive tackle can be calculated by substituting the numerical values in equation
Conclusion:
The Defensive tackle’s initial velocity is
Chapter 9 Solutions
Glencoe Physics: Principles and Problems, Student Edition
Additional Science Textbook Solutions
Biology: Life on Earth (11th Edition)
Microbiology with Diseases by Body System (5th Edition)
College Physics: A Strategic Approach (3rd Edition)
Biological Science (6th Edition)
Genetic Analysis: An Integrated Approach (3rd Edition)
Chemistry: Structure and Properties (2nd Edition)
- (a) For a spherical capacitor with inner radius a and outer radius b, we have the following for the capacitance. ab C = k₂(b- a) 0.0695 m 0.145 m (8.99 × 10º N · m²/c²)( [0.145 m- 0.0695 m × 10-11 F = PF IIarrow_forwardA pendulum bob A (0.5 kg) is given an initialspeed of vA = 4 m/s when the chord ishorizontal. It then hits a stationary block B (1kg) which then slides to a maximum distanced before it stops. Determine the value of d.The coefficient of static friction between theblock and the plane is μk = 0.2. The coefficientof restitution between A and B is e = 0.8.Ans: d=1.0034 marrow_forwardFigure 29-43 Problem 12. ••13 In Fig. 29-44, point P₁ is at distance R = 13.1 cm on the perpendicular bisector of a straight wire of length L = 18.0 cm carrying current i = 58.2 mA. (Note that the wire is not long.) What is the magnitude of the magnetic field at P₁ due to i? P2° R R Larrow_forward
- Checkpoint 1 The figure shows the current i in a single-loop circuit with a battery B and a resistance R (and wires of neg- ligible resistance). (a) Should the emf arrow at B be drawn pointing leftward or rightward? At points a, B C R b, and c, rank (b) the magnitude of the current, (c) the electric potential, and (d) the electric potential energy of the charge carriers, greatest first.arrow_forwardPls help ASAParrow_forwardPls help asaparrow_forward
- Pls help asaparrow_forward3. If the force of gravity stopped acting on the planets in our solar system, what would happen? a) They would spiral slowly towards the sun. b) They would continue in straight lines tangent to their orbits. c) They would continue to orbit the sun. d) They would fly straight away from the sun. e) They would spiral slowly away from the sun. 4. 1 The free-body diagram of a wagon being pulled along a horizontal surface is best represented by A F N B C 0 Ꭰ FN E a) A b) B c) C app app The app 10 app d) e) ס ח D E 10 apparrow_forwardPls help ASAParrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





