Physics For Scientists And Engineers With Modern Physics, 9th Edition, The Ohio State University
9th Edition
ISBN: 9781305372337
Author: Raymond A. Serway | John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 9, Problem 68AP
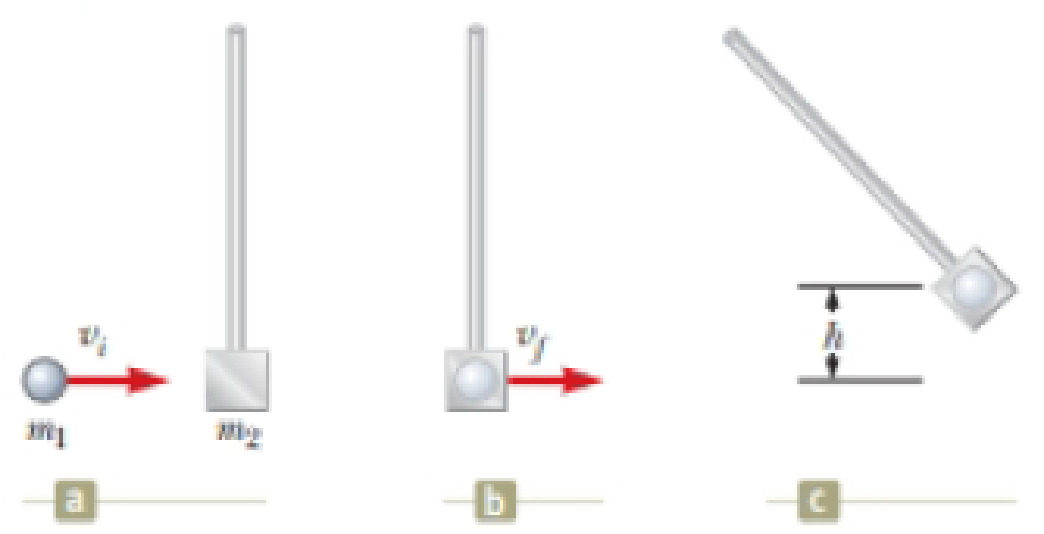
(a) Figure P9.36 shows three points in the operation of the ballistic pendulum discussed in Example 9.6 (and shown in Fig. 9.10b). The projectile approaches the pendulum in Figure P9.36a. Figure P9.36b shows the situation just after the projectile is captured in the pendulum. In Figure P9.36c, the pendulum arm has swung upward and come to rest momentarily at a height A above its initial position. Prove that the ratio of the kinetic energy of the projectile–pendulum system immediately after the collision to the kinetic energy immediately before is m1|/(m1 + m2). (b) What is the ratio of the momentum of the system immediately after the collision to the momentum immediately before? (c) A student believes that such a large decrease in mechanical energy must be accompanied by at least a small decrease in momentum. How would you convince this student of the truth?
Figure P9.36 Problem. 36 and 43. (a) A metal ball moves toward the pendulum. (b) The ball is captured by the pendulum. (c) The ball–pendulum combination swings up through a height h before coming to rest.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
I do not understand the process to answer the second part of question b. Please help me understand how to get there!
Rank the six combinations of electric charges on the basis of the electric force acting on 91. Define forces pointing to the right as positive and forces pointing to the left as negative.
Rank in increasing order by placing the most negative on the left and the most positive on the right. To rank items as equivalent, overlap them.
▸ View Available Hint(s)
[most negative
91 = +1nC
92 = +1nC
91 = -1nC
93 = +1nC
92- +1nC
93 = +1nC
-1nC
92- -1nC
93- -1nC
91= +1nC
92 = +1nC
93=-1nC
91
+1nC
92=-1nC
93=-1nC
91 = +1nC
2 = −1nC
93 = +1nC
The correct ranking cannot be determined.
Reset
Help
most positive
Part A
Find the x-component of the electric field at the origin, point O.
Express your answer in newtons per coulomb to three significant figures, keeping in mind that an x component that points to the right is positive.
▸ View Available Hint(s)
Eoz =
Η ΑΣΦ
?
N/C
Submit
Part B
Now, assume that charge q2 is negative; q2 = -6 nC, as shown in (Figure 2). What is the x-component of the net electric field at the origin, point O?
Express your answer in newtons per coulomb to three significant figures, keeping in mind that an x component that points to the right is positive.
▸ View Available Hint(s)
Eoz=
Η ΑΣΦ
?
N/C
Chapter 9 Solutions
Physics For Scientists And Engineers With Modern Physics, 9th Edition, The Ohio State University
Ch. 9.1 - Two objects have equal kinetic energies. How do...Ch. 9.1 - Your physical education teacher throws a baseball...Ch. 9.3 - Two objects are at rest on a frictionless surface....Ch. 9.3 - Rank an automobile dashboard, seat belt, and air...Ch. 9.4 - Prob. 9.5QQCh. 9.4 - A table-tennis ball is thrown at a stationary...Ch. 9.6 - A baseball bat of uniform density is cut at the...Ch. 9.7 - A cruise ship is moving at constant speed through...Ch. 9 - Prob. 1OQCh. 9 - Prob. 2OQ
Ch. 9 - Prob. 3OQCh. 9 - Prob. 4OQCh. 9 - Prob. 5OQCh. 9 - Prob. 6OQCh. 9 - The momentum of an object is increased by a factor...Ch. 9 - The kinetic energy of an object is increased by a...Ch. 9 - If two particles have equal momenta, are their...Ch. 9 - Prob. 10OQCh. 9 - Prob. 11OQCh. 9 - Two particles of different mass start from rest....Ch. 9 - Prob. 13OQCh. 9 - A basketball is tossed up into the air, falls...Ch. 9 - Prob. 15OQCh. 9 - Prob. 16OQCh. 9 - Prob. 17OQCh. 9 - Prob. 18OQCh. 9 - Prob. 1CQCh. 9 - Prob. 2CQCh. 9 - Prob. 3CQCh. 9 - While in motion, a pitched baseball carries...Ch. 9 - You are standing perfectly still and then take a...Ch. 9 - Prob. 6CQCh. 9 - Two students hold a large bed sheet vertically...Ch. 9 - A juggler juggles three balls in a continuous...Ch. 9 - Prob. 9CQCh. 9 - Does a larger net force exerted on an object...Ch. 9 - Does a larger net force always produce a larger...Ch. 9 - A bomb, initially at rest, explodes into several...Ch. 9 - A particle of mass m moves with momentum of...Ch. 9 - Prob. 2PCh. 9 - Prob. 3PCh. 9 - A 3.00-kg particle has a velocity of...Ch. 9 - A baseball approaches home plate at a speed of...Ch. 9 - Prob. 6PCh. 9 - Prob. 7PCh. 9 - A 65.0-kg boy and his 40.0-kg sister, both wearing...Ch. 9 - Prob. 9PCh. 9 - When you jump straight up as high as you can, what...Ch. 9 - Two blocks of masses m and 3m are placed on a...Ch. 9 - Prob. 12PCh. 9 - An estimated forcetime curve for a baseball struck...Ch. 9 - Prob. 14PCh. 9 - A glider of mass m is free to slide along a...Ch. 9 - Prob. 16PCh. 9 - The front 1.20 m of a 1 400-kg car Ls designed as...Ch. 9 - A tennis player receives a shot with the ball...Ch. 9 - The magnitude of the net force exerted in the x...Ch. 9 - Prob. 20PCh. 9 - Water falls without splashing at a rate of 0.250...Ch. 9 - A 1 200-kg car traveling initially at vCi = 25.0...Ch. 9 - Prob. 23PCh. 9 - A car of mass m moving at a speed v1 collides and...Ch. 9 - A railroad car of mass 2.50 104 kg is moving with...Ch. 9 - Prob. 26PCh. 9 - Prob. 27PCh. 9 - A 7.00-g bullet, when fired from a gun into a...Ch. 9 - A tennis ball of mass 57.0 g is held just above a...Ch. 9 - Prob. 30PCh. 9 - Prob. 31PCh. 9 - Prob. 32PCh. 9 - Prob. 33PCh. 9 - (a) Three carts of masses m1 = 4.00 kg, m2 = 10.0...Ch. 9 - Prob. 35PCh. 9 - Prob. 36PCh. 9 - Prob. 37PCh. 9 - Two shuffleboard disks of equal mass, one orange...Ch. 9 - Prob. 39PCh. 9 - A proton, moving with a velocity of vii, collides...Ch. 9 - Prob. 41PCh. 9 - A 90.0-kg fullback running east with a speed of...Ch. 9 - Prob. 43PCh. 9 - Prob. 44PCh. 9 - Prob. 45PCh. 9 - Prob. 46PCh. 9 - Explorers in the jungle find an ancient monument...Ch. 9 - A uniform piece of sheet metal is shaped as shown...Ch. 9 - A rod of length 30.0 cm has linear density (mass...Ch. 9 - Prob. 50PCh. 9 - Prob. 51PCh. 9 - Consider a system of two particles in the xy...Ch. 9 - Prob. 53PCh. 9 - The vector position of a 3.50-g particle moving in...Ch. 9 - Prob. 55PCh. 9 - Prob. 56PCh. 9 - Prob. 57PCh. 9 - Prob. 58PCh. 9 - Prob. 59PCh. 9 - Prob. 60PCh. 9 - A garden hose is held as shown in Figure P9.32....Ch. 9 - Prob. 62PCh. 9 - Prob. 63PCh. 9 - A rocket has total mass Mi = 360 kg, including...Ch. 9 - A ball of mass m is thrown straight up into the...Ch. 9 - Prob. 66APCh. 9 - A 3.00-kg steel ball strikes a wall with a speed...Ch. 9 - (a) Figure P9.36 shows three points in the...Ch. 9 - Review. A 60.0-kg person running at an initial...Ch. 9 - A cannon is rigidly attached to a carriage, which...Ch. 9 - A 1.25-kg wooden block rests on a table over a...Ch. 9 - A wooden block of mass M rests on a table over a...Ch. 9 - Prob. 73APCh. 9 - Prob. 74APCh. 9 - Two gliders are set in motion on a horizontal air...Ch. 9 - Why is the following situation impossible? An...Ch. 9 - Prob. 77APCh. 9 - Prob. 78APCh. 9 - Prob. 79APCh. 9 - A small block of mass m1 = 0.500 kg is released...Ch. 9 - Review. A bullet of mass m = 8.00 g is fired into...Ch. 9 - Review. A bullet of mass m is fired into a block...Ch. 9 - A 0.500-kg sphere moving with a velocity expressed...Ch. 9 - Prob. 84APCh. 9 - Prob. 85APCh. 9 - Prob. 86APCh. 9 - Review. A light spring of force constant 3.85 N/m...Ch. 9 - Prob. 88APCh. 9 - Prob. 89APCh. 9 - Prob. 90APCh. 9 - Prob. 91APCh. 9 - Prob. 92CPCh. 9 - Prob. 93CPCh. 9 - Sand from a stationary hopper falls onto a moving...Ch. 9 - On a horizontal air track, a glider of mass m...Ch. 9 - Prob. 96CP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- 1. A charge of -25 μC is distributed uniformly throughout a spherical volume of radius 11.5 cm. Determine the electric field due to this charge at a distance of (a) 2 cm, (b) 4.6 cm, and (c) 25 cm from the center of the sphere. (a) = = (b) E = (c)Ẻ = = NC NC NCarrow_forward1. A long silver rod of radius 3.5 cm has a charge of -3.9 ис on its surface. Here ŕ is a unit vector ст directed perpendicularly away from the axis of the rod as shown in the figure. (a) Find the electric field at a point 5 cm from the center of the rod (an outside point). E = N C (b) Find the electric field at a point 1.8 cm from the center of the rod (an inside point) E=0 Think & Prepare N C 1. Is there a symmetry in the charge distribution? What kind of symmetry? 2. The problem gives the charge per unit length 1. How do you figure out the surface charge density σ from a?arrow_forward1. Determine the electric flux through each surface whose cross-section is shown below. 55 S₂ -29 S5 SA S3 + 9 Enter your answer in terms of q and ε Φ (a) s₁ (b) s₂ = -29 (C) Φ զ Ερ (d) SA = (e) $5 (f) Sa $6 = II ✓ -29 S6 +39arrow_forward
- No chatgpt pls will upvotearrow_forwardthe cable may break and cause severe injury. cable is more likely to break as compared to the [1] ds, inclined at angles of 30° and 50° to the vertical rings by way of a scaled diagram. [4] I 30° T₁ 3cm 3.8T2 cm 200 N 50° at it is headed due North and its airspeed indicat 240 km/h. If there is a wind of 100 km/h from We e relative to the Earth? [3]arrow_forwardCan you explain this using nodal analysis With the nodes I have present And then show me how many KCL equations I need to write, I’m thinking 2 since we have 2 dependent sourcesarrow_forward
- The shear leg derrick is used to haul the 200-kg net of fish onto the dock as shown in. Assume the force in each leg acts along its axis. 5.6 m. 4 m- B Part A Determine the compressive force along leg AB. Express your answer to three significant figures and include the appropriate units. FAB = Value Submit Request Answer Part B Units ? Determine the compressive force along leg CB. Express your answer to three significant figures and include the appropriate units. FCB= Value Submit Request Answer Part C ? Units Determine the tension in the winch cable DB. Express your answer with the appropriate units. 2marrow_forwardPart A (Figure 1) shows a bucket suspended from a cable by means of a small pulley at C. If the bucket and its contents have a mass of 10 kg, determine the location of the pulley for equilibrium. The cable is 6 m long. Express your answer to three significant figures and include the appropriate units. Figure 4 m B НА x = Value Submit Request Answer Provide Feedback < 1 of 1 T 1 m Units ?arrow_forwardThe particle in is in equilibrium and F4 = 165 lb. Part A Determine the magnitude of F1. Express your answer in pounds to three significant figures. ΑΣΦ tvec F₁ = Submit Request Answer Part B Determine the magnitude of F2. Express your answer in pounds to three significant figures. ΑΣΦ It vec F2 = Submit Request Answer Part C Determine the magnitude of F3. Express your answer in pounds to three significant figures. ? ? lb lb F₂ 225 lb 135° 45° 30° -60°-arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
Impulse Derivation and Demonstration; Author: Flipping Physics;https://www.youtube.com/watch?v=9rwkTnTOB0s;License: Standard YouTube License, CC-BY