Statics and Mechanics of Materials (5th Edition)
5th Edition
ISBN: 9780134382593
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 8.6, Problem 28P
The shear stress-strain diagram for an alloy is shown in the figure. If a bolt having a diameter of 0.25 in. is made of this material and used in the lap joint, determine the modulus of elasticity E and the force P required to cause the material to yield, Take v = 0.3.
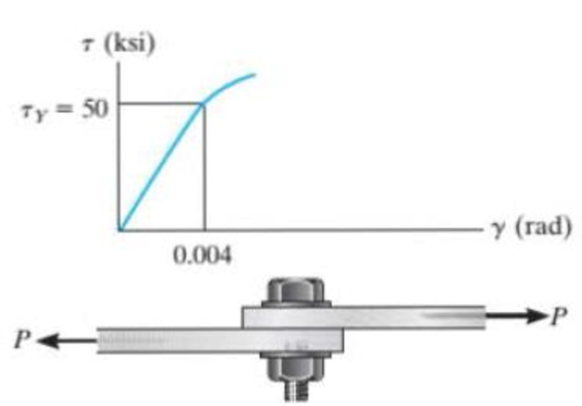
Prob. 8-28.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
PLEASE SOLVE STEP BY STEP WITHOUT ARTIFICIAL INTELLIGENCE OR CHATGPT
SOLVE BY HAND STEP BY STEP
PLEASE SOLVE STEP BY STEP WITHOUT ARTIFICIAL INTELLIGENCE OR CHATGPT
SOLVE BY HAND STEP BY STEP
PLEASE SOLVE STEP BY STEP WITHOUT ARTIFICIAL INTELLIGENCE OR CHATGPT
SOLVE BY HAND STEP BY STEP
Chapter 8 Solutions
Statics and Mechanics of Materials (5th Edition)
Ch. 8.4 - Define a homogeneous material.Ch. 8.4 - Prob. 2FPCh. 8.4 - Prob. 3FPCh. 8.4 - Prob. 4FPCh. 8.4 - Prob. 5FPCh. 8.4 - As the temperature increases the modulus of...Ch. 8.4 - Prob. 7FPCh. 8.4 - Prob. 8FPCh. 8.4 - Prob. 9FPCh. 8.4 - Prob. 10FP
Ch. 8.4 - The material for the 50-mm-long specimen has the...Ch. 8.4 - If the elongation of wire BC is 0.2 mm after the...Ch. 8.4 - A tension test was performed on a steel specimen...Ch. 8.4 - Data taken from a stressstrain test for a ceramic...Ch. 8.4 - Data taken from a stressstrain test for a ceramic...Ch. 8.4 - Prob. 4PCh. 8.4 - The stress-strain diagram for a steel alloy having...Ch. 8.4 - Prob. 6PCh. 8.4 - The rigid beam is supported by a pin at C and an...Ch. 8.4 - The rigid beam is supported by a pin at C and an...Ch. 8.4 - Prob. 9PCh. 8.4 - The stressstrain diagram for an aluminum alloy...Ch. 8.4 - The stressstrain diagram for an aluminum alloy...Ch. 8.4 - Prob. 12PCh. 8.4 - A bar having a length of 5 in. and cross-sectional...Ch. 8.4 - The rigid pipe is supported by a pin at A and an...Ch. 8.4 - The rigid pipe is supported by a pin at A and an...Ch. 8.4 - Prob. 16PCh. 8.4 - The rigid beam is supported by a pin at C and an...Ch. 8.4 - Prob. 18PCh. 8.4 - Prob. 19PCh. 8.6 - A 100 mm long rod has a diameter of 15 mm. If an...Ch. 8.6 - A solid circular rod that is 600 mm long and 20 mm...Ch. 8.6 - Prob. 15FPCh. 8.6 - Prob. 16FPCh. 8.6 - The acrylic plastic rod is 200 mm long and 15 mm...Ch. 8.6 - The plug has a diameter of 30 mm and fits within a...Ch. 8.6 - The elastic portion of the stress-strain diagram...Ch. 8.6 - The elastic portion of the stress-strain diagram...Ch. 8.6 - The brake pads for a bicycle tire arc made of...Ch. 8.6 - The lap joint is connected together using a 1.25...Ch. 8.6 - The lap joint is connected together using a 1.25...Ch. 8.6 - Prob. 27PCh. 8.6 - The shear stress-strain diagram for an alloy is...Ch. 8.6 - Prob. 29PCh. 8 - The elastic portion of the tension stress-strain...Ch. 8 - Prob. 2RPCh. 8 - Prob. 3RPCh. 8 - Prob. 4RPCh. 8 - Prob. 5RPCh. 8 - Prob. 6RPCh. 8 - The stress-strain diagram for polyethylene, which...Ch. 8 - The pipe with two rigid caps attached to its ends...Ch. 8 - Prob. 9RPCh. 8 - Prob. 10RP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Consider the bar, shown in Figure 1 that undergoes axial displacement due to both a distributed load and a point force. The bar is of cross-sectional area A = 1.10-3 m², and has a modulus of elasticity E = 100 GPa. 1(x) = 5 kN/m x=0.0 x=2.0 2.0m 10 kN Figure 1: Bar domain with varying distributed forces. a) The general form of the governing equations describing the bar's displacement, u(x), is given by, d (AE du(x)) -) +1(x) = 0. d.x dx What are the accompanying boundary conditions for this bar? b) Using the mesh in Figure 2, form the basis functions associated with element 2 and write the FEM approximation over the element. 1 2 3 1 2 1m 1m Figure 2: Mesh of 2 elements. Elements are numbered with underlines. c) The general form of the element stiffness matrix system, with nodes indexed by i and j, is, AE Uj N;(x)l(x)dx – Ng(0)f(0) ¥ [4]}]{{}}={{{}\(\\+} + {N(2)f(2) = N (0)5() }, (1) 0, respectively. L = (2) where f(2) and f(0) denote the boundary forces at positions x 2 and x Evaluate…arrow_forwardanswer pleasearrow_forwardamination) Question 1 Consider the bar, shown in Figure 1, that undergoes axial displacement due to both a distributed load and a point force. The bar is of cross-sectional area A = 1.103 m2, and has a modulus of elasticity E = 100 GPa. 1(x) = 5 kN/m 10 kN X x=0.0 x=2.0 2.0m Figure 1: Bar domain with varying distributed forces. a) The general form of the governing equations describing the bar's displacement, u(x), is given by, d (AE du(x)) + 1(x) = 0. dx dx What are the accompanying boundary conditions for this bar? MacBook Air a 会 DII F5 F6 F7 F8 80 F3 F4 0/ 20 [8 marksl 8 FOarrow_forward
- show workingarrow_forwardCFD help Figure 3: Advection equation, solution for three different timesteps. Q1) Provide an explanation what conditions and numerical setup could explain the curves. Identify which of the three curves is the first, second and third timestep.arrow_forwardanswer pleasearrow_forward
- Figure 3 shows the numerical solution of the advection equation for a scalar u along x at three consecutive timesteps. 1.0 0.8- 0.6 0.4- 0.2 0.0 00 -0.2 -0.4 -0.6- 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 Figure 3: Advection equation, solution for three different timesteps.arrow_forwardQuestion 2 Figure 3 shows the numerical solution of the advection equation for a scalar u along x at three consecutive timesteps. 1.0 0.8- 0.6- 0.4- 0.2- 0.0- -0.2- -0.4- -0.6 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 Figure 3: Advection equation, solution for three different timesteps. a) Provide an explanation what conditions and numerical setup could explain the curves. Identify which of the three curves is the first, second and third timestep. b) Consider explicit schemes with central and upwind discretisations. Explain how each of these candidate discretisations could produce the behaviour shown in Figure 3. c) Determine the CFL number that was used in the simulation for each of the candidate schemes for all possible updates. Assume that the timestep and mesh-width used are constant. Read the data to two digits of accuracy from Figure 4 shown at the end of the question, which is an enlarged version of Figure 3. Demonstrate your method and input data for one calculation, but then use a…arrow_forwardanswer pleasearrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
EVERYTHING on Axial Loading Normal Stress in 10 MINUTES - Mechanics of Materials; Author: Less Boring Lectures;https://www.youtube.com/watch?v=jQ-fNqZWrNg;License: Standard YouTube License, CC-BY