Chapter 8, Problem 1RP

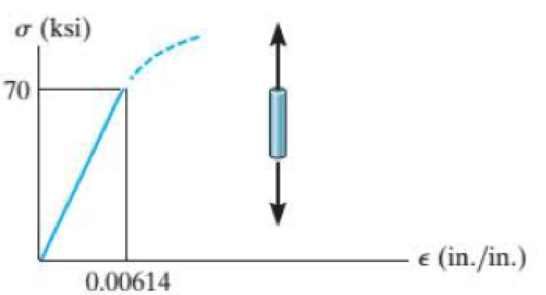
The elastic portion of the tension stress-strain diagram for an aluminum alloy is shown in the figure. The specimen used for the test has a gage length of 2 in. and a diameter of 0,5 in. When the applied load is 9 kip, the new diameter of the specimen is 0.49935 in. Calculate the shear modulus G_al for the aluminum.

Probs. R8-1/2

To determine

Find the shear modulus for an aluminum alloy

Answer to Problem 1RP

The shear modulus for an aluminum alloy is $\underset{\_}{\text{4}\text{.31}\times {\text{10}}^3\text{ksi}}$.

Explanation of Solution

Given information:

Gage length is 2 in..

The diameter of the specimen is 0.5 in..

The axial load acts on the specimen is 9 kips..

The new diameter of the specimen is 0.49935 in.

Calculation:

Calculate the modulus of elasticity for aluminum $\left(E_{\text{al}}\right)$ using the relation as shown below:

$E_{\text{al}}=\frac{\sigma }{\epsilon }$

Here, the stress is $\sigma$ and the strain is $\epsilon$.

Refer the stress-strain diagram.

The value of stress is 70 ksi and the value of strain is $0.00614\frac{\text{in}\text{.}}{\text{in}\text{.}}$.

Substitute 70 ksi for $\sigma$ and $0.00614\frac{\text{in}\text{.}}{\text{in}\text{.}}$ for $\epsilon$.

$\begin{array}{c}{E}_{\text{al}}=\frac{70}{0.00614}\\ =11400.65\text{ksi}\end{array}$

The expression to find the cross-sectional area of the specimen $\left(A\right)$ is shown below:

$A=\frac{\pi }{4}{d}^2$

Here, the diameter of the specimen is d.

Substitute 0.5 in. for d.

$\begin{array}{c}A=\frac{\pi }{4}{\left(0.5\right)}^2\\ =0.19635{\text{in}}^{\text{2}}\end{array}$

Find the value of stress when the specimen is loaded with a 9 kip load using the relation:

$\sigma =\frac{P}{A}$

Here, the load is P.

Substitute 9 kip for P and $0.19635{\text{in}}^{\text{2}}$ for A.

$\begin{array}{c}\sigma =\frac{9}{0.19635}\\ =45.84\text{ksi}\end{array}$

The expression to find the strain in the longitudinal or axial direction $\left({\epsilon }_{\text{long}}\right)$ using Hook’s law is shown below:

${\epsilon }_{\text{long}}=\frac{\sigma }{E}$

Here, the Young’s modulus of the aluminum is E.

Substitute 45.84 ksi for $\sigma$ and 11,400.65 ksi for E.

$\begin{array}{c}{\epsilon }_{\text{long}}=\frac{\text{45}\text{.84}}{11400.65}\\ =0.0040208\frac{\text{in}\text{.}}{\text{in}\text{.}}\end{array}$

Find the strain in lateral direction $\left({\epsilon }_{\text{lat}}\right)$ using the relation as shown below:

${\epsilon }_{\text{lat}}=\frac{d\text{'}-d}{d}$

Here, the new diameter is $d\text{'}$ and the initial diameter is d.

Substitute 0.49935 in. for $d\text{'}$ and 0.5 in. for d.

$\begin{array}{c}{\epsilon }_{\text{lat}}=\frac{0.49935-0.5}{0.5}\\ =-0.0013\frac{\text{in}\text{.}}{\text{in}\text{.}}\end{array}$

Find the Poisson’s ratio $\left(\nu \right)$ using the relation as shown below:

$\nu =-\frac{{\epsilon }_{\text{lat}}}{{\epsilon }_{\text{long}}}$

Substitute $-0.0013\frac{\text{in}\text{.}}{\text{in}\text{.}}$ for ${\epsilon }_{\text{lat}}$ and $0.0040208\frac{\text{in}\text{.}}{\text{in}\text{.}}$ for ${\epsilon }_{\text{long}}$.

$\begin{array}{c}\nu =-\frac{-0.0013}{0.0040208}\\ =0.32332\end{array}$

Calculate the modulus of rigidity for the specimen $\left(G_{\text{al}}\right)$ using the relation as shown below:

$G_{\text{al}}=\frac{E_{\text{al}}}{2\left(1+\nu \right)}$

Substitute 11,400.65 ksi for $E_{\text{al}}$ and 0.32332 for $\nu$.

$\begin{array}{c}{G}_{\text{al}}=\frac{11400.65}{2\left(1+0.32332\right)}\\ =4307.594\text{ksi}\\ \text{= 4}\text{.31}\times {\text{10}}^3\text{ksi}\end{array}$

Therefore, the shear modulus for an aluminum alloy is $\underset{\_}{\text{4}\text{.31}\times {\text{10}}^3\text{ksi}}$.