Chapter 8, Problem 8.5.24P

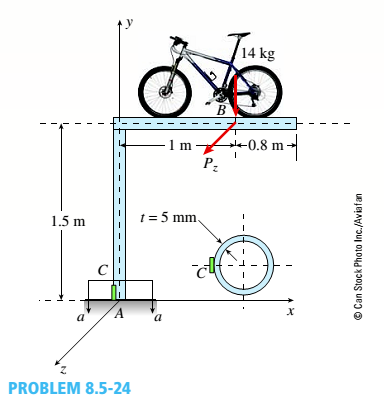
Repeat Problem 8.5-22 but replace the square tube column with a circular tube having a wall thickness r = 5 mm and the same cross-sectional area (3900 mm²) as that of the square tube in figure b in Problem 8.5-22. Also, add force P. = 120 N at B

(a) Find the state of plane stress at C. (b) Find maximum normal stresses and show them on a sketch of a properly oriented element.

(c) Find maximum shear stresses and show them on a sketch of a properly oriented element.

  

To determine

The state of plane stress on an element C.

Answer to Problem 8.5.24P

The state of stress on element C are

Tensile stress ${\sigma }_t=0.499\text{MPa}$

Compressive stress ${\sigma }_c=-0.5694\text{MPa}$

Explanation of Solution

Given information:

The cross-section of the bicycle rack tubing is circular.

The weight of the bicycle = 14 kg is represented as point load applied at B on a plane frame model of the rack.

A force in z direction has also been added P_z= 120 N

Weight density of the steel $\gamma =77{\text{kN/m}}^{\text{3}}$

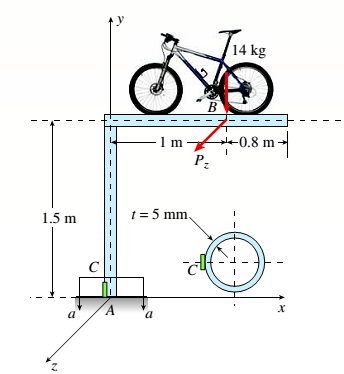
Calculation:

From the figure, let us consider horizontal portion of the cycle rack. The weight of the cycle is considered as the point load and this load produces a moment and a direct compressive load in the beam along Y-direction.

Also, a load P_zhas been added in z direction. This load will produce bending moment in the horizontal beam and twisting moment in the vertical portion of the beam.

The cross-sectional area of the beam is given by

  $A=3900m{m}^2=3.9\times {10}^{-3}{m}^2$

  $\begin{array}{l}A=\frac{\pi }{4}\left(d^2-{\left(d-t\right)}^2\right)\\ 3900=\frac{\pi }{4}\left(d^2-{\left(d-5\right)}^2\right)\end{array}$

  $d=499.06mm$

The moment in the vertical beam =

  $\begin{array}{l}M=14\times 9.81\times 1\\ M=137.34\text{N}\cdot \text{m}\end{array}$

The moment in the horizontal beam due to load P_z= $M_z=P_z\times 1m$

  $M_z=120\times 1=120\text{Nm}$

Total moment $M_e=137.34+120=257.34\text{Nm}$

The load P_zwill produce twisting moment equal to M_z. This twisting moment will produce the shear stress at the base of rack.

The direct compressive loading = $P=14\times 9.81=137.34\text{N}$

From the properties of the cross-section, the moment of inertia is

  $I=\frac{\pi d^4}{64}-\frac{\pi {\left(d-t\right)}^4}{64}$

  $I=\frac{\pi \times {\left(499.06\right)}^4}{64}-\frac{\pi \times {\left(499.06-5\right)}^4}{64}$

  $\begin{array}{l}I=1.202\times {10}^{8}m{m}^4\\ I=1.202\times {10}^{-4}{m}^4\end{array}$

Now, plane stress can be calculated as follows

  ${\sigma }_t=-\frac{P}{A}+\frac{M\times \left(\frac{d}{2}\right)}{I}$

  ${\sigma }_t=-\frac{14\times 9.81}{39\times {10}^{-4}}+\frac{257.34\times \left(\frac{499.06\times {10}^{-3}}{2}\right)}{1.202\times {10}^{-4}}$

  ${\sigma }_t=0.499\text{MPa}$

And maximum compressive stress is

  ${\sigma }_c=-\frac{P}{A}-\frac{M\times \left(\frac{a}{2}\right)}{I}$

  ${\sigma }_c=-\frac{14\times 9.81}{39\times {10}^{-4}}-\frac{257.34\times \left(\frac{499.06\times {10}^{-3}}{2}\right)}{1.202\times {10}^{-4}}$

  ${\sigma }_c=-0.5694\text{MPa}$

Conclusion: Thus, the state of stress on element C are

Tensile stress ${\sigma }_t=0.499\text{MPa}$

Compressive stress ${\sigma }_c=-0.5694\text{MPa}$

To determine

The maximum normal stress and the sketch of properly oriented element.

Answer to Problem 8.5.24P

The normal stress values on element C are, ${\sigma }_1=0.094166\text{MPa}$ , ${\sigma }_2=-0.1646\text{MPa}$ .

Explanation of Solution

Given information:

The cross-section of the bicycle rack tubing is circular.

The weight of the bicycle = 14 kg is represented as point load applied at B on a plane frame model of the rack.

A force in z direction has also been added P_z= 120 N

Weight density of the steel $\gamma =77{\text{kN/m}}^{\text{3}}$

Calculation:

From the figure, let us consider horizontal portion of the cycle rack. The weight of the cycle is considered as the point load and this load produces a moment and a direct compressive load in the beam along Y-direction.

Also, a load P_zhas been added in z direction. This load will produce bending moment in the horizontal beam and twisting moment in the vertical portion of the beam.

The cross-sectional area of the beam is given by

  $A=3900m{m}^2=3.9\times {10}^{-3}{m}^2$

  $\begin{array}{l}A=\frac{\pi }{4}\left(d^2-{\left(d-t\right)}^2\right)\\ 3900=\frac{\pi }{4}\left(d^2-{\left(d-5\right)}^2\right)\end{array}$

  $d=499.06mm$

The moment in the vertical beam =

  $\begin{array}{l}M=14\times 9.81\times 1\\ M=137.34\text{N}\cdot \text{m}\end{array}$

The moment in the horizontal beam due to load P_z= $M_z=P_z\times 1m$

  $M_z=120\times 1=120\text{Nm}$

Total moment $M_e=137.34+120=257.34\text{Nm}$

The load P_zwill produce twisting moment equal to M_z. This twisting moment will produce the shear stress at the base of rack.

The direct compressive loading = $P=14\times 9.81=137.34\text{N}$

From the properties of the cross-section, the moment of inertia is

  $I=\frac{\pi d^4}{64}-\frac{\pi {\left(d-t\right)}^4}{64}$

  $I=\frac{\pi \times {\left(499.06\right)}^4}{64}-\frac{\pi \times {\left(499.06-5\right)}^4}{64}$

  $\begin{array}{l}I=1.202\times {10}^{8}m{m}^4\\ I=1.202\times {10}^{-4}{m}^4\end{array}$

Now, plane stress can be calculated as follows

  ${\sigma }_t=-\frac{P}{A}+\frac{M\times \left(\frac{d}{2}\right)}{I}$

  ${\sigma }_t=-\frac{14\times 9.81}{39\times {10}^{-4}}+\frac{257.34\times \left(\frac{499.06\times {10}^{-3}}{2}\right)}{1.202\times {10}^{-4}}$

  ${\sigma }_t=0.499\text{MPa}$

And maximum compressive stress is

  ${\sigma }_c=-\frac{P}{A}-\frac{M\times \left(\frac{a}{2}\right)}{I}$

  ${\sigma }_c=-\frac{14\times 9.81}{39\times {10}^{-4}}-\frac{257.34\times \left(\frac{499.06\times {10}^{-3}}{2}\right)}{1.202\times {10}^{-4}}$

  ${\sigma }_c=-0.5694\text{MPa}$

The shear stress on the element is given by the torque and shear stress relation.

  $\tau =\frac{16\times T\times d}{\pi \left(d^4-{\left(d-t\right)}^4\right)}$

  $\tau =\frac{16\times 120\times 0.499}{\pi \left({\left(0.499\right)}^4-{\left(0.499-\left(5\times {10}^{-3}\right)\right)}^4\right)}$

  $\tau =0.124581MPa$

The normal stresses are given by

  ${\sigma }_{1,2}=\frac{{\sigma }_x+{\sigma }_y}{2}\pm \frac{1}{2}\sqrt{{\left({\sigma }_x-{\sigma }_y\right)}^2+4{\tau }_{xy}{}^2}$

  ${\sigma }_{1,2}=\frac{0.499-0.56944}{2}\pm \frac{1}{2}\sqrt{{\left(0.499-0.56944\right)}^2+4\times {\left(0.1245\right)}^2}$

  ${\sigma }_1=0.094166\text{MPa}$

And,

  ${\sigma }_2=-0.1646\text{MPa}$

The state of stress on the element can be shown as follows

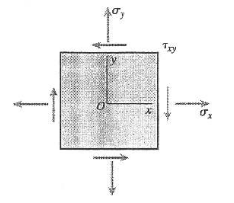
Conclusion: Thus, the normal stress values on element C are, ${\sigma }_1=0.094166\text{MPa}$ , ${\sigma }_2=-0.1646\text{MPa}$ .

To determine

The maximum shear stress and the sketch of properly oriented element.

Answer to Problem 8.5.24P

the maximum stress values on element C is $\tau =0.129383\text{MPa}$ .

Explanation of Solution

Given information:

The cross-section of the bicycle rack tubing is circular.

The weight of the bicycle = 14 kg is represented as point load applied at B on a plane frame model of the rack.

A force in z direction has also been added P_z= 120 N

Weight density of the steel $\gamma =77{\text{kN/m}}^{\text{3}}$

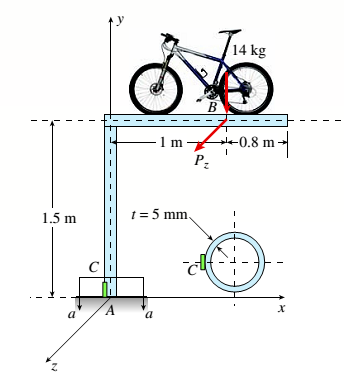
Calculation:

From the figure, let us consider horizontal portion of the cycle rack. The weight of the cycle is considered as the point load and this load produces a moment and a direct compressive load in the beam along Y-direction.

Also, a load P_zhas been added in z direction. This load will produce bending moment in the horizontal beam and twisting moment in the vertical portion of the beam.

The cross-sectional area of the beam is given by

  $A=3900m{m}^2=3.9\times {10}^{-3}{m}^2$

  $\begin{array}{l}A=\frac{\pi }{4}\left(d^2-{\left(d-t\right)}^2\right)\\ 3900=\frac{\pi }{4}\left(d^2-{\left(d-5\right)}^2\right)\end{array}$

  $d=499.06mm$

The moment in the vertical beam =

  $\begin{array}{l}M=14\times 9.81\times 1\\ M=137.34\text{N}\cdot \text{m}\end{array}$

The moment in the horizontal beam due to load P_z= $M_z=P_z\times 1m$

  $M_z=120\times 1=120\text{Nm}$

Total moment $M_e=137.34+120=257.34\text{Nm}$

The load P_zwill produce twisting moment equal to M_z. This twisting moment will produce the shear stress at the base of rack.

The direct compressive loading = $P=14\times 9.81=137.34\text{N}$

From the properties of the cross-section, the moment of inertia is

  $I=\frac{\pi d^4}{64}-\frac{\pi {\left(d-t\right)}^4}{64}$

  $I=\frac{\pi \times {\left(499.06\right)}^4}{64}-\frac{\pi \times {\left(499.06-5\right)}^4}{64}$

  $\begin{array}{l}I=1.202\times {10}^{8}m{m}^4\\ I=1.202\times {10}^{-4}{m}^4\end{array}$

Now, plane stress can be calculated as follows

  ${\sigma }_t=-\frac{P}{A}+\frac{M\times \left(\frac{d}{2}\right)}{I}$

  ${\sigma }_t=-\frac{14\times 9.81}{39\times {10}^{-4}}+\frac{257.34\times \left(\frac{499.06\times {10}^{-3}}{2}\right)}{1.202\times {10}^{-4}}$

  ${\sigma }_t=0.499\text{MPa}$

And maximum compressive stress is

  ${\sigma }_c=-\frac{P}{A}-\frac{M\times \left(\frac{a}{2}\right)}{I}$

  ${\sigma }_c=-\frac{14\times 9.81}{39\times {10}^{-4}}-\frac{257.34\times \left(\frac{499.06\times {10}^{-3}}{2}\right)}{1.202\times {10}^{-4}}$

  ${\sigma }_c=-0.5694\text{MPa}$

The shear stress on the element is given by the torque and shear stress relation.

  $\tau =\frac{16\times T\times d}{\pi \left(d^4-{\left(d-t\right)}^4\right)}$

  $\tau =\frac{16\times 120\times 0.499}{\pi \left({\left(0.499\right)}^4-{\left(0.499-\left(5\times {10}^{-3}\right)\right)}^4\right)}$

  $\tau =0.124581MPa$

The normal stresses are given by

  ${\sigma }_{1,2}=\frac{{\sigma }_x+{\sigma }_y}{2}\pm \frac{1}{2}\sqrt{{\left({\sigma }_x-{\sigma }_y\right)}^2+4{\tau }_{xy}{}^2}$

  ${\sigma }_{1,2}=\frac{0.499-0.56944}{2}\pm \frac{1}{2}\sqrt{{\left(0.499-0.56944\right)}^2+4\times {\left(0.1245\right)}^2}$

  ${\sigma }_1=0.094166\text{MPa}$

And,

  ${\sigma }_2=-0.1646\text{MPa}$

The in plane maximum shear stress value is given by

  $\tau =\left|\frac{{\sigma }_1-{\sigma }_2}{2}\right|$

  $\begin{array}{l}\tau =\frac{0.094166-\left(-0.1646\right)}{2}\\ \tau =0.129383\text{MPa}\end{array}$

The state of stress on the element can be shown as follows

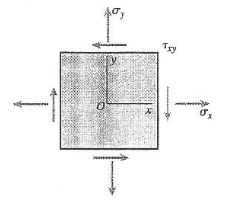
Conclusion: Thus, the maximum stress values on element C is $\tau =0.129383\text{MPa}$ .