Chapter 8, Problem 76E

Refer to the circuit of Fig. 8.95, which contains a voltage-controlled dependent voltage source in addition to two resistors. (a) Compute the circuit time constant. (b) Obtain an expression for v_x valid for all t. (c) Plot the power dissipated in the 4 Ω resistor over the range of six time constants. (d) Repeat parts (a) to (c) if the dependent source is installed in the circuit upside down. (e) Are both circuit configurations “stable”? Explain.

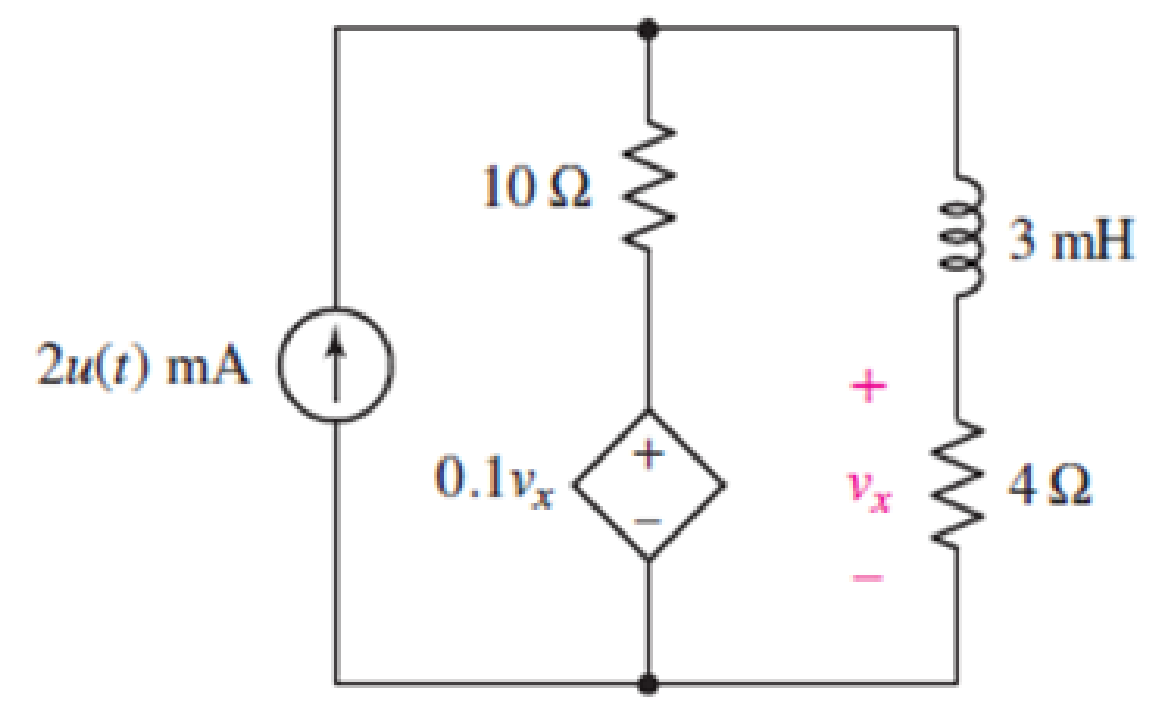
Figures 8.95

To determine

Find the circuit time constant.

Answer to Problem 76E

The time constant of the circuit is $220.6\mu \text{s}$.

Explanation of Solution

Formula used:

The expression for the resistance of the circuit is as follows:

$R=\frac{v}{i}$ (1)

Here,

$R$ is the resistance,

$v$ is the voltage and

$i$ is the current.

The expression for the time constant of circuit is as follows:

$\tau =\frac{L}{R_{eq}}$ (2)

Here,

$\tau$ is the circuit time constant,

$R_{eq}$ is the equivalent resistance across inductor and

$L$ is the inductance of the inductor.

Calculation:

To find equivalent resistance of a circuit the independent current source is replaced by open circuit and $1\text{V}$ test source is connected across open circuit terminal.

The circuit diagram is redrawn as shown in Figure 1.

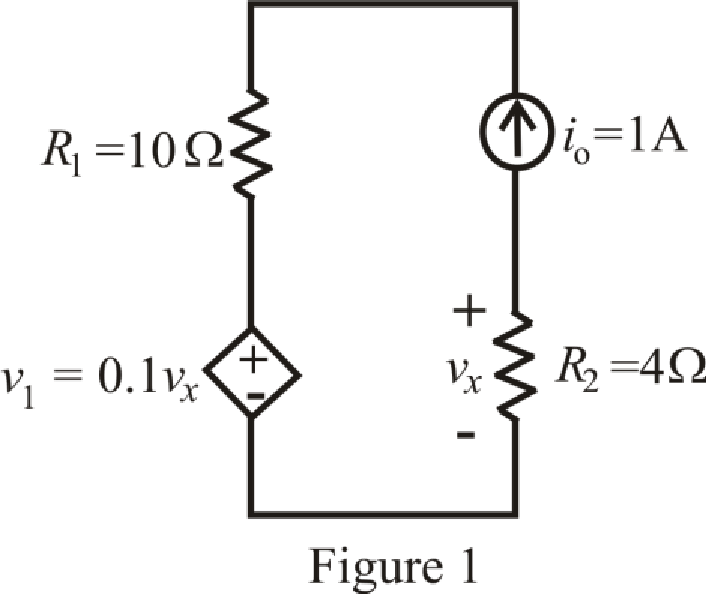
Refer to the redrawn Figure 1:

Apply KVL in mesh 1:

$-v_1+i_1{R}_1+v_0+i_1{R}_2=0$ (3)

Here,

$v_1$ is the voltage of $0.1v_x$ dependent source,

$v_0$ are the voltage of $1\text{V}$ test source,

$i_1$ is the current flowing in mesh 1 and

$R_1$ is the resistance of $10\Omega$ resistor and

$R_2$ is the resistance of $4\Omega$ resistor.

Substitute $0.1v_x$ for $v_1$, $10\text{Ω}$ for $R_1$, $4\text{Ω}$ for $R_2$ and $1\text{V}$ for $v_0$ in equation (3):

$-0.1v_x+\left(10\text{Ω}\right)i_1+1\text{V}+\left(4\text{Ω}\right)i_1=0$

$-0.1v_x+14i_1+1\text{V}=0$ (3)

The expression for voltage across the $4\text{Ω}$ resistor is as follows:

$v_x=i_1{R}_2$ (4)

Here,

$v_x$ is voltage across resistor $4\text{Ω}$ resistor.

Substitute $4\text{Ω}$ for $R_2$ in equation (5):

$v_x=i_1\left(4\text{Ω}\right)$

Substitute $i_1\left(4\text{Ω}\right)$ for $v_x$ in equation (4):

$\begin{array}{l}-0.1\left(i_1\left(4\text{Ω}\right)\right)+14i_1+1\text{V}=0\\ -0.4i_1+14i_1+1\text{V}=0\end{array}$

$-13.6i_1+1\text{V}=\text{0}$ (6)

Rearrange for $i_1$:

$\begin{array}{l}13.6i_1=1\text{V}\\ i_1=0.07353\text{A}\end{array}$

Substitute $1\text{V}$ for $v$ and $0.07353\text{A}$ for $i$ in equation (1):

$\begin{array}{c}R=\frac{1\text{V}}{0.07353\text{A}}\\ =13.6\text{Ω}\end{array}$

So, the equivalent resistance across inductor is $13.6\text{Ω}$.

Substitute $13.6\text{Ω}$ for $R_{eq}$ and $\text{3 mH}$ for $L$ in equation (2):

$\begin{array}{c}\tau =\frac{\text{3 mH}}{13.6\text{Ω}}\\ =\frac{\text{3}}{13.6}\text{s}\\ =0.2206\text{ms}\\ =220.6\mu \text{s}\left\{\because 1\text{ms}={10}^3\mu \text{s}\right\}\end{array}$

So the time constant of the circuit is $220.6\mu \text{s}$.

Conclusion:

Thus, the time constant of the circuit is $220.6\mu \text{s}$.

To determine

Obtain an expression for $v_x$ valid for all $t$.

Answer to Problem 76E

The expression for the voltage $v_x$ valid for all $t$ is $5.88\left(1-e^{-\frac{t}{220.6\mu \text{s}}}\right)\text{V}$.

Explanation of Solution

Formula used:

The expression for the final response of the circuit valid for all $t$ is as follows:

$i\left(t\right)=i\left(\infty \right)+\left(i\left(0-i\left(\infty \right)\right)\right)e^{-\frac{t}{\tau }}$ (7)

Here,

$i\left(t\right)$ is the final response of the circuit valid for all $t$,

$i\left(\infty \right)$ is the current flowing in the circuit for $t=\infty$,

$i\left(0\right)$ is the current flowing in the circuit for $t=0^{-}$ and

$t$ is the time.

Calculation:

The unit-step forcing function as a function of time which is zero for all values of its argument less than zero and which is unity for all positive values of its argument.

$u\left(t-t_0\right)=\{\begin{array}{l}0t<t_0\\ 1t>t_0\end{array}$

Here,

$t_0$ is the point at which argument of unit step function becomes zero.

The independent current source is:

$i=2u\left(t\right)\text{ A}$ (8)

Substitute $0^{-}$ for $t$ in equation (8):

$\begin{array}{c}{i}_{0^{-}}=2u\left(0^{-}\right)\text{ A}\\ =2\left(0\right)\text{ A}\\ =\text{0}\text{A}\end{array}$

The current through $2u\left(t\right)\text{ A}$  independent current source is $0\text{A}$.

The $2u\left(t\right)\text{ A}$ independent current source behaves as open circuited and therefore no current flows in the circuit.

So, the value of the current flowing through the inductor for $t=0^{-}$ is $0\text{A}$.

The inductor does not allow sudden change in the current.

So,

$i\left(0^{+}\right)=i\left(0^{-}\right)$

Therefore, the current flowing in the circuit for $t=0$ is $0\text{A}$.

Substitute $\infty$ for $t$ in equation (8),

$\begin{array}{c}{i}_{\infty }=2u\left(\infty \right)\text{ A}\\ =2\left(1\right)\text{ A}\\ =2\text{A}\end{array}$

So, the current flowing through the $2u\left(t\right)\text{ A}$ independent current source for $t=\infty$ is $2\text{A}$.

The circuit diagram is redrawn as shown in Figure 2 for $t=\infty$.

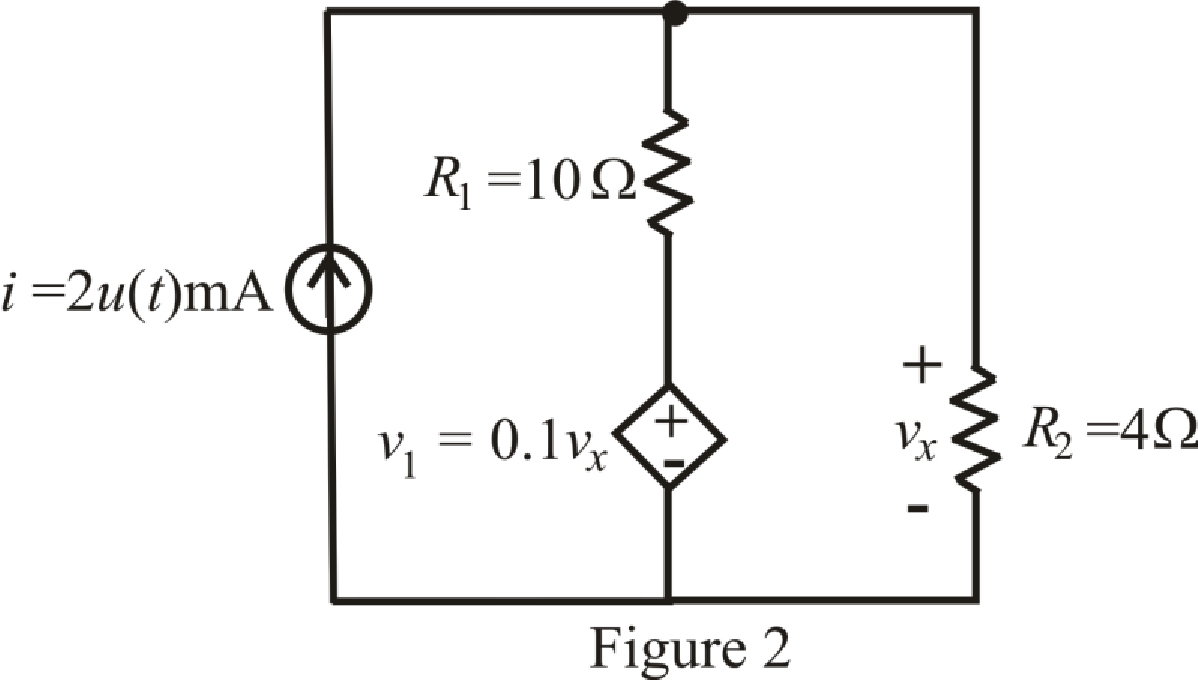
Refer to the redrawn Figure 2:

Apply KCL in the circuit:

$\frac{v_x-v_1}{R_1}+\frac{v_x}{R_2}=i$ (9)

Substitute $0.1v_x$ for $v_1$, $10\text{Ω}$ for $R_1$, $4\text{Ω}$ for $R_2$ and $2\text{A}$ for $i$ in equation (9):

$\begin{array}{l}\frac{v_x-0.1v_x}{10\text{Ω}}+\frac{v_x}{4\text{Ω}}=2\text{A}\\ \frac{2v_x-0.2v_x+5v_x}{20\text{Ω}}=2\text{A}\\ \frac{6.8v_x}{20\text{Ω}}=2\text{A}\end{array}$

Rearrange for $v_x$:

$\begin{array}{l}6.8v_x=\left(2\text{A}\right)\left(20\text{Ω}\right)\\ 6.8v_x=40\text{V}\\ v_x=5.88\text{V}\end{array}$

The expression for the current flowing through $4\Omega$ resistor is as follows:

$i_R=\frac{v_x}{R_2}$ (10)

Here,

$i_R$ is the current flowing through $4\Omega$ resistor.

Substitute $5.88\text{V}$ for $v_x$ and $4\text{Ω}$ for $R_2$ in equation (10),

$\begin{array}{c}{i}_R=\frac{5.88\text{V}}{4\text{Ω}}\\ =1.47\text{A}\end{array}$

So, the current flowing through $4\Omega$ resistor for $t=\infty$ is $1.47\text{A}$.

Substitute $1.47\text{A}$ for $i\left(\infty \right)$, and $0\text{A}$ for $i\left(0\right)$ and $220.6\mu \text{s}$ for $\tau$ in equation (7):

$\begin{array}{c}i\left(t\right)=1.47\text{A}+\left(0\text{A}-1.47\text{A}\right)e^{-\frac{t}{220.6\mu \text{s}}}\\ =1.47\text{A}-1.47\text{A}{e}^{-\frac{t}{220.6\mu \text{s}}}\text{A}\end{array}$

$i\left(t\right)=1.47\left(1-e^{-\frac{t}{220.6\mu \text{s}}}\right)\text{A}$ (11)

The expression for the voltage across the $4\Omega$ resistor is as follows:

$v_x=i\left(t\right)R_2$ (12)

Substitute $1.47\left(1-e^{-\frac{t}{220.6\mu \text{s}}}\right)\text{A}$ for $i\left(t\right)$ and $4\text{Ω}$ for $R_2$ in equation (12):

$\begin{array}{c}{v}_x=1.47\left(1-e^{-\frac{t}{220.6\mu \text{s}}}\right)\text{A}\left(4\Omega \right)\\ =5.88\left(1-e^{-\frac{t}{220.6\mu \text{s}}}\right)\text{V}\end{array}$

Conclusion:

Thus, the expression for the voltage $v_x$ valid for all $t$ is $5.88\left(1-e^{-\frac{t}{220.6\mu \text{s}}}\right)\text{V}$.

To determine

Plot the power dissipated in the $4\text{Ω}$ resistor over the range of six time constants.

Explanation of Solution

Given data:

The range of the time is six time constant.

Formula used:

The expression for the power dissipated in the $4\text{Ω}$ resistor is as follows:

$p=\frac{{\left(v_x\right)}^2}{R_2}$ (12)

Here,

$p$ is the power dissipated in the $4\text{Ω}$ resistor.

Calculation:

Substitute $5.88\left(1-e^{-\frac{t}{220.6\mu \text{s}}}\right)\text{V}$ for $v_x$ and $4\text{Ω}$ for $R_2$ in equation (12):

$p=\frac{{\left(5.88\left(1-e^{-\frac{t}{220.6\mu \text{s}}}\right)\text{V}\right)}^2}{4\text{Ω}}$ (13)

The time constant of the circuit is $220.6\mu \text{s}$ as calculated in sub-part (a).

The different value for the power dissipated in the $4\text{Ω}$ resistor over the range of six time constants is given in the Table 1 as follows:

$\begin{array}{l}\begin{array}{ccc}n& t=n\tau \left(\mu \text{s}\right)& p\left(\text{W}\right)\\ 0& 0& 0\\ 0.5& 110.3& 1.3382\\ 1& 220.6& 3.4537\\ 1.5& 330.9& 5.2166\\ 2& 441.2& 6.4623\\ 2.5& 551.5& 7.2818\\ 3& 661.8& 7.8043\\ 4& 882.4& 8.3298\\ 5& 1103& 8.5275\\ 6& 1323.6& 8.6008\\ 7& 1544.2& 8.6278\\ 8& 1764.8& 8.6378\\ 9& 1985.4& 8.6414\\ 10& 2206& 8.6428\\ 11& 2426.6& 8.6433\\ 12& 2647.2& 8.6434\end{array}\\ \text{Table}\text{1}\end{array}$

The graph for power dissipated in the $4\text{Ω}$ resistor over the range of six time constants is plotted in Figure 3 as follows:

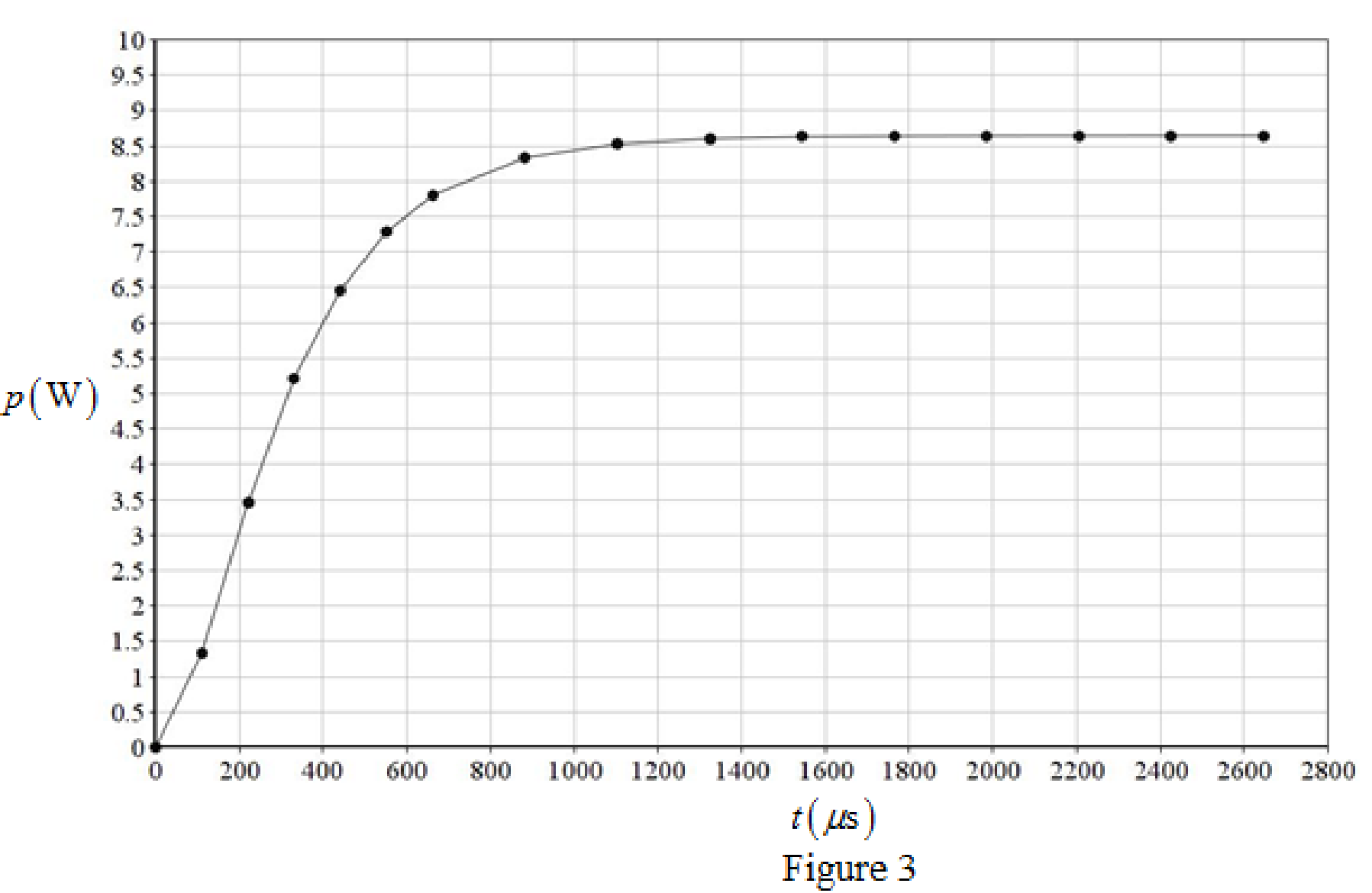
Calculation:

Thus, the graph for power dissipated in the $4\text{Ω}$ resistor over the range of six time constants is plotted in the Figure 3.

Conclusion:

To determine

Repeat parts (a) to (c) if the dependent source is installed in the circuit upside down.

Explanation of Solution

Calculation:

To find equivalent resistance of a circuit the independent current source is replaced by open circuit and $1\text{V}$ test source is connected across open circuit terminal.

The circuit diagram is redrawn as shown in Figure 4:

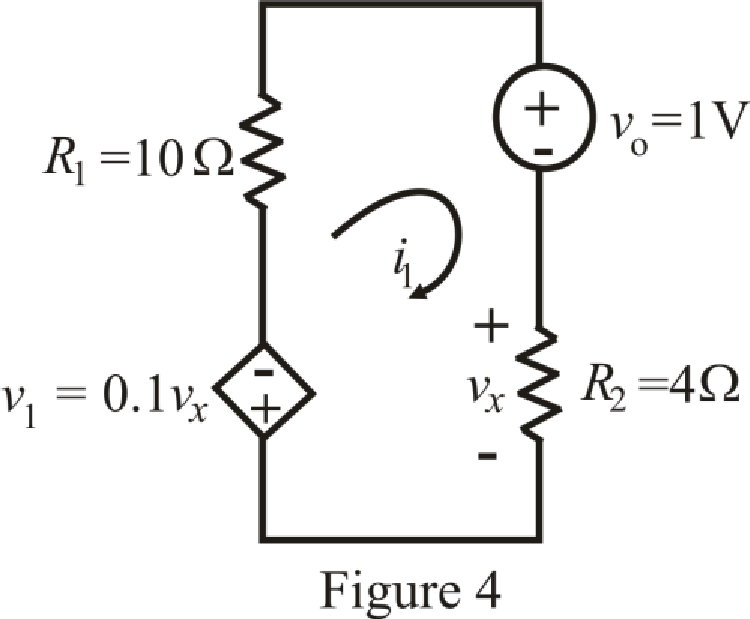
Refer to the redrawn Figure 4:

Apply KVL in mesh 1:

$v_1+i_1{R}_1+v_0+i_1{R}_2=0$ (14)

Here,

$v_1$ is the voltage of $0.1v_x$ dependent source,

$v_0$ are the voltage of $1\text{V}$ test source,

$i_1$ is the current flowing in mesh 1 and

$R_1$ is the resistance of $10\Omega$ resistor and

$R_2$ is the resistance of $4\Omega$ resistor.

Substitute $0.1v_x$ for $v_1$, $10\text{Ω}$ for $R_1$, $4\text{Ω}$ for $R_2$ and $1\text{V}$ for $v_0$ in equation (14):

$0.1v_x+\left(10\text{Ω}\right)i_1+1\text{V}+\left(4\text{Ω}\right)i_1=0$

$0.1v_x+14i_1+1\text{V}=0$ (15)

The expression for voltage across the $4\text{Ω}$ resistor is as follows:

$v_x=i_1{R}_2$ (16)

Here,

$v_x$ is voltage across resistor $4\text{Ω}$ resistor.

Substitute $4\text{Ω}$ for $R_2$ in equation (`16):

$v_x=i_1\left(4\text{Ω}\right)$

Substitute $i_1\left(4\text{Ω}\right)$ for $v_x$ in equation (15):

$\begin{array}{l}0.1\left(i_1\left(4\text{Ω}\right)\right)+14i_1+1\text{V}=0\\ 0.4i_1+14i_1+1\text{V}=0\end{array}$

$14.4i_1+1\text{V}=\text{0}$ (17)

Rearrange for $i_1$:

$\begin{array}{l}14.4i_1=-1\text{V}\\ i_1=\frac{-1}{14.4}\text{A}\\ =-0.0694\text{4}\text{A}\end{array}$

Substitute $1\text{V}$ for $v$ and $0.0694\text{4}\text{A}$ for $i$ in equation (1):

$\begin{array}{c}R=\frac{1\text{V}}{0.0694\text{4}\text{A}}\\ =14.4\text{Ω}\end{array}$

So, the equivalent resistance across inductor is $14.4\text{Ω}$.

Substitute $14.4\text{Ω}$ for $R_{eq}$ and $\text{3 mH}$ for $L$ in the equation (2):

$\begin{array}{c}\tau =\frac{\text{3 mH}}{14.4\text{Ω}}\\ =\frac{\text{3}}{14.4}\text{ms}\\ =0.2083\text{ms}\\ =208.3\mu \text{s}\left\{\because 1\text{ms}={10}^3\mu \text{s}\right\}\end{array}$

So, the time constant of the circuit is $208.3\mu \text{s}$.

The unit-step forcing function as a function of time which is zero for all values of its argument less than zero and which is unity for all positive values of its argument.

$u\left(t-t_0\right)=\{\begin{array}{l}0t<t_0\\ 1t>t_0\end{array}$

Here,

$t_0$ is the point at which the argument of unit step function becomes zero.

The independent voltage source is:

$i=2u\left(t\right)\text{ A}$ (18)

Substitute $0^{-}$ for $t$ in equation (18),

$\begin{array}{c}{i}_{0^{-}}=2u\left(0^{-}\right)\text{ A}\\ =2\left(0\right)\text{ A}\\ =\text{0}\text{A}\end{array}$

The current through $2u\left(t\right)\text{ A}$  independent current source is $0\text{A}$.

The $2u\left(t\right)\text{ A}$ independent current source behaves as open circuit and therefore no current flow in the circuit.

So, the value of the current flowing through the inductor for $t=0^{-}$ is $0\text{A}$.

The inductor does not allow sudden change in the current.

So,

$i\left(0^{+}\right)=i\left(0^{-}\right)$

Therefore, the current flowing in the circuit for $t=0$ is $0\text{A}$.

Substitute $\infty$ for $t$ in equation (18),

$\begin{array}{c}{i}_{\infty }=2u\left(\infty \right)\text{ A}\\ =2\left(1\right)\text{ A}\\ =2\text{A}\end{array}$

So, the current flowing through the $2u\left(t\right)\text{ A}$ independent current source for $t=\infty$ is $2\text{A}$.

The circuit diagram is redrawn as shown in Figure 5 for $t=\infty$.

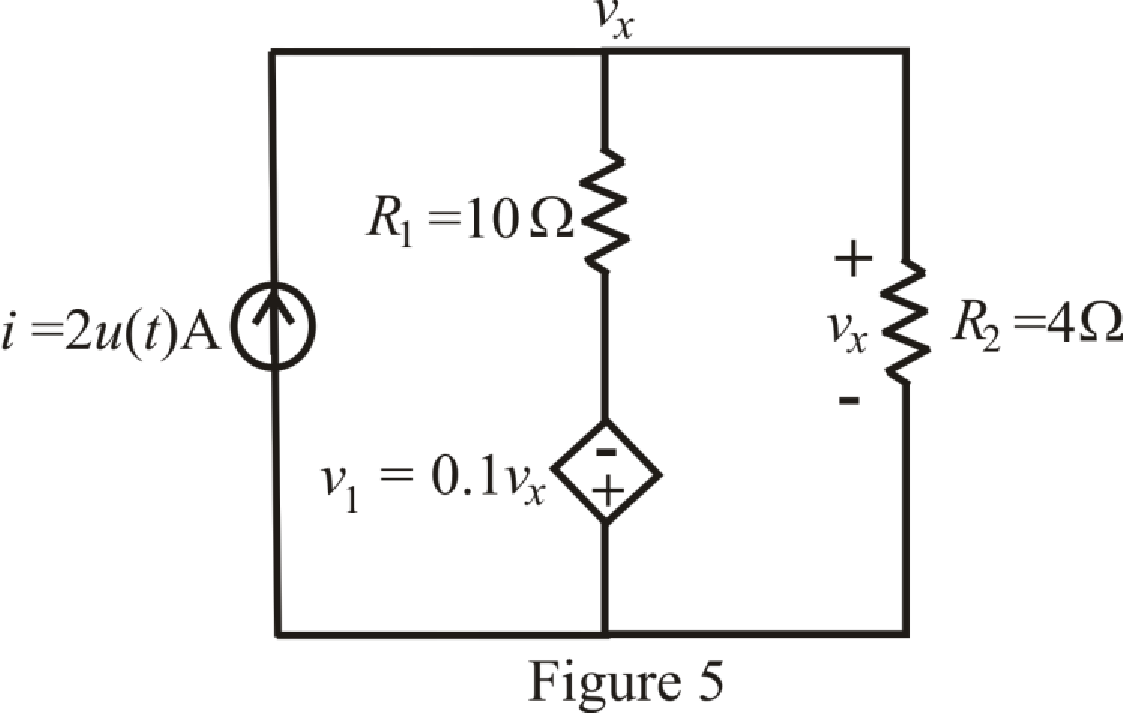
Refer to the redrawn Figure 5:

Apply KCL in the circuit:

$\frac{v_x+v_1}{R_1}+\frac{v_x}{R_2}=i$ (19)

Substitute $0.1v_x$ for $v_1$, $10\text{Ω}$ for $R_1$, $4\text{Ω}$ for $R_2$ and $2\text{A}$ for $i$ in equation (19):

$\begin{array}{l}\frac{v_x+0.1v_x}{10\text{Ω}}+\frac{v_x}{4\text{Ω}}=2\text{A}\\ \frac{2v_x+0.2v_x+5v_x}{20\text{Ω}}=2\text{A}\\ \frac{7.2v_x}{20\text{Ω}}=2\text{A}\end{array}$

Rearrange for $v_x$:

$\begin{array}{l}7.2v_x=\left(2\text{A}\right)\left(20\text{Ω}\right)\\ 7.2v_x=40\text{V}\\ v_x=5.56\text{V}\end{array}$

The expression for the current flowing through $4\Omega$ resistor is as follows:

$i_R=\frac{v_x}{R_2}$ (20)

Here,

$i_R$ is the current flowing through $4\Omega$ resistor.

Substitute $5.56\text{V}$ for $v_x$ and $4\text{Ω}$ for $R_2$ in equation (20):

So, the current flowing through $4\Omega$ resistor for $t=\infty$ is $1.389\text{A}$.

Substitute $1.389\text{A}$ for $i\left(\infty \right)$, and $0\text{A}$ for $i\left(0\right)$ and $208.3\mu \text{s}$ for $\tau$ in equation (7):

$\begin{array}{c}i\left(t\right)=1.389\text{A}+\left(0\text{A}-1.389\text{A}\right)e^{-\frac{t}{208.3\mu \text{s}}}\\ =1.389\text{A}-1.389\text{A}{e}^{-\frac{t}{208.3\mu \text{s}}}\text{A}\end{array}$

$i\left(t\right)=1.389\left(1-e^{-\frac{t}{208.3\mu \text{s}}}\right)\text{A}$ (21)

The expression for the voltage across the $4\Omega$ resistor is as follows:

$v_x=i\left(t\right)R_2$ (22)

Substitute $1.389\left(1-e^{-\frac{t}{208.3\mu \text{s}}}\right)\text{A}$ for $i\left(t\right)$ and $4\text{Ω}$ for $R_2$ in equation (22):

$\begin{array}{c}{v}_x=\left(1.389\left(1-e^{-\frac{t}{208.3\mu \text{s}}}\right)\text{A}\right)\left(4\Omega \right)\\ =5.56\left(1-e^{-\frac{t}{208.3\mu \text{s}}}\right)\text{V}\end{array}$

So, the expression for the voltage $v_x$ valid for all $t$ is $5.56\left(1-e^{-\frac{t}{208.3\mu \text{s}}}\right)\text{V}$.

Substitute $5.56\left(1-e^{-\frac{t}{208.3\mu \text{s}}}\right)\text{V}$ for $v_x$ and $4\text{Ω}$ for $R_2$ in equation (12):

$p=\frac{{\left(5.56\left(1-e^{-\frac{t}{208.3\mu \text{s}}}\right)\text{V}\right)}^2}{4\text{Ω}}$ (23)

The time constant of the circuit is $208.3\mu \text{s}$.

The different value for the power dissipated in the $4\text{Ω}$ resistor over the range of six time constants is given in the Table 2 as follows:

$\begin{array}{l}\begin{array}{ccc}n& t=n\tau \left(\mu \text{s}\right)& p\left(\text{W}\right)\\ 0& 0& 0\\ 0.5& 104.15& 1.1965\\ 1& 208.3& 3.0881\\ 1.5& 312.45& 4.6643\\ 2& 416.6& 5.7781\\ 2.5& 520.75& 6.5117\\ 3& 624.9& 6.9780\\ 4& 833.2& 7.4479\\ 5& 1041.5& 7.6246\\ 6& 1249.8& 7.6901\\ 7& 1458.1& 7.7143\\ 8& 1666.4& 7.7232\\ 9& 1874.7& 7.7264\\ 10& 2083& 7.7277\\ 11& 2291.3& 7.7281\\ 12& 2499.6& 7.7283\end{array}\\ \text{Table}2\end{array}$

The graph for power dissipated in the $4\text{Ω}$ resistor over the range of six time constants is plotted in Figure 6 as follows:

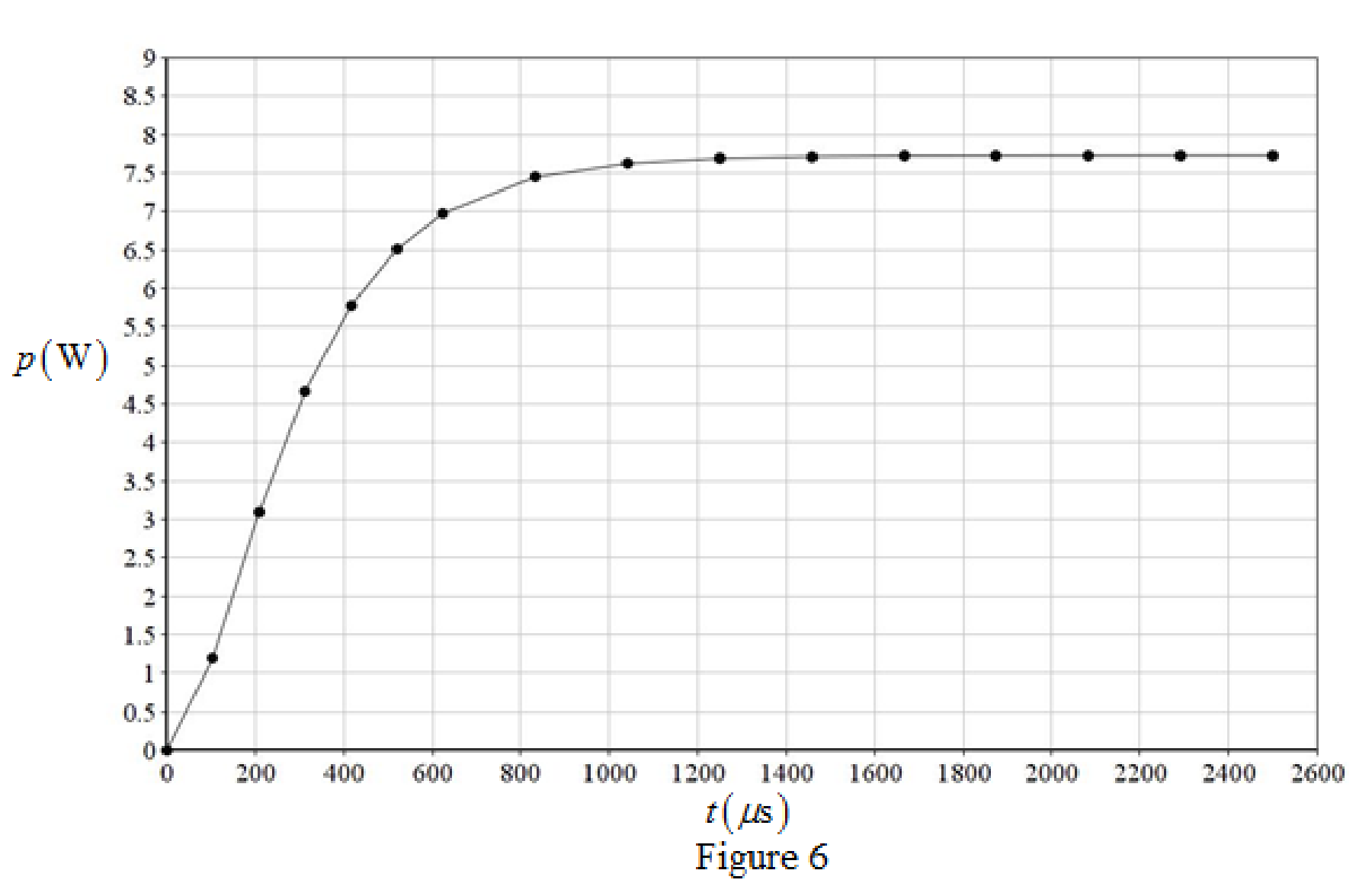
Conclusion:

Thus, the time constant of the circuit is $208.3\mu \text{s}$, the expression for the voltage $v_x$ valid for all $t$ is $5.56\left(1-e^{-\frac{t}{208.3\mu \text{s}}}\right)\text{V}$ and the graph for power dissipated in the $4\text{Ω}$ resistor over the range of six time constants is plotted in the Figure 6.

To determine

Are both circuit configurations “stable”? Explain.

Answer to Problem 76E

Both circuit configurations are “stable”.

Explanation of Solution

Refer to Figure 3 and Figure 6:

The response (output power dissipated in the $4\text{Ω}$ resistor) of both circuit approaches a steady state value at $t>0$.

So, both circuit configurations “stable”.

Conclusion:

Thus, both circuit configurations are “stable”.