
Concept explainers
(a)
Find the value of
(a)
Answer to Problem 28E
At
Explanation of Solution
Formula used:
The expression for the current flowing through the resistor is as follows.
Here,
Calculation:
The redrawn circuit diagram is given in Figure 1.
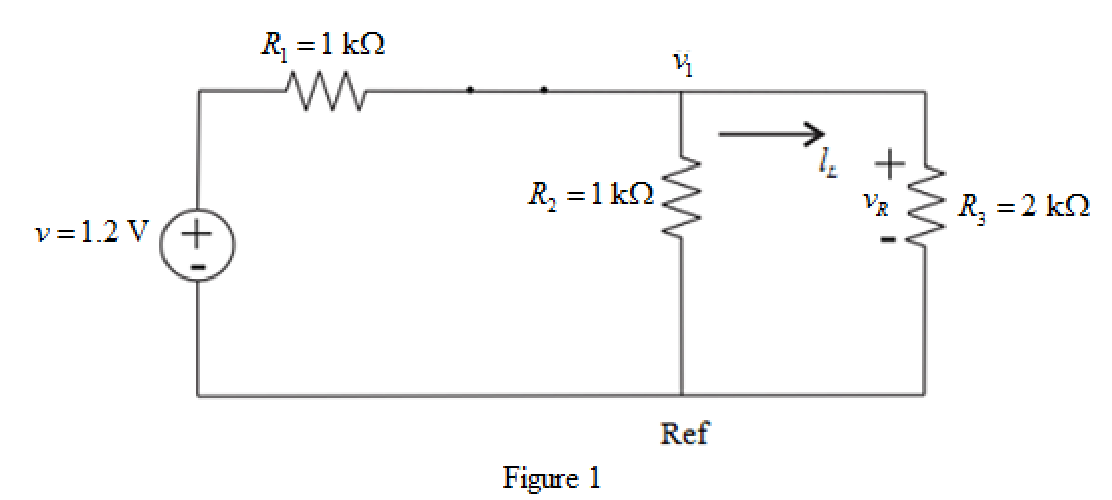
Refer to the redrawn Figure 1.
The given circuit inductor is connected for 6 years prior to being flipped open at
Apply KCL at node 1.
Here,
Substitute
Rearrange the above equation for
The voltage across
Substitute
Conclusion:
Thus, at
(b)
Find the value of
(b)
Answer to Problem 28E
At
Explanation of Solution
Calculation:
The redrawn circuit diagram is given in Figure 2.
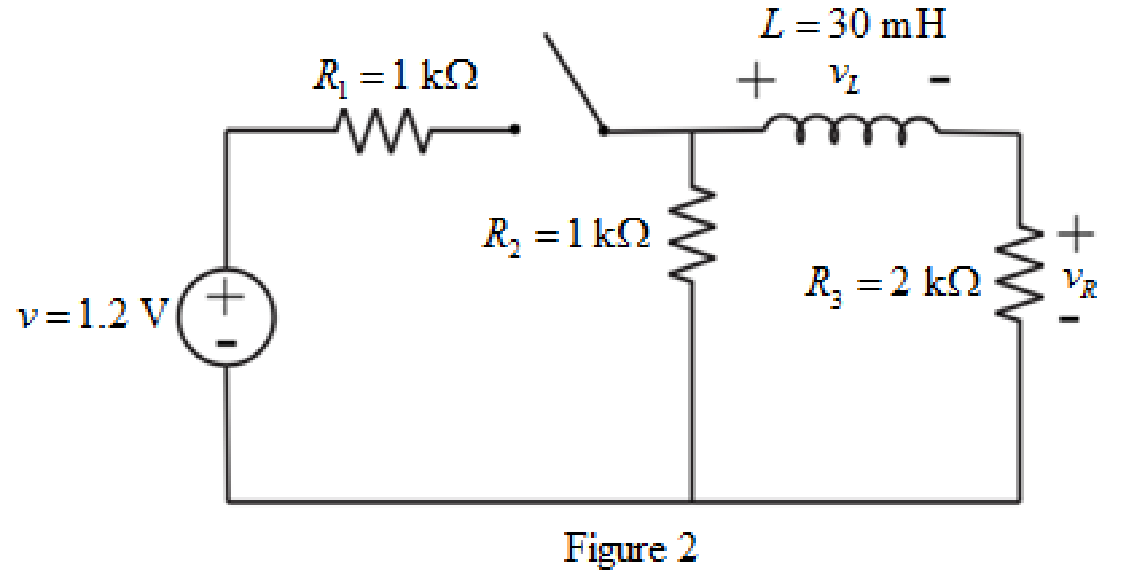
Refer to the redrawn Figure 2.
The expression for the voltage across the
Here,
Refer to the redrawn Figure 2.
The inductor does not allow sudden change in the current.
So, the current through inductor at
Apply KVL in the right side mesh.
Here,
Substitute
Rearrange for
Substitute
Conclusion:
Thus, at
(c)
Find the value of
(c)
Answer to Problem 28E
At
Explanation of Solution
Given data:
The time is
Formula used:
The expression for the equivalent resistor connected in series is as follows.
Here,
The expression for the time constant for
Here,
The expression for the current for
Here,
Calculation:
The redrawn circuit diagram is given in Figure 3.
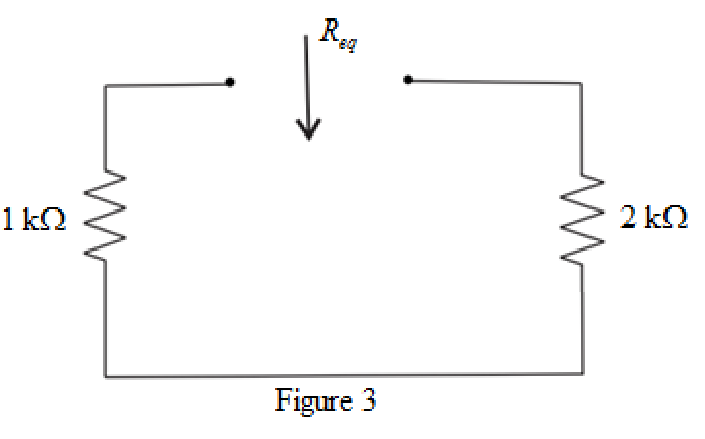
Refer to the redrawn Figure 3.
The simplified diagram is shown in Figure 4.
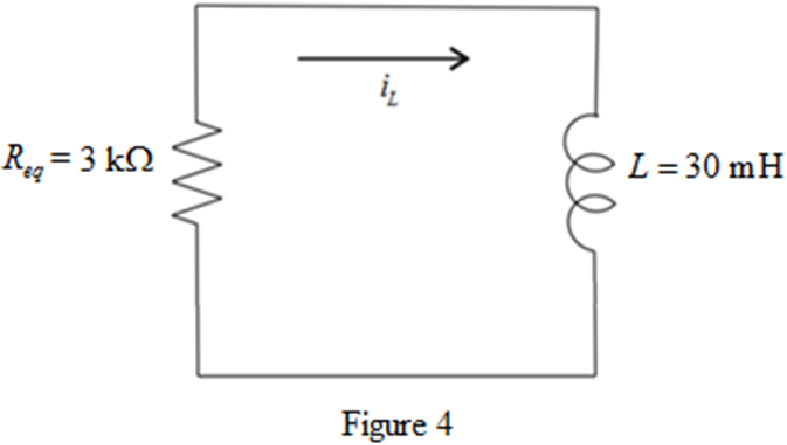
Refer to the redrawn Figure 4.
Substitute
Substitute
Substitute
Rearrange the above equation for
Substitute
Conclusion:
Thus, at
(d)
Find the value of
(d)
Answer to Problem 28E
At
Explanation of Solution
Given Data:
The time is
Calculation:
Substitute
Substitute
Rearrange the above equation for
Substitute
Conclusion:
Thus, at
Want to see more full solutions like this?
Chapter 8 Solutions
ENGINEERING CIRCUIT...(LL)>CUSTOM PKG.<
- An open-circuit voltage of 240 V appears across the slip-rings of a wound-rotor in- duction motor when the rotor is locked. The stator has 6 poles and is excited by a 60 Hz source. If the rotor is driven by a variable-speed dc motor, calculate the open-circuit voltage and frequency across the slip-rings if the dc motor turns a. At 600 r/min, in the same direction as the rotating field b. At 900 r/min, in the same direction as the rotating field c. At 3600 r/min, opposite to the rotating fieldarrow_forwardIf we double the number of poles on the stator of an induction motor, will its syn- chronous speed also double? The rotor of an induction should never be locked while full voltage is being applied to the stator. Explain. Why does the rotor of an induction motor turn slower than the revolving field?arrow_forwarda. Calculate the synchronous speed of a 3-phase, 12-pole induction motor that is excited by a 60 Hz source. b. What is the nominal speed if the slip at full-load is 6 percent?arrow_forward
- A 3-phase, 75 hp, 440 V induction motor has a full-load efficiency of 91 percent and a power factor of 83 percent. Calculate the nominal current per phase.arrow_forwardPlease answer all the questions a) What is the minimum required transformer rating for each transformer in kVA? b) Find the voltage required at Bus 1. c) The loadcentre is to be powered by PV panels that have the same I-V curve (ISC = 120 A, VOC = 60 V). Identify the configuration that uses the minimum number of panels to provide enough power to Bus 1. You can assume that the inverter converts the power at 95% efficiency and requires V DC input to generate the same VRMS AC output.arrow_forwardWhat happens to the rotor speed and rotor current when the mechanical load on an in- duction motor increases? Would you recommend using a 50 hp in- duction motor to drive a 10 hp load? Explain. Give two advantages of a wound-rotor mo- tor over a squirrel-cage motor. Both the voltage and frequency induced in the rotor of an induction motor decrease as the rotor speeds up. Explain.arrow_forward
- Please provide explainations and detailed working. thank youarrow_forwardPlease provide explainations and detailed working. thank youarrow_forwardThe excitation of a three-phase synchronous motor connected in parallel with a load of 500 kW operating at 0-85 p.f. lagging is adjusted to improve the overall p.f. of the system to 0.95 lagging. If the mechanical load on the motor is 120 kW, calculate the kVA input to the synchronous motor and its p.f.?arrow_forward
- A domestic load of 2300 kW at 0.88 p.f lagging and a motors load of 3400 kW at 0.85 p.f lagging are supplied by two alternators operating in parallel. If one alternator is delivering a load of 3300 kW at 0.9 p.f lagging, what will be the output power and p.f of the other alternator?arrow_forwardDesign a bank of capacitors to provide 60V and 2kWh energy to capture and store regen breaking energy. Use commercial supercapacitor cells at 3V and 3600F. Capacitor voltage drops almost linearly during discharge and below half voltage maximum it doesn’t provide significant power. If we discharge a fully charged capacitor to its half voltage maximum, how much energy can be discharged compared to a full-discharged capacitor (show your calculation)?arrow_forward8-1) similar to Lathi & Ding, Prob. P.5.1-2 The figure below shows the Fourier spectra of signals of g,(t) and g₁(t). Determine the Nyquist rate and the corresponding sampling interval for signals of g,(t), g,(t), g₁(1) - g¸(1), g¸³(t), and g₁(1)g₁(1). Hint: Use the frequency convolution and the width property of convolution. G₁(f) G₂(f) -8000 0 8000 f -20000 10 20000 farrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





