
Concept explainers
(a)
To find area of region R
(a)
Answer to Problem 53RE
Area of Region R
Explanation of Solution
Given:
Region R in the first quadrant enclosed by the y-axis and the graphs of
Concept Used:
Area between the curves
Given region R is in the first quadrant by the y-axis and the graphs of
Getting limits by solving using graphing calculator
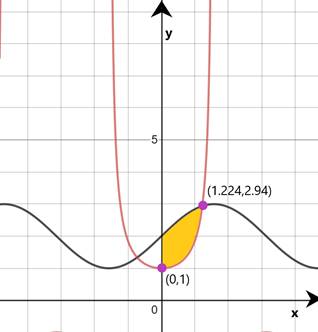
Therefore,
Limits are
Calculation:
Area of region R,
Conclusion:
Area of Region R
(b)
To find the volume of the solid generated when region R is revolved about
(b)
Answer to Problem 53RE
Volume of the solid generated when region R is revolved about
Explanation of Solution
Given:
Region R in the first quadrant enclosed by the y-axis and the graphs of
Concept Used:
The volume V of a solid generated by revolving the region about
Calculation:
Now finding definite integral,
Conclusion:
Required Volume, V=
c.
To find volume of the solid whose base is region R and whose cross sections cut by planes perpendicular to
c.
Answer to Problem 53RE
Volume of the solid whose base is region R and whose cross sections cut by planes perpendicular to
Explanation of Solution
Given:
The solid whose base is region R and whose cross sections cut by planes perpendicular to
Concept Used:
Volume of the solid whose base is region R and whose cross sections cut by planes perpendicular to
Calculation:
Now finding definite integral by putting values of limits
Conclusion:
Required Volume
Chapter 8 Solutions
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)
Additional Math Textbook Solutions
Basic Business Statistics, Student Value Edition
College Algebra with Modeling & Visualization (5th Edition)
Algebra and Trigonometry (6th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Introductory Statistics
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
- Determine the values and locations of the global (absolute) and local extrema on the graph given. Assume the domain is a closed interval and the graph represents the entirety of the function. 3 y -6-5-4-3 2 1 -1 -2 -3 Separate multiple answers with a comma. Global maximum: y Global minimum: y Local maxima: y Local minima: y x 6 at a at a at x= at x=arrow_forwardA ball is thrown into the air and its height (in meters) is given by h (t) in seconds. -4.92 + 30t+1, where t is a. After how long does the ball reach its maximum height? Round to 2 decimal places. seconds b. What is the maximum height of the ball? Round to 2 decimal places. metersarrow_forwardDetermine where the absolute and local extrema occur on the graph given. Assume the domain is a closed interval and the graph represents the entirety of the function. 1.5 y 1 0.5 -3 -2 -0.5 -1 -1.5 Separate multiple answers with a comma. Absolute maximum at Absolute minimum at Local maxima at Local minima at a x 2 3 аarrow_forward
- A company that produces cell phones has a cost function of C = x² - 1000x + 36100, where C is the cost in dollars and x is the number of cell phones produced (in thousands). How many units of cell phones (in thousands) minimizes this cost function? Round to the nearest whole number, if necessary. thousandarrow_forwardUnder certain conditions, the number of diseased cells N(t) at time t increases at a rate N'(t) = Aekt, where A is the rate of increase at time 0 (in cells per day) and k is a constant. (a) Suppose A = 60, and at 3 days, the cells are growing at a rate of 180 per day. Find a formula for the number of cells after t days, given that 200 cells are present at t = 0. (b) Use your answer from part (a) to find the number of cells present after 8 days. (a) Find a formula for the number of cells, N(t), after t days. N(t) = (Round any numbers in exponents to five decimal places. Round all other numbers to the nearest tenth.)arrow_forwardThe marginal revenue (in thousands of dollars) from the sale of x handheld gaming devices is given by the following function. R'(x) = 4x (x² +26,000) 2 3 (a) Find the total revenue function if the revenue from 125 devices is $17,939. (b) How many devices must be sold for a revenue of at least $50,000? (a) The total revenue function is R(x) = (Round to the nearest integer as needed.) given that the revenue from 125 devices is $17,939.arrow_forward
- Use substitution to find the indefinite integral. S 2u √u-4 -du Describe the most appropriate substitution case and the values of u and du. Select the correct choice below and fill in the answer boxes within your choice. A. Substitute u for the quantity in the numerator. Let v = , so that dv = ( ) du. B. Substitute u for the quantity under the root. Let v = u-4, so that dv = (1) du. C. Substitute u for the quantity in the denominator. Let v = Use the substitution to evaluate the integral. so that dv= ' ( du. 2u -du= √√u-4arrow_forwardUse substitution to find the indefinite integral. Зи u-8 du Describe the most appropriate substitution case and the values of u and du. Select the correct choice below and fill in the answer boxes within your choice. A. Substitute u for the quantity in the numerator. Let v = , so that dv = ( ( ) du. B. Substitute u for the quantity under the root. Let v = u-8, so that dv = (1) du. C. Substitute u for the quantity in the denominator. Let v = so that dv= ( ) du. Use the substitution to evaluate the integral. S Зи -du= u-8arrow_forwardFind the derivative of the function. 5 1 6 p(x) = -24x 5 +15xarrow_forward
- ∞ 2n (4n)! Let R be the radius of convergence of the series -x2n. Then the value of (3" (2n)!)² n=1 sin(2R+4/R) is -0.892 0.075 0.732 -0.812 -0.519 -0.107 -0.564 0.588arrow_forwardFind the cost function if the marginal cost function is given by C'(x) = x C(x) = 2/5 + 5 and 32 units cost $261.arrow_forwardFind the cost function if the marginal cost function is C'(x) = 3x-4 and the fixed cost is $9. C(x) = ☐arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





