Chapter 7.1, Problem 38E

To determine

To match the slope $\frac{dy}{dx}=y-x$ with the correct graph and to find the particular solution for the point $\left(3,2\right)$ .

Answer to Problem 38E

The correct graph of the given slope $\frac{dy}{dx}=y-x$ is,

  

The graph of the point (3,2) on the given slope is,

  

Explanation of Solution

Given information :

The slope $\frac{dy}{dx}=y-x$ .

Calculation:

Consider, the slope $\frac{dy}{dx}=y-x$ .

Using the above value it is clear that, when $x=y$ then the slope become $\frac{dy}{dx}=x-x=0$ .

Hence the slope can only be zero when $x=y$ .

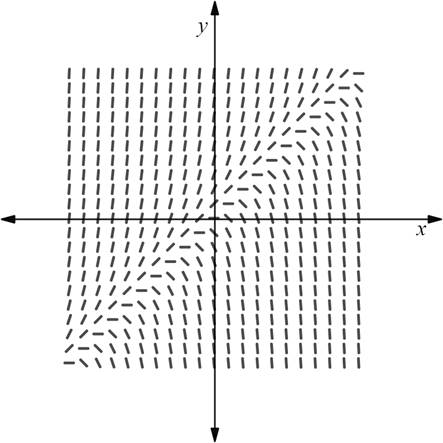
Thus, the graphs B and E can be eliminated since they have slopes of zero at all the points on x -axis.

Also, the graph s of C and F can be eliminated since they have slopes of zero at all the points of y -axis.

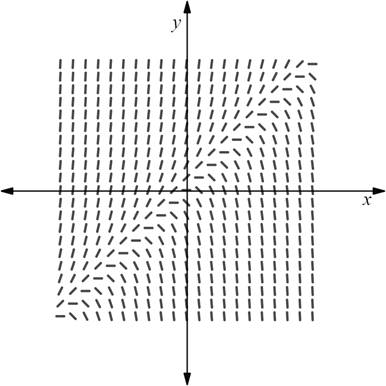
Therefore, the graph of A or D is the match for the slope $\frac{dy}{dx}=y-x$ .

Consider the point $\left(3,2\right)$ substitute it in the slope $\frac{dy}{dx}=y-x$ ,

  $\Rightarrow \frac{dy}{dx}=2-3=-1$

(i.e.,) The slope is negative at the point $\left(3,2\right)$ . But on the graph of Ahave positive slope at the point $\left(3,2\right)$ .

Hence, the graph of the slope field is in the form,

  

Thus, from the given set of graphs option D is the correct match for the slope $\frac{dy}{dx}=y-x$ .

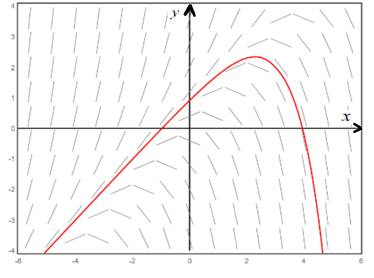
Now, to find the particular solution through the above graph for the point $\left(3,2\right)$ .

Consider the point $\left(3,2\right)$ by using the line segment at the point $x=2$ sketch the additional portion of the curve to have the slope and similarly using the line segment at the point $x=3$ again sketch the curve continuing the similar process to fill the entire sketch then the final curve results as,

  

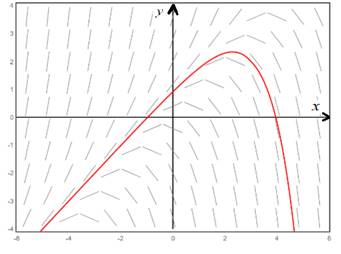
Which is the particular solution for the slope $\frac{dy}{dx}=y-x$ at the point $\left(3,2\right)$ .