
For the potentiometer in Fig. 7.95:
a. What are the voltages Vab and Vbc with no load applied
b. What are the voltages
c. What is the power dissipated by the potentiometer under the loaded conditions in Fig. 7.95?
d. What is the power dissipated by the potentiometer with no loads applied? Compare it to the results of part (c).
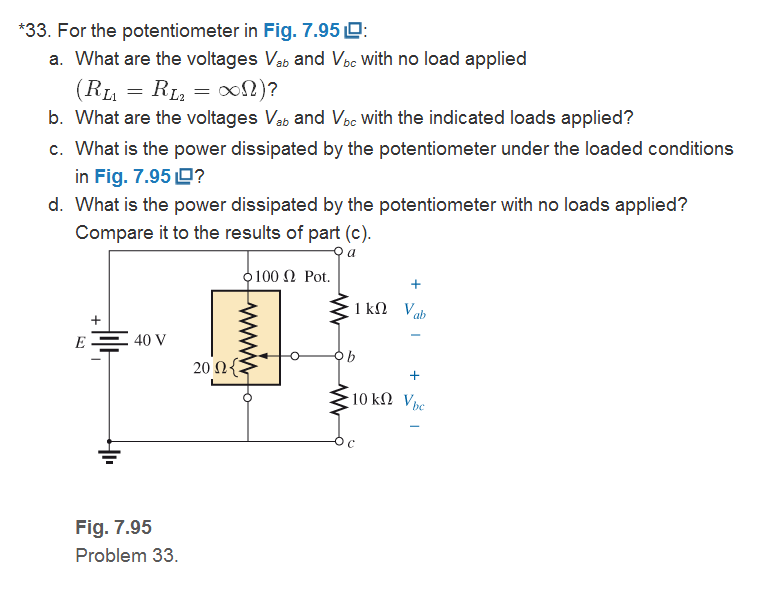
Fig. 7.95
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
Introductory Circuit Analysis (13th Edition)
Additional Engineering Textbook Solutions
Mechanics of Materials (10th Edition)
Electric Circuits. (11th Edition)
Modern Database Management
Automotive Technology: Principles, Diagnosis, And Service (6th Edition) (halderman Automotive Series)
Java: An Introduction to Problem Solving and Programming (8th Edition)
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
- NO AI PLEASE SHOW WORKarrow_forwardConsider a Continuous- time LTI System. described by y' (+)+ nycH) = x(+) find yet for усн b) x(+) = u(+) Sul. a) x(+)= ētu(+). c) X(+= √(+) jw few) +2 kW) = X (w) (jw+2) Y(W)= X(w) Han Youn X(w) ½ztjuk a) X (W) = 1 + jw Y(W)= X(w) H(W). I tjw z+jw tjw = 1+jw 2+jw y (+) = (e+ - e²+) 4(+) b) XIW): π (W) + |/|/w Y₁W) = [π √(W) + 1/w] =² + j w zxjw How = π √(w) 1 ㅠ беш) 24jw + *= II 8 (W) + 1 1 1 1 2 4 jw = 2 y(+)= \uct) - e²+us+] - SINAALINE ju 2+ jwarrow_forwardNO AI PLEASE SHOW WORKarrow_forward
- Don't use ai to answer I will report you answerarrow_forwardCompute the Laplace transform of the following time domain function using only L.T. properties: f(t)=(t-3)eu(t-2) The Laplace Transform of x(t) = 8(-1) - u(1) is X(s): = (a) 2πδ(s) (b) 1-1 S (c) j2πδ (s) (d) - 1/3 Sarrow_forwardUf you don't know, don't attempt this questions,no Ai or it's screen shot should be usedarrow_forward
- Find the initial and final values of sequence x(n) from X(Z) below using the initial and final value properties X(Z) = = z-1arrow_forwardOnly expert should attempt,no Ai or screen shot it solving, I need solution s to all of themarrow_forwardDon't use ai to answer I will report you answerarrow_forward
- Find the autocorrelation function of the periodic function x(t) 1 0 1 2 3 tarrow_forwardFind Laplace transform for x(t) = e−³t √∞ (1 − t) sin(t − 2) §(t)dt Find Laplace transform and the corresponding ROC for x(t) = e˜³τsin(2t) u(t)dtarrow_forwardfind the inverse Laplace transform of X(s)=- s+5 (s-1)(s-2)(s-3) i) Re[s]> 3 ii) Re[s]<1 iii) 1arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
