
Concept explainers
A Rotating Beacon Suppose that a fire truck is parked in front of a building as shown in the figure.
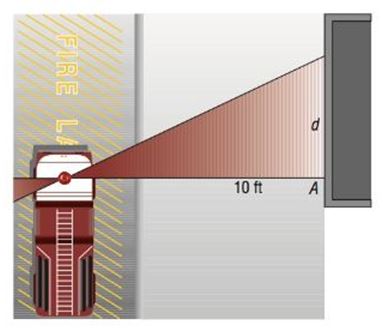
The beacon light on top of the fire truck is located 10 feet from the wall and has a light on each side. If the beacon light rotates 1 revolution every 2 seconds, then a model for determining the distance , in feet, that the beacon of light is from point A on the wall after seconds is given by
(a) Graph for .
(b) For what values of is the function undefined? Explain what this means in terms of the beam of light on the wall.
(c) Fill in the following table.

(d) Compute , and so on, for each consecutive value of . These are called first differences.
(e) Interpret the first differences found in part . What is happening to the speed of the beam of light as increases?
To find:
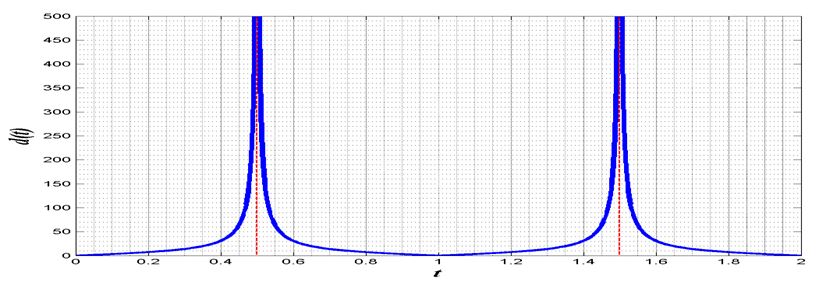
a. Graph for .
Answer to Problem 52AYU
Solution:
a.
Explanation of Solution
Given:
The function .
Calculation:
a. Graphing the given expression in either a graphing calculator, or using the method outlined in the solutions and using the vertical reflection operation needed to reflect the negative halves of the tangent into the positive side of the y-axis for the absolute value operation. We obtain the following graph.

To find:
b. For what values of t is the function undefined? Explain what this means in terms of the beam of light o the wall.
Answer to Problem 52AYU
Solution:
b.
Explanation of Solution
Given:
The function .
Calculation:
b. since , this function is undefined when for integer . in the interval provided the undefined values are going to be:
, from this list we choose the first two, since the third is outside the range given.
In terms of the light these times correspond to the times when the light beam is parallel to the wall, where it intersect the wall at infinity, which makes for either time point. Assuming the light is rotating counterclockwise in the figure given, and noting that for , which corresponds to time when the light is pointing straight at the wall at point , then corresponding to the time when the light is pointing directly in the front of truck parallel to the wall. Then one second after that (the time it takes that same beam to traverse the other half of the rotation)the beam is pointing directly behind the truck, parallel to the wall.
To find:
c. Fill in the following table.
Answer to Problem 52AYU
Solution:
c.
Explanation of Solution
Given:
The function .
Calculation:
c.
To find:
d. Compute and so on, for each consecutive value of .
Answer to Problem 52AYU
Solution:
d.
Explanation of Solution
Given:
The function .
Calculation:
d.
To find:
e. Interpret the first differences found in part d. What is happening to the speed of the beam of light as increases?
Answer to Problem 52AYU
Solution:
e. The results in part d are like an approximation to the velocity of the light beam along width of the wall. We see that as the beam travels further away from point , the of the beam increases, and is in fact nonlinear in its variation (since for equal increments in time the differences in these first differences is not uniform). In fact as we approach the point where the light detaches from the wall at infinity the velocity increases all the way to infinity, as told by the converging upon the vertical line of the asymptote.
Explanation of Solution
Given:
The function .
Calculation:
e. The results in part d are like an approximation to the velocity of the light beam along width of the wall. We see that as the beam travels further away from point , the of the beam increases, and is in fact nonlinear in its variation (since for equal increments in time the differences in these first differences is not uniform). In fact as we approach the point where the light detaches from the wall at infinity the velocity increases all the way to infinity, as told by the converging upon the vertical line of the asymptote.
Chapter 6 Solutions
Precalculus Enhanced with Graphing Utilities
Additional Math Textbook Solutions
College Algebra (7th Edition)
Pre-Algebra Student Edition
Algebra and Trigonometry (6th Edition)
Thinking Mathematically (6th Edition)
University Calculus: Early Transcendentals (4th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
- 3 Evaluate the double integral 10 y√x dy dx. First sketch the area of the integral involved, then carry out the integral in both ways, first over x and next over y, and vice versa.arrow_forwardQuestion 2. i. Suppose that the random variable X takes two possible values 1 and -1, and P(X = 1) = P(X-1)=1/2. Let Y=-X. Are X and Y the same random variable? Do X and Y have the same distribution? Explain your answer. ii. Suppose that the random variable X~N(0, 1), let Y=-X. Are X and Y the same random variable? Do X and Y have the same distribution? Explain your answer.arrow_forwardProblem 4. Let f(x, y) = { Find P(X <1/2|Y = 1/2). c(x + y²) 0arrow_forwardAccording to Newton's law of universal gravitation, the force F between two bodies of constant mass GmM m and M is given by the formula F = , where G is the gravitational constant and d is the d² distance between the bodies. a. Suppose that G, m, and M are constants. Find the rate of change of force F with respect to distance d. F' (d) 2GmM b. Find the rate of change of force F with gravitational constant G = 6.67 × 10-¹¹ Nm²/kg², on two bodies 5 meters apart, each with a mass of 250 kilograms. Answer in scientific notation, rounding to 2 decimal places. -6.67x10 N/m syntax incomplete.arrow_forwardSolve please and thank youarrow_forwardmv2 The centripetal force of an object of mass m is given by F (r) = rotation and r is the distance from the center of rotation. ' where v is the speed of r a. Find the rate of change of centripetal force with respect to the distance from the center of rotation. F(r) b. Find the rate of change of centripetal force of an object with mass 500 kilograms, velocity of 13.86 m/s, and a distance from the center of rotation of 300 meters. Round to 2 decimal places. N/m (or kg/s²) F' (300)arrow_forwardSolve work shown please and thanks!arrow_forwardGiven the following graph of the function y = f(x) and n = = 6, answer the following questions about the area under the curve from x graph to enlarge it.) 1 (Round your answer to within two decimal places if necessary, but do not round until your final computation.) a. Use the Trapezoidal Rule to estimate the area. Estimate: T6 G b. Use Simpson's Rule to estimate the area. Estimate: S6 - ID = 0 to x = 6. (Click on aarrow_forward"Solve the following differential equation using the Operator Method and the Determinant Method:" Solve by dr no ai """'+3y"" + 3y+y=arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





