
To find: Explain how the amplitude and period of a sinusoidal graph are used to establish the scale on each coordinate axis:
Answer to Problem 39AYU
Solution:
Sinusoidal functions produce graphs that look like waves, and any portion of the curve can be translated onto another portion of the curve. Circular motion and pendulum movement are excellent “real life” examples of sinusoidal relationships.
A sinusoidal function is a function that is like a function in the sense that the function can be produced by shifting, stretching or compressing the function.
You can graph sinusoidal functions using your knowledge of transformations.
There are 5 transformations that can affect trig functions:
- horizontal stretch (HS) alters the period
- vertical stretch (VS) alters the amplitude
- horizontal translation (HT) causes a phase shift relocating our initial point
- vertical translation (VT) relocates the sinusoidal axis
- reflection (± )changes the pattern of our 5 key points
Explanation of Solution
Sinusoidal functions produce graphs that look like waves, and any portion of the curve can be translated onto another portion of the curve. Circular motion and pendulum movement are excellent “real life” examples of sinusoidal relationships.
A sinusoidal function is a function that is like a function in the sense that the function can be produced by shifting, stretching or compressing the function.
You can graph sinusoidal functions using your knowledge of transformations.
There are 5 transformations that can affect trig functions:
- horizontal stretch (HS) alters the period
- vertical stretch (VS) alters the amplitude
- horizontal translation (HT) causes a phase shift relocating our initial point
- vertical translation (VT) relocates the sinusoidal axis
- reflection (± )changes the pattern of our 5 key points
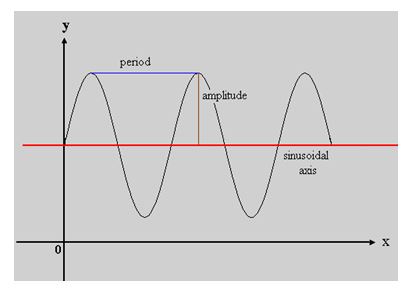
Some basic vocabulary should be observed as shown in the diagram:
Period: a complete cycle of the graph where the graph starts to repeat.
Sinusoidal axis: horizontal line halfway between the
Amplitude: vertical distance from the sinusoidal axis to the maximum or minimum
Local maximum: the tops of each “wave”, all equal in value
The relations involving or can be expressed in the form:
- Determine the position of the sinusoidal axis.
This is the Vertical Translation or “D” in the formula.
- Determine the amplitude of the function.
This is the Vertical Stretch or “A” in the formula.
- Determine the period of the graph for the function.
This is the Horizontal Stretch or “B” in the formula.
- Determine the phase shift.
This is the Horizontal Translation or “C” in the formula.
Graphing a Sinusoidal Function
The procedure for graphing sinusoidal functions is similar to quadratic functions.
or
Here A is the amplitude function. We know the maximum and minimum value of and is . Therefore takes value from to .
Both and have the domain is .
Therefore takes values are .
Chapter 6 Solutions
Precalculus Enhanced with Graphing Utilities
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
Elementary Statistics
Introductory Statistics
Algebra and Trigonometry (6th Edition)
Elementary Statistics (13th Edition)
College Algebra (7th Edition)
- (2) (22 points) Let F(x, y, z) = (x sin y, cos y, ―xy). (a) (2 points) Calculate V. F. (b) (6 points) Given a vector field is everywhere defined with V G₁(x, y, z) = * G2(x, y, z) = − G3(x, y, z) = 0. 0 0 F(x, y, z) = (F₁(x, y, z), F₂(x, y, z), F(x, y, z)) that F = 0, let G = (G1, G2, G3) where F₂(x, y, y, t) dt - √ F³(x, t, 0) dt, * F1(x, y, t) dt, t) dt - √ F Calculate G for the vector field F(x, y, z) = (x sin y, cos y, -xy).arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √(x + y) A R R = {(x, y) | 25 < x² + y² ≤ 36, x < 0} Hint: The integral and Region is defined in rectangular coordinates.arrow_forwardFind the volume of the solid that lies under the paraboloid z = 81 - x² - y² and within the cylinder (x − 1)² + y² = 1. A plot of an example of a similar solid is shown below. (Answer accurate to 2 decimal places). Volume using Double Integral Paraboloid & Cylinder -3 Hint: The integral and region is defined in polar coordinates.arrow_forward
- Evaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √4(1–2² 4(1 - x² - y²) dA R 3 R = {(r,0) | 0 ≤ r≤ 2,0π ≤0≤¼˜}. Hint: The integral is defined in rectangular coordinates. The Region is defined in polar coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). R - 1 · {(r,0) | 1 ≤ r≤ 5,½π≤ 0<1π}. Hint: Be sure to convert to Polar coordinates. Use the correct differential for Polar Coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √2(x+y) dA R R = {(x, y) | 4 < x² + y² < 25,0 < x} Hint: The integral and Region is defined in rectangular coordinates.arrow_forward
- HW: The frame shown in the figure is pinned at A and C. Use moment distribution method, with and without modifications, to draw NFD, SFD, and BMD. B I I 40 kN/m A 3 m 4 marrow_forwardLet the region R be the area enclosed by the function f(x)= = 3x² and g(x) = 4x. If the region R is the base of a solid such that each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in the region R, find the volume of the solid. You may use a calculator and round to the nearest thousandth. y 11 10 9 00 8 7 9 5 4 3 2 1 -1 -1 x 1 2arrow_forwardLet the region R be the area enclosed by the function f(x) = ex — 1, the horizontal line y = -4 and the vertical lines x = 0 and x = 3. Find the volume of the solid generated when the region R is revolved about the line y = -4. You may use a calculator and round to the nearest thousandth. 20 15 10 5 y I I I | I + -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 -5 I -10 -15 I + I I T I I + -20 I + -25 I I I -30 I 3.5 4 xarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





