Chapter 6.5, Problem 51AYU

Carrying a Ladder around a Corner Two hallways, one of width 3 feet, the other of width 4 feet, meet at a right angle. See the illustration.

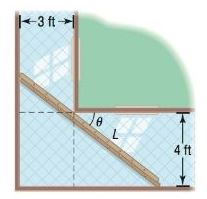
(a) Show that the length $L$ of the ladder shown as a function of the angle $\theta$ is

$L\left(\theta \right)=3\sec \theta +4\csc \theta$

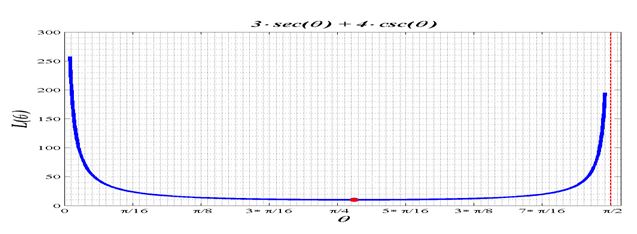
(b) Graph $L=L\left(\theta \right),\text{0}\text{<}\theta \text{<}\frac{\pi }{2}$

(c) For what value of $\theta$ is $L$ the least?

(d) What is the length of the longest ladder that can be carried around the corner? Why is this also the least value of $L$?

To determine

To find:

a. show that the length $L$ of the ladder shown as a function of the angle $\theta$ is $L\left(\theta \right)=3\sec \theta +4\cos \theta$.

Answer to Problem 51AYU

Solution:

a. $L\left(\theta \right)=3\sec \theta +4\cos \theta$

Explanation of Solution

Given:

The function $L\left(\theta \right)=3\sec \theta +4\cos \theta$.

Calculation:

a. To solve this we divide up the length $L$ into two segments, the portion lying in the 3 foot hallway, and the other portion lying in the 4 foot hallway. Call these lengths $L_3$ and $L_4$ respectively. We can consider these lengths as the radius radiating from the inner corner point of the walkway, where $\theta$ is measured from. Therefore from the labeled angle $\theta$, and its vertical angle equivalent on the opposite side(using the horizontal dotted line running through the 3 foot hallway), we see that:

$\cos \theta =\frac{3}{L_3}\Rightarrow L_3=\frac{3}{\cos \theta }=3\sec \theta$, $\sin \theta =\frac{4}{L_4}\Rightarrow L_4=\frac{4}{\sin \theta }=4\cos \theta$. Since the ladder is conceptually divided into two parts, we must have $L=L_3+L_4=3\sec \theta +4\cos \theta =L\left(\theta \right)$.

To determine

To find:

b. Graph $L=L\left(\theta \right),0<\theta <\frac{\pi }{2}$.

Answer to Problem 51AYU

Solution:

b. graph.

Explanation of Solution

Given:

The function $L\left(\theta \right)=3\sec \theta +4\cos \theta$.

Calculation:

b. Noting how the interval provided is an open interval(due to the undefined nature of the terms at those end points) we must in reality graph the function along a close but smaller interval, say $\frac{1}{100}.\frac{\pi }{2}<\theta <\frac{\pi }{2}.\frac{1}{100}.\frac{\pi }{2}-\Rightarrow \frac{\pi }{100}<\theta <\frac{99\pi }{100}$. Doing so gives us the following graph.

To determine

To find:

c. For what value of $\theta$ is $L$ the least?

Answer to Problem 51AYU

Solution:

c. $\theta \approx 0.83$

Explanation of Solution

Given:

The function $L\left(\theta \right)=3\sec \theta +4\cos \theta$.

Calculation:

c. From the above figure we can see a symmetric like bowl shape made by the curve for this interval. Being symmetric the curve decreases from the left and increases to the right, which appears to have a minimum right at the center of the interval $=\frac{\pi }{4}$. zooming in, doing a point trace, or using the fmin function in a calculator however will show that the minimum really occurs around $\theta \approx 0.8332718598$.

To determine

To find:

d. What is the length of the longest ladder that can be carried around the corner? Why is this also the least value of $L$?

Answer to Problem 51AYU

Solution:

d. $L({\theta }_c)\approx 9.86$

Explanation of Solution

Given:

The function $L\left(\theta \right)=3\sec \theta +4\cos \theta$.

Calculation:

d. Since the above equation uses the full ladder possible for each value $\theta$, essentially setting the halves of the ladder that span from the corner point to the full length possible for that radius(some angles even permitting lengths being infinitely long, assuming the hallways continue on forever)it can be seen that some lengths are too long, when coming from either $\theta =0$ or $\theta =\frac{\pi }{2}$. However when approaching them either of the two sides of being too long, towards the center of the interval we come to that point where being too long from either side meet one another. Consider the following thought experiment, say we take a given angle $\theta$, let the length span the fully allowed extent, then decrease it by some small amount. We could slide the ladder down to another angle $\theta \text{'}$ where the ladder makes a perfect full span fit. We could do this again and again, except for when we start at that minimal point where the length would become too small to fit the full span.

It is that point where the ladder can perfectly fit and be the longest it can be to be carried around the corner. In calculus class we can show that the angle theta that permits this is: ${\theta }_c={\tan }^{-1}\left[{\left(\frac{4}{3}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right]\approx 0.8332718598$.

And the corresponding ladder length is $L({\theta }_c)\approx 9.865662555$.