Chapter 6.4, Problem 7E

Interpretation Introduction

Interpretation:

Determine the stability of the fixed point at the origin and find is there any other fixed points for the system. Depending on other parameters sketch the qualitatively different types of phase portrait.

Concept Introduction:

The parametric curves traced by solutions of a differential equation are known as trajectories.

The geometrical representation of collection of trajectories in a phase plane is called as phase portrait.

The point which satisfies the condition ${\text{f(x}}^{\text{*}}\text{)=0}$ is known as fixed point, it correspond to steady state of the system (or equilibria of the system).

Closed Orbit corresponds to periodic solution of the system i.e. $\text{x(t+T)= x(t)}$ for all t.

If nearby trajectories moving away from the fixed point then the point is said to be saddle point.

If the trajectories swirling around the fixed point, then it is an unstable fixed point.

If nearby trajectories moving away from the fixed point, then the point is said to be unstable fixed point.

If nearby trajectories moving towards the fixed point, then the point is said to be stable fixed point.

To check the stability of fixed point use Jacobian matrix

$\left(\begin{array}{cc}\frac{\partial \dot{x}}{\partial x}& \frac{\partial \dot{x}}{\partial y}\\ \frac{\partial \dot{y}}{\partial x}& \frac{\partial \dot{y}}{\partial y}\end{array}\right)$

The point $(x^{*},y^{*})$ is said to be a stable fixed point if eigenvalues of Jacobian matrix evaluated at this point having negative real parts and point is said to be unstable if one of its eigenvalue has positive real part. If the both eigenvalues are purely real, then the fixed point is saddle point.

Answer to Problem 7E

Solution:

The stability of the origin depends upon the values of the various parameters.

The other fixed points for the system are $\left(0,\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{ - K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{2}}}\right)$ and $\left(\frac{{\text{G}}_{\text{1}}{\text{N}}_0-{\text{K}}_1}{{\text{G}}_{\text{1}}{\text{α}}_{\text{1}}},0\right)$

The different qualitatively phase portrait are shown below.

Explanation of Solution

a)

The given system equations are

${\dot{\text{n}}}_{\text{1}}{\text{= G}}_{\text{1}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_{\text{1}}{\text{-K}}_{\text{1}}{\text{n}}_{\text{1}}$

${\dot{\text{n}}}_2{\text{= G}}_2{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_2{\text{-K}}_2{\text{n}}_2$

Fordetermining the stability of fixed point ${\text{n}}_{\text{1}}{}^{*}{\text{= n}}_{\text{2}}{}^{*}\text{= 0}$, i.e. at the origin.

Use the Jacobian matrix

The expression of the Jacobian matrix is

$\text{J = }\left(\begin{array}{cc}\frac{{\text{d}\dot{\text{n}}}_{\text{1}}}{{\text{dn}}_{\text{1}}}& \frac{{\text{d}\dot{\text{n}}}_{\text{1}}}{{\text{dn}}_{\text{2}}}\\ \frac{{\text{d}\dot{\text{n}}}_{\text{2}}}{{\text{dn}}_{\text{1}}}& \frac{{\text{d}\dot{\text{n}}}_{\text{2}}}{{\text{dn}}_{\text{2}}}\end{array}\right)$

Substitute the expressions of ${\dot{\text{n}}}_{\text{1}}$ and ${\dot{\text{n}}}_{\text{2}}$ in the above Jacobian matrix.

$\text{J = }\left(\begin{array}{cc}\frac{\text{d}\left({\text{G}}_{\text{1}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_{\text{1}}{\text{-K}}_{\text{1}}{\text{n}}_{\text{1}}\right)}{{\text{dn}}_{\text{1}}}& \frac{\text{d}\left({\text{G}}_{\text{1}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_{\text{1}}{\text{-K}}_{\text{1}}{\text{n}}_{\text{1}}\right)}{{\text{dn}}_{\text{2}}}\\ \frac{\text{d}\left({\text{G}}_2{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_2{\text{-K}}_2{\text{n}}_2\right)}{{\text{dn}}_{\text{1}}}& \frac{\text{d}\left({\text{G}}_2{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_2{\text{-K}}_2{\text{n}}_2\right)}{{\text{dn}}_{\text{2}}}\end{array}\right)$

$\text{J = }\left(\begin{array}{cc}{\text{G}}_{\text{1}}{\text{(N}}_{\text{0}}-2{\text{α}}_{\text{1}}{\text{n}}_1-{\text{α}}_{\text{2}}{\text{n}}_{\text{2}})-{\text{K}}_1& -{\text{α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{G}}_1\\ -{\text{α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{G}}_{\text{2}}& {\text{G}}_2{\text{(N}}_{\text{0}}-{\text{α}}_{\text{1}}{\text{n}}_1-2{\text{α}}_{\text{2}}{\text{n}}_{\text{2}})-{\text{K}}_2\end{array}\right)$

The above Jacobian matrix at the origin becomes,

$\text{J}\text{= }\left(\begin{array}{cc}{\text{G}}_{\text{1}}{\text{N}}_{\text{0}}-{\text{K}}_1& 0\\ 0& {\text{G}}_2{\text{N}}_{\text{0}}-{\text{K}}_2\end{array}\right)$

The eigenvalues of the above Jacobian matrix are

${\lambda }_1={\text{G}}_{\text{1}}{\text{N}}_{\text{0}}-{\text{K}}_1$

${\lambda }_2{\text{= G}}_2{\text{N}}_{\text{0}}-{\text{K}}_2$

From the above expressions of eigenvalues, the origin is unstable, if ${\lambda }_1,{\lambda }_2$ is greater than zero,

${\text{λ}}_{\text{1}}\text{> 0}$ ${\text{λ}}_2\text{> 0}$

$\therefore 0>{\text{G}}_{\text{1}}{\text{N}}_{\text{0}}-{\text{K}}_1\Rightarrow {\text{G}}_{\text{1}}{\text{N}}_{\text{0}}>{\text{K}}_1$

$\therefore {\text{0 > G}}_2{\text{N}}_{\text{0}}-{\text{K}}_2\Rightarrow {\text{G}}_2{\text{N}}_{\text{0}}>{\text{K}}_2$

And the origin is stable point if ${\lambda }_1,{\lambda }_2$ is less than zero.

${\text{λ}}_{\text{1}}\text{< 0}$ ${\text{λ}}_2\text{< 0}$

$\therefore {\text{G}}_{\text{1}}{\text{N}}_{\text{0}}{\text{-K}}_{\text{1}}\text{< 0}\Rightarrow {\text{G}}_{\text{1}}{\text{N}}_{\text{0}}{\text{< K}}_{\text{1}}$

$\therefore {\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{-K}}_{\text{2}}\text{< 0}\Rightarrow {\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{< K}}_{\text{2}}$

Thus, the system is stable at origin the value of ${\text{G}}_{\text{1}}$ and ${\text{G}}_2$ is

${\text{G}}_{\text{1}}\text{<}\frac{{\text{K}}_{\text{1}}}{{\text{N}}_{\text{0}}}$ and ${\text{G}}_{\text{2}}\text{<}\frac{{\text{K}}_{\text{2}}}{{\text{N}}_{\text{0}}}$

(b)

To estimate the other fixed point of the system put ${\dot{\text{n}}}_1=0$ and ${\dot{\text{n}}}_2=0$ in the system equations

Putting ${\dot{\text{n}}}_1=0$ in ${\dot{\text{n}}}_{\text{1}}{\text{= G}}_{\text{1}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_{\text{1}}{\text{-K}}_{\text{1}}{\text{n}}_{\text{1}}$ and ${\dot{\text{n}}}_2=0$ in ${\dot{\text{n}}}_2{\text{= G}}_2{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_2{\text{-K}}_2{\text{n}}_2$

${\text{G}}_{\text{1}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_{\text{1}}{\text{-K}}_{\text{1}}{\text{n}}_{\text{1}}\text{= 0}$

${\text{(G}}_{\text{1}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)-K}}_{\text{1}}{\text{)n}}_{\text{1}}\text{= 0}$

From the above equation, two conditions are determined.

$\therefore {\text{n}}_{\text{1}}\text{= 0}$

$\therefore {\text{G}}_{\text{1}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)-K}}_{\text{1}}\text{= 0}$

Put ${\dot{\text{n}}}_2=0$ in ${\dot{\text{n}}}_2{\text{= G}}_2{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_2{\text{-K}}_2{\text{n}}_2$

${\text{G}}_{\text{2}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_{\text{2}}{\text{-K}}_{\text{2}}{\text{n}}_{\text{2}}\text{= 0}$

${\text{(G}}_{\text{2}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)-K}}_{\text{2}}{\text{)n}}_{\text{2}}\text{= 0}$

From the above equation, two conditions are determined.

$\therefore {\text{n}}_{\text{2}}=0$

$\therefore {\text{G}}_{\text{2}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)-K}}_{\text{2}}\text{= 0}$

Now, substituting ${\text{n}}_{\text{1}}\text{= 0}$ in the condition ${\text{G}}_{\text{2}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)-K}}_{\text{2}}\text{= 0}$

${\text{G}}_{\text{2}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)-K}}_{\text{2}}\text{= 0}$

${\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{- G}}_{\text{2}}{\text{α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{-K}}_{\text{2}}\text{= 0}$

${\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{ - K}}_{\text{2}}{\text{= G}}_{\text{2}}{\text{α}}_{\text{2}}{\text{n}}_{\text{2}}\Rightarrow {\text{n}}_{\text{2}}=\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{ - K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{2}}}$

Thus, the one of the fixed point is $\left(0,\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{ - K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{2}}}\right)$

Now, substituting ${\text{n}}_2\text{= 0}$ in the condition ${\text{G}}_{\text{1}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)-K}}_{\text{1}}\text{= 0}$

${\text{G}}_{\text{1}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{)-K}}_{\text{1}}\text{= 0}$

$\therefore {\text{n}}_{\text{1}}\text{=}\frac{{\text{G}}_{\text{1}}{\text{N}}_0-{\text{K}}_1}{{\text{G}}_{\text{1}}{\text{α}}_{\text{1}}}$

Thus, the another fixed point is at $\left(\frac{{\text{G}}_{\text{1}}{\text{N}}_0-{\text{K}}_1}{{\text{G}}_{\text{1}}{\text{α}}_{\text{1}}},0\right)$

Therefore, there exists another two fixed point at $\left(0,\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{ - K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{2}}}\right)$ and $\left(\frac{{\text{G}}_{\text{1}}{\text{N}}_0-{\text{K}}_1}{{\text{G}}_{\text{1}}{\text{α}}_{\text{1}}},0\right)$

To check the stability of these points, use Jacobian matrix

$\text{J = }\left(\begin{array}{cc}\frac{{\text{d}\dot{\text{n}}}_{\text{1}}}{{\text{dn}}_{\text{1}}}& \frac{{\text{d}\dot{\text{n}}}_{\text{1}}}{{\text{dn}}_{\text{2}}}\\ \frac{{\text{d}\dot{\text{n}}}_{\text{2}}}{{\text{dn}}_{\text{1}}}& \frac{{\text{d}\dot{\text{n}}}_{\text{2}}}{{\text{dn}}_{\text{2}}}\end{array}\right)$

Let’s check the stability of the fixed point $\left(0,\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{ - K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{2}}}\right)$

Substituting expression of ${\dot{\text{n}}}_{\text{1}}$ and ${\dot{\text{n}}}_{\text{2}}$ in Jacobian matrix,

$\text{J = }\left(\begin{array}{cc}\frac{\text{d}\left({\text{G}}_{\text{1}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_{\text{1}}{\text{-K}}_{\text{1}}{\text{n}}_{\text{1}}\right)}{{\text{dn}}_{\text{1}}}& \frac{\text{d}\left({\text{G}}_{\text{1}}{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_{\text{1}}{\text{-K}}_{\text{1}}{\text{n}}_{\text{1}}\right)}{{\text{dn}}_{\text{2}}}\\ \frac{\text{d}\left({\text{G}}_2{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_2{\text{-K}}_2{\text{n}}_2\right)}{{\text{dn}}_{\text{1}}}& \frac{\text{d}\left({\text{G}}_2{\text{(N}}_{\text{0}}{\text{- α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{- α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{)n}}_2{\text{-K}}_2{\text{n}}_2\right)}{{\text{dn}}_{\text{2}}}\end{array}\right)$

$\text{J = }\left(\begin{array}{cc}{\text{G}}_{\text{1}}{\text{(N}}_{\text{0}}-2{\text{α}}_{\text{1}}{\text{n}}_1-{\text{α}}_{\text{2}}{\text{n}}_{\text{2}})-{\text{K}}_1& -{\text{α}}_{\text{2}}{\text{n}}_{\text{2}}{\text{G}}_1\\ -{\text{α}}_{\text{1}}{\text{n}}_{\text{1}}{\text{G}}_{\text{2}}& {\text{G}}_2{\text{(N}}_{\text{0}}-{\text{α}}_{\text{1}}{\text{n}}_1-2{\text{α}}_{\text{2}}{\text{n}}_{\text{2}})-{\text{K}}_2\end{array}\right)$

By substituting $\left({\text{n}}_{\text{1}}{\text{,n}}_{\text{2}}\right)=\left(0,\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{ - K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{2}}}\right)$

${\text{J}}_{\left(\text{0 ,}\frac{{\text{G}}_{\text{1}}{\text{N}}_{\text{0}}{\text{- K}}_{\text{1}}}{{\text{G}}_{\text{1}}{\text{α}}_{\text{2}}}\right)}\text{=}\left(\begin{array}{cc}{\text{G}}_{\text{1}}\left({\text{N}}_{\text{0}}-2{\text{α}}_{\text{1}}(0)-{\text{α}}_{\text{2}}\left(\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{ - K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{2}}}\right)\right)-{\text{K}}_1& -{\text{α}}_{\text{2}}\left(\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{ - K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{2}}}\right){\text{G}}_1\\ 0& {\text{G}}_2\left({\text{N}}_{\text{0}}-{\text{α}}_{\text{1}}(0)-2{\text{α}}_{\text{2}}\left(\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{ - K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{2}}}\right)\right)-{\text{K}}_2\end{array}\right)$

${\text{J}}_{\left(\text{0 ,}\frac{{\text{G}}_{\text{1}}{\text{N}}_{\text{0}}{\text{- K}}_{\text{1}}}{{\text{G}}_{\text{1}}{\text{α}}_{\text{2}}}\right)}\text{=}\left(\begin{array}{cc}\frac{{\text{G}}_{\text{1}}{\text{K}}_{\text{2}}}{{\text{G}}_{\text{2}}}-{\text{K}}_1& -{\text{G}}_{\text{1}}{\text{N}}_{\text{0}}\text{+}\frac{{\text{G}}_{\text{1}}{\text{K}}_{\text{2}}}{{\text{G}}_{\text{2}}}\\ 0& {\text{- G}}_2{N}_0{\text{+K}}_2\end{array}\right)$

The Jacobian matrix at the point $\left(\frac{{\text{G}}_{\text{1}}{\text{N}}_0-{\text{K}}_1}{{\text{G}}_{\text{1}}{\text{α}}_{\text{1}}},0\right)$ is

${\text{J}}_{\left(\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{-K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{1}}},0\right)}\text{ = }\left(\begin{array}{cc}{\text{G}}_{\text{1}}\left({\text{N}}_{\text{0}}-2{\text{α}}_{\text{1}}\left(\frac{{\text{G}}_{\text{1}}{\text{N}}_0-{\text{K}}_1}{{\text{G}}_{\text{1}}{\text{α}}_{\text{1}}}\right)-{\text{α}}_{\text{2}}\left(0\right)\right)-{\text{K}}_1& -{\text{α}}_{\text{2}}\left(0\right){\text{G}}_1\\ -{\text{α}}_{\text{1}}\left(\frac{{\text{G}}_{\text{1}}{\text{N}}_0-{\text{K}}_1}{{\text{G}}_{\text{1}}{\text{α}}_{\text{1}}}\right){\text{G}}_{\text{2}}& {\text{G}}_2\left({\text{N}}_{\text{0}}-{\text{α}}_{\text{1}}\left(\frac{{\text{G}}_{\text{1}}{\text{N}}_0-{\text{K}}_1}{{\text{G}}_{\text{1}}{\text{α}}_{\text{1}}}\right)-2{\text{α}}_{\text{2}}\left(0\right)\right)-{\text{K}}_2\end{array}\right)$

${\text{J}}_{\left(\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{-K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{1}}},0\right)}\text{ = }\left(\begin{array}{cc}{\text{G}}_{\text{1}}{\text{N}}_{\text{0}}{\text{+ K}}_1& 0\\ -{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}+\frac{{\text{G}}_{\text{2}}{\text{K}}_{\text{1}}}{{\text{G}}_{\text{1}}}& \frac{{\text{G}}_{\text{2}}{\text{K}}_{\text{1}}}{{\text{G}}_{\text{1}}}-{\text{K}}_2\end{array}\right)$

Here, the Jacobian matrixes are triangular matrix.

${\text{J}}_{\left(\text{0 ,}\frac{{\text{G}}_{\text{1}}{\text{N}}_{\text{0}}{\text{- K}}_{\text{1}}}{{\text{G}}_{\text{1}}{\text{α}}_{\text{2}}}\right)}\text{=}\left(\begin{array}{cc}\frac{{\text{G}}_{\text{1}}{\text{K}}_{\text{2}}}{{\text{G}}_{\text{2}}}-{\text{K}}_1& -{\text{G}}_{\text{1}}{\text{N}}_{\text{0}}\text{+}\frac{{\text{G}}_{\text{1}}{\text{K}}_{\text{2}}}{{\text{G}}_{\text{2}}}\\ 0& {\text{- G}}_2{N}_0{\text{+K}}_2\end{array}\right)$ is a upper triangular matrix.

And

${\text{J}}_{\left(\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{-K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{1}}},0\right)}\text{ = }\left(\begin{array}{cc}{\text{G}}_{\text{1}}{\text{N}}_{\text{0}}{\text{+ K}}_1& 0\\ -{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}+\frac{{\text{G}}_{\text{2}}{\text{K}}_{\text{1}}}{{\text{G}}_{\text{1}}}& \frac{{\text{G}}_{\text{2}}{\text{K}}_{\text{1}}}{{\text{G}}_{\text{1}}}-{\text{K}}_2\end{array}\right)$ is lower triangular matrix.

The eigenvalues of the triangular matrix are the diagonal elements.

Thus, the eigenvalues of Jacobian matrix ${\text{J}}_{\left(\text{0 ,}\frac{{\text{G}}_{\text{1}}{\text{N}}_{\text{0}}{\text{- K}}_{\text{1}}}{{\text{G}}_{\text{1}}{\text{α}}_{\text{2}}}\right)}$ are

${\lambda }_1=\frac{{\text{G}}_{\text{1}}{\text{K}}_{\text{2}}}{{\text{G}}_{\text{2}}}-{\text{K}}_1$ and ${\lambda }_2{\text{= - G}}_2{N}_0{\text{+K}}_2$

The stability of the fixed point $\left(0,\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{ - K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{2}}}\right)$ is depends on the values of ${\text{G}}_{\text{1}}{\text{,G}}_{\text{2}}{\text{,N}}_{\text{0}}{\text{,K}}_{\text{1}}{\text{,K}}_{\text{2}}$

Both the eigenvalues have negative real parts. Hence the fixed point is stable.

If one of the eigenvalue has positive real part and another having negative real part, then the fixed point is saddle fixed point. If both eigenvalues have positive real part, then the fixed point is unstable.

And eigenvalues of Jacobian matrix ${\text{J}}_{\left(\frac{{\text{G}}_{\text{2}}{\text{N}}_{\text{0}}{\text{-K}}_{\text{2}}}{{\text{G}}_{\text{2}}{\text{α}}_{\text{1}}},0\right)}$ are

${\lambda }_1{\text{= G}}_{\text{1}}{\text{N}}_{\text{0}}{\text{+ K}}_1$ and ${\lambda }_2=\frac{{\text{G}}_{\text{2}}{\text{K}}_{\text{1}}}{{\text{G}}_{\text{1}}}-{\text{K}}_2$

The stability of the fixed point $\left(\frac{{\text{G}}_{\text{1}}{\text{N}}_0-{\text{K}}_1}{{\text{G}}_{\text{1}}{\text{α}}_{\text{1}}},0\right)$ is dependent on the values of ${\text{G}}_{\text{1}}{\text{,G}}_{\text{2}}{\text{,N}}_{\text{0}}{\text{,K}}_{\text{1}}{\text{,K}}_{\text{2}}$

If the both the eigenvalues have negative real parts, then the fixed point is stable.

If one of the eigenvalue has positive real part and another having negative real part, then the fixed point is saddle fixed point. If both eigenvalues have positive real part, then the fixed point is unstable.

(c) The different phase portrait for the different value of the parameter constant is plotted as:

Considering a constant parameter is as follows:

${\text{N}}_{\text{0}}\text{=5}$, ${\text{G}}_{\text{1}}\text{=1}$, ${\text{G}}_{\text{2}}\text{=1}$, ${\text{α}}_{\text{1}}\text{=1}$, ${\text{α}}_2\text{=1}$, ${\text{K}}_{\text{1}}\text{= 7}\text{.5}$, ${\text{K}}_{\text{2}}\text{= 7}\text{.5}$

${\dot{\text{n}}}_{\text{1}}{\text{= 1(5- n}}_{\text{1}}{\text{- n}}_{\text{2}}{\text{)n}}_{\text{1}}\text{-7}{\text{.5n}}_{\text{1}}$

${\dot{\text{n}}}_2{\text{= (5- n}}_{\text{1}}{\text{- n}}_{\text{2}}{\text{)n}}_2\text{-7}{\text{.5n}}_2$

The phase portrait for the above constant value is plotted as follows:

This phase portrait describes that ${\text{n}}_{\text{1}}{\text{ and n}}_{\text{2}}$ are decaying to origin.

Considering a constant parameter is as follows:

${\text{N}}_{\text{0}}\text{=5}$, ${\text{G}}_{\text{1}}\text{=1}$, ${\text{G}}_{\text{2}}\text{=1}$, ${\text{α}}_{\text{1}}\text{=1}$, ${\text{α}}_2\text{=1}$, ${\text{K}}_{\text{1}}\text{= 7}\text{.5}$, ${\text{K}}_{\text{2}}\text{= 2}\text{.5}$

${\dot{\text{n}}}_{\text{1}}{\text{= 1(5- n}}_{\text{1}}{\text{- n}}_{\text{2}}{\text{)n}}_{\text{1}}\text{-7}{\text{.5n}}_{\text{1}}$

${\dot{\text{n}}}_2{\text{= (5- n}}_{\text{1}}{\text{- n}}_{\text{2}}{\text{)n}}_2\text{-2}{\text{.5n}}_2$

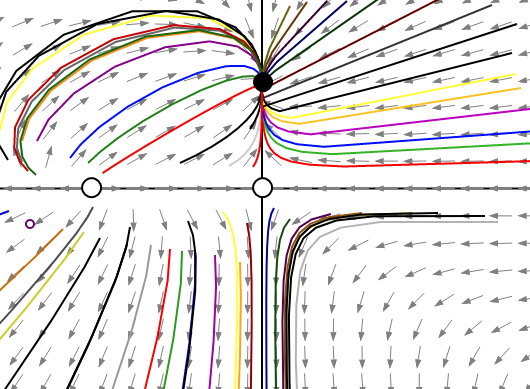
This phase portrait describes that stable point is on the ${\text{n}}_{\text{2}}$ axis.

Considering a constant parameter is as follows:

${\text{N}}_{\text{0}}\text{=5}$, ${\text{G}}_{\text{1}}\text{=1}$, ${\text{G}}_{\text{2}}\text{=1}$, ${\text{α}}_{\text{1}}\text{=1}$, ${\text{α}}_2\text{=1}$, ${\text{K}}_{\text{1}}\text{= 2}\text{.5}$, ${\text{K}}_{\text{2}}\text{= 7}\text{.5}$

${\dot{\text{n}}}_{\text{1}}{\text{= 1(5- n}}_{\text{1}}{\text{- n}}_{\text{2}}{\text{)n}}_{\text{1}}\text{-2}{\text{.5n}}_{\text{1}}$

${\dot{\text{n}}}_2{\text{= (5- n}}_{\text{1}}{\text{- n}}_{\text{2}}{\text{)n}}_2\text{-7}{\text{.5n}}_2$

The phase portrait describes that the stable point is on ${\text{n}}_{\text{1}}$ axis

${\text{N}}_{\text{0}}\text{=5}$, ${\text{G}}_{\text{1}}\text{=1}$, ${\text{G}}_{\text{2}}\text{=1}$, ${\text{α}}_{\text{1}}\text{=1}$, ${\text{α}}_2\text{=1}$, ${\text{K}}_{\text{1}}\text{= 2}\text{.5}$, ${\text{K}}_{\text{2}}\text{= 2}\text{.5}$

${\dot{\text{n}}}_{\text{1}}{\text{= 1(5- n}}_{\text{1}}{\text{- n}}_{\text{2}}{\text{)n}}_{\text{1}}\text{-2}{\text{.5n}}_{\text{1}}$

${\dot{\text{n}}}_2{\text{= (5- n}}_{\text{1}}{\text{- n}}_{\text{2}}{\text{)n}}_2\text{-2}{\text{.5n}}_2$

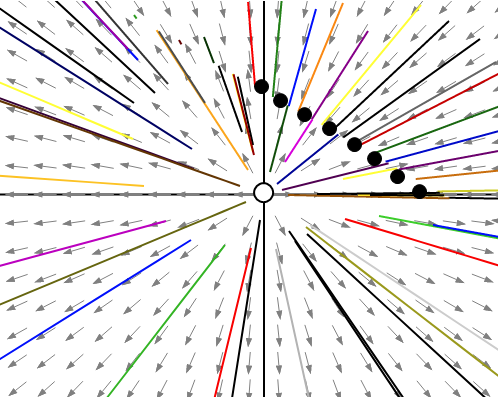
This phase portrait describes that there are infinite number of fixed points in the first quadrant of the graph and an unstable point at origin.

There are four different qualitatively phase portrait can be sketched for the system and there is no possibility of other phase portrait because the nullclines are axes and parallel lines.