Chapter 6.6, Problem 6E

Interpretation Introduction

Interpretation:

To plot the nullclines $\dot{\text{x}}\text{ = 0}$ and $\dot{\text{y}}\text{ = 0}$ for the system ${\dot{\text{x}}\text{ = y - y}}^{\text{3}}$, ${\dot{\text{y}}\text{ = - x - y}}^{\text{2}}$. To find the sign of $\dot{\text{x}}\text{, }\dot{\text{y}}$ in different regions of the plane. To find the Eigenvalues and Eigenvectors of the saddle points at $\left(\text{-1, ±1}\right)$. To prove that the unstable manifold $\left(\text{-1, -1}\right)$ intersects the negative $\text{x}$- axis. To use reversibility to prove the existence of a heteroclinic trajectory connecting $\left(\text{-1, -1}\right)$ to $\left(\text{-1, 1}\right)$. To prove that another heteroclinic trajectory exists and to sketch several other trajectories to fill in the phase portrait.

Concept Introduction:

Nullclines are the curves in the phase portrait where either $\dot{\text{x}}\text{ = 0}$ or $\dot{\text{y}}\text{ = 0}$.

Fixed points occur where $\dot{\text{x}}\text{ = 0}$ and $\dot{\text{y}}\text{ = 0}$.

The Jacobian matrix at a general point $\left(\text{x, y}\right)$ is given by

$\text{J = }\left(\begin{array}{cc}\frac{\partial \dot{\text{x}}}{\partial \text{x}}& \frac{\partial \dot{\text{x}}}{\partial \text{y}}\\ \frac{\partial \dot{\text{y}}}{\partial \text{x}}& \frac{\partial \dot{\text{y}}}{\partial \text{y}}\end{array}\right)$

The Eigenvalue $\text{λ}$ can be calculated using the characteristic equation

$\left|\left(\text{A - λI}\right)\right|\text{ = 0}$

The solution of the quadratic equation is $\text{λ = }\frac{\text{-b ± }\sqrt{{\text{b}}^{\text{2}}\text{- 4ac}}}{\text{2a}}$

The unstable manifold for a fixed point is the set of all points in the plane which tend to the fixed point as time goes to negative infinity.

Answer to Problem 6E

Solution:

a) The nullclines $\dot{\text{x}}\text{ = 0}$ and $\dot{\text{y}}\text{ = 0}$ for the given system are plotted.

b) The sign of $\dot{\text{x}}$ and $\dot{\text{y}}$ in different regions of the plane is shown in the nullcline plot.

c) The Eigenvalues and Eigenvectors of the saddle points at $\left(\text{-1, ±1}\right)$ are calculated.

d) It is proved that the unstable manifold $\left(\text{-1, -1}\right)$ intersects the negative $\text{x}$- axis. It is proved that the heteroclinic trajectory exists, connecting $\left(\text{-1, -1}\right)$ to $\left(\text{-1, 1}\right)$.

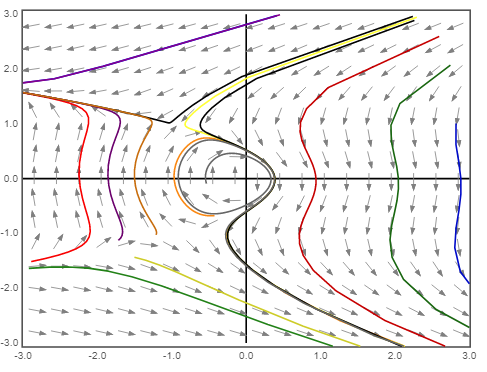
e) The phase portrait for the given system is plotted.

Explanation of Solution

a) The system is given as

${\dot{\text{x}}\text{ = y - y}}^{\text{3}}$, ${\dot{\text{y}}\text{ = - x - y}}^{\text{2}}$

Nullclines are the curves in the phase portrait where either $\dot{\text{x}}\text{ = 0}$ or $\dot{\text{y}}\text{ = 0}$.

Substituting $\dot{\text{x}}\text{ = 0}$ in the above system,

${\text{y - y}}^{\text{3}}\text{ = 0}$

$\text{y}\left({\text{1 - y}}^{\text{2}}\right)\text{ = 0}$

$\text{y = 0}$ and $\left({\text{1 - y}}^{\text{2}}\right)\text{ = 0 }\Rightarrow \text{ y = }\pm \text{1}$

Thus,

$\text{y = 0, 1, -1}$.

Substituting $\dot{\text{y}}\text{ = 0}$ in the above system,

$\begin{array}{l}{\text{- x - y}}^{\text{2}}\text{ = 0}\\ \text{y = ±}\sqrt{\text{-x}}\end{array}$

Therefore, the nullclines of the given system are

$\begin{array}{l}\text{y = 0, 1, -1}\\ \text{y = ±}\sqrt{\text{-x}}\end{array}$

The nullclines plot for the given system equation is shown below:

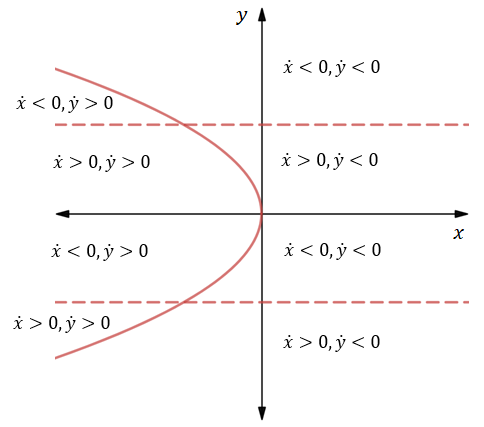
b) The value of the system at $\dot{\text{x}}$ and $\dot{\text{y}}$ lie in all the four quadrants, and it depends on the value of the initial conditions of the system.

The sign of $\dot{\text{x}}$ and $\dot{\text{y}}$ in different regions of the plane is shown in the above nullcline plot.

c) The fixed points of the system would be where $\dot{\text{x}}\text{ = 0}$ and $\dot{\text{y}}\text{ = 0}$.

The fixed points can be obtained by substituting $\dot{\text{x}}\text{ = 0}$ and $\dot{\text{y}}\text{ = 0}$ in the given system.

Therefore, the fixed points are $\left(\text{0, 0}\right)$ $\left(\text{-1, 1}\right)$ and $\left(\text{-1, -1}\right)$.

The Jacobian matrix at a general point $\left(\text{x, y}\right)$ is given by

$\text{J = }\left(\begin{array}{cc}\frac{\partial \dot{\text{x}}}{\partial \text{x}}& \frac{\partial \dot{\text{x}}}{\partial \text{y}}\\ \frac{\partial \dot{\text{y}}}{\partial \text{x}}& \frac{\partial \dot{\text{y}}}{\partial \text{y}}\end{array}\right)$

Substituting the given system in the Jacobian matrix,

$\text{J = }\left(\begin{array}{cc}\frac{\partial \left({\text{y - y}}^{\text{3}}\right)}{\partial \text{x}}& \frac{\partial \left({\text{y - y}}^{\text{3}}\right)}{\partial \text{y}}\\ \frac{\partial \left({\text{- x - y}}^{\text{2}}\right)}{\partial \text{x}}& \frac{\partial \left({\text{- x - y}}^{\text{2}}\right)}{\partial \text{y}}\end{array}\right)$

$\text{J = }\left(\begin{array}{cc}\text{0}& {\text{1 - 3y}}^{\text{2}}\\ \text{-1}& \text{- 2y}\end{array}\right)$

The value of the Jacobian matrix at the fixed point $\left(\text{0, 0}\right)$ is

${\text{J}}_{\left(\text{0, 0}\right)}\text{ = }\left(\begin{array}{cc}\text{0}& \text{1}\\ \text{-1}& \text{0}\end{array}\right)$

Therefore, from the Jacobian matrix, it is clear that the fixed point $\left(\text{0, 0}\right)$ is a clockwise center.

The value of the Jacobian matrix at the fixed point $\left(\text{-1, 1}\right)$ is

${\text{J}}_{\left(\text{-1, 1}\right)}\text{ = }\left(\begin{array}{cc}\text{0}& \text{-2}\\ \text{-1}& \text{-2}\end{array}\right)$

The value of the Jacobian matrix at the fixed point $\left(\text{-1, -1}\right)$ is

${\text{J}}_{\left(\text{-1, 1}\right)}\text{ = }\left(\begin{array}{cc}\text{0}& \text{-2}\\ \text{-1}& \text{2}\end{array}\right)$

The Eigenvalue $\text{λ}$ can be calculated using the characteristic equation

$\left|\left(\text{A - λI}\right)\right|\text{ = 0}$

To find the Eigenvalues and the Eigenvectors of the Jacobian matrix ${\text{J}}_{\left(\text{-1,1}\right)}$, substitute $\text{J = }\left(\begin{array}{cc}\text{0}& \text{-2}\\ \text{-1}& \text{-2}\end{array}\right)$ and $\text{I = }\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$,

$\left(\begin{array}{cc}\text{0}& \text{-2}\\ \text{-1}& \text{-2}\end{array}\right)\text{ - λ}\left(\begin{array}{cc}\text{1}& \text{0}\\ \text{0}& \text{1}\end{array}\right)\text{ = 0}$

$\left(\begin{array}{cc}\text{-λ}& \text{-2}\\ \text{-1}& \text{-2 - λ}\end{array}\right)\text{ = 0}$

The determinant of the above matrix is

${\text{Δ}}_{\left(\text{-1,1}\right)}\text{ = -λ}\left(\text{-2 - λ}\right)\text{ - 2}$

From the above matrix,

${\text{λ}}^{\text{2}}\text{ + 2λ - 2 = 0}$

The above quadratic equation can be solved by using $\text{λ = }\frac{\text{-b ± }\sqrt{{\text{b}}^{\text{2}}\text{- 4ac}}}{\text{2a}}$

$\text{λ = }\frac{\text{-2 ± }\sqrt{{\text{2}}^{\text{2}}\text{-}\left(\text{4}\right)\left(\text{-2}\right)}}{\text{2}}$

$\text{λ = -1 ± }\sqrt{\text{3}}$

Therefore, the Eigenvalue of the Jacobian matrix ${\text{J}}_{\left(\text{-1, 1}\right)}$ is $\text{λ = -1 ± }\sqrt{\text{3}}$

The corresponding Eigenvectors for the above Jacobian matrix ${\text{J}}_{\left(\text{-1, 1}\right)}$ are

$\begin{array}{l}{\text{v}}_{\text{1}}\text{ = }\left(\begin{array}{c}\text{1}\\ \frac{\text{1 - }\sqrt{\text{3}}}{\text{2}}\end{array}\right)\\ {\text{v}}_{\text{2}}\text{ = }\left(\begin{array}{c}\text{1}\\ \frac{\text{1 + }\sqrt{\text{3}}}{\text{2}}\end{array}\right)\end{array}$

Similarly, to find the Eigenvalues and the Eigenvectors of the Jacobian matrix ${\text{J}}_{\left(\text{-1, -1}\right)}$, substitute $\text{J = }\left(\begin{array}{cc}\text{0}& \text{-2}\\ \text{-1}& \text{2}\end{array}\right)$ and $\text{I = }\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$,

$\left(\begin{array}{cc}\text{0}& \text{-2}\\ \text{-1}& \text{2}\end{array}\right)\text{ - λ}\left(\begin{array}{cc}\text{1}& \text{0}\\ \text{0}& \text{1}\end{array}\right)\text{ = 0}$

$\left(\begin{array}{cc}\text{-λ}& \text{-2}\\ \text{-1}& \text{2 - λ}\end{array}\right)\text{ = 0}$

The determinant of the above matrix is

${\text{Δ}}_{\left(\text{-1, -1}\right)}\text{ = -λ}\left(\text{2 - λ}\right)\text{ - 2}$

From the above matrix,

${\text{λ}}^{\text{2}}\text{ - 2λ - 2 = 0}$

The above quadratic equation can be solved by using $\text{λ = }\frac{\text{-b ± }\sqrt{{\text{b}}^{\text{2}}\text{- 4ac}}}{\text{2a}}$

$\text{λ = }\frac{\text{- (-2) ± }\sqrt{{\left(\text{-2}\right)}^{\text{2}}\text{-}\left(\text{4}\right)\left(\text{-2}\right)}}{\text{2}}$

$\text{λ = 1 ± }\sqrt{\text{3}}$

Therefore, the Eigenvalue of the Jacobian matrix ${\text{J}}_{\left(\text{-1, -1}\right)}$ is $\text{λ = 1 ± }\sqrt{\text{3}}$

The corresponding Eigenvectors for the above Jacobian matrix ${\text{J}}_{\left(\text{-1, -1}\right)}$ are

$\begin{array}{l}{\text{v}}_{\text{1}}\text{ = }\left(\begin{array}{c}\text{1}\\ \frac{\text{1 - }\sqrt{\text{3}}}{\text{-2}}\end{array}\right)\\ {\text{v}}_{\text{2}}\text{ = }\left(\begin{array}{c}\text{1}\\ \frac{\text{1 + }\sqrt{\text{3}}}{\text{-2}}\end{array}\right)\end{array}$

d) The unstable manifold for a fixed point is the set of all points in the plane which tend to the fixed point as time goes to negative infinity.

Consider the unstable manifold of the saddle point $\left(\text{-1, -1}\right)$. The part of the unstable manifold lies in the region where $\dot{\text{x}}\text{ < 0, }\dot{\text{y}}\text{ > 0}$. A phase point along the manifold will move up and to the left and eventually will cut the negative $\text{x}$- axis.

Since the system is reversible under the transformation $\text{t}\to \text{ -t}$, $\text{y}\to \text{ -y}$. By reversibility, there must be a twin trajectory with the same endpoint on the negative $\text{x}$- axis from $\left(\text{1, 1}\right)$ but with arrow reversed. Together the two trajectories form a heteroclinic orbit.

e) Consider the unstable manifold of the saddle point $\left(\text{-1, 1}\right)$. The part of the unstable manifold lies in the region where $\dot{\text{x}}\text{ > 0, }\dot{\text{y}}\text{ < 0}$. A phase point along the manifold will move down and to the right and eventually will cut the positive $\text{x}$- axis.

Since the system is reversible under the transformation $\text{t}\to \text{ -t}$, $\text{y}\to \text{ -y}$. By reversibility, there must be a twin trajectory with the same endpoint on the positive $\text{x}$- axis from $\left(\text{1, -1}\right)$ but with arrow reversed. Together the two trajectories form another heteroclinic orbit.

The phase portrait of the given system is shown below: