
Concept explainers
Find the equations for slope and deflection of the beam using direct integration method.
Answer to Problem 6P
For segment AB:
The equation for slope is
The equation for deflection is
For segment BC:
The equation for slope is
The equation for deflection is
Explanation of Solution
Calculation:
Consider flexural rigidity EI of the beam is constant.
Draw the free body diagram of the beam as in Figure (1).
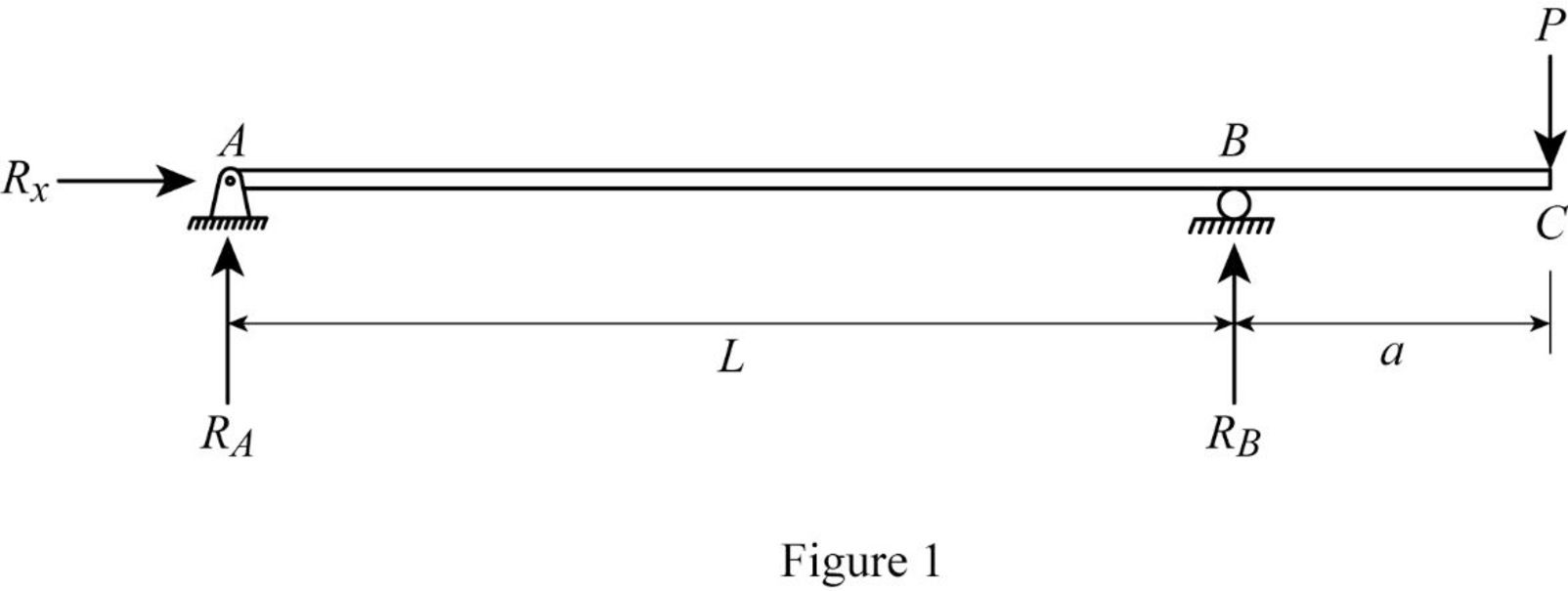
Refer Figure (1),
Consider upward force is positive and downward force is negative.
Consider clockwise is negative and counterclowise is positive.
Determine the support reaction at A using the relation;
Determine the support reaction at B using the relation;
Show the reaction values as in Figure (2).

Take a section at a distance of x.
Show the section as in Figure (2).
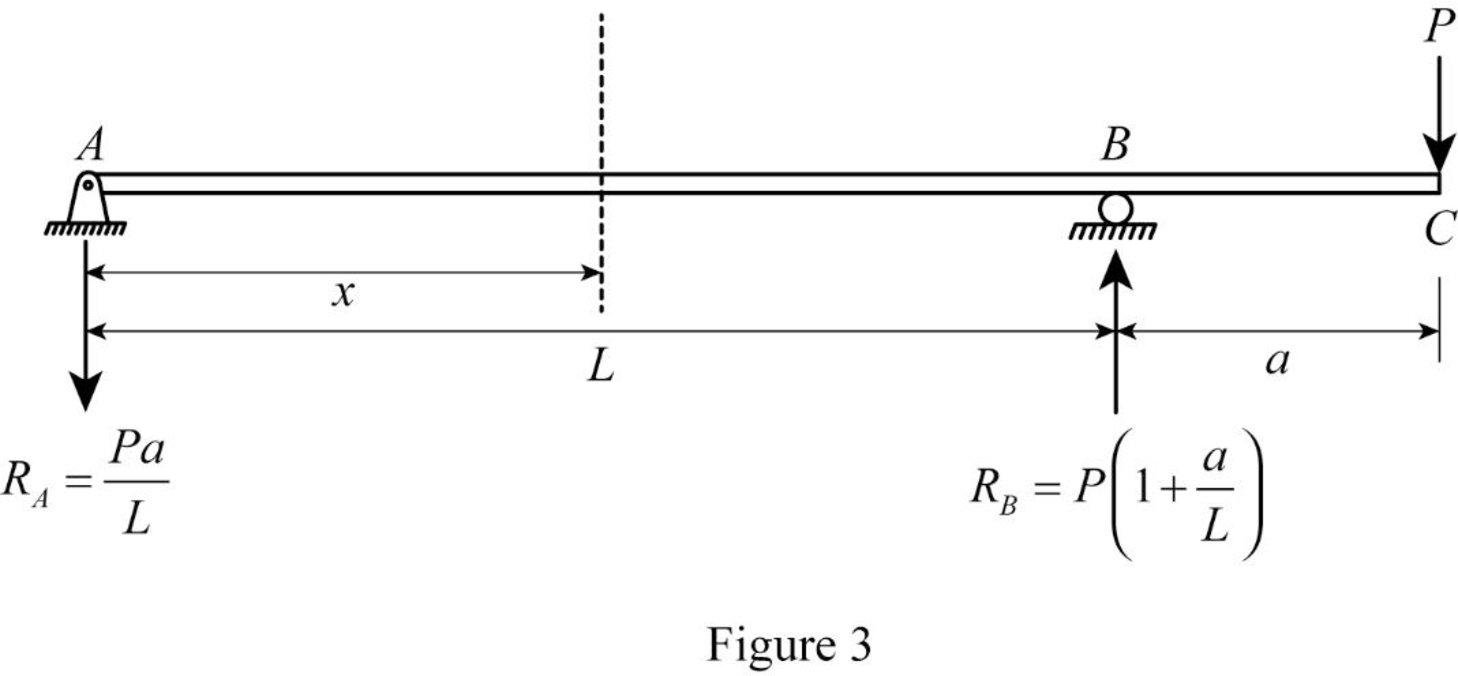
Consider the segment AB:
Refer Figure (2),
Write the equation for bending moment at x distance.
Write the equation for
Write the equation for slope as follows:
Integrate Equation (1) with respect to x.
Write the equation for deflection as follows:
Integrate Equation (2) with respect to x.
Find the integration constants
Write the boundary conditions as follows:
Apply the above boundary conditions in Equation (3):
Write the boundary conditions as follows:
Apply the above boundary conditions in Equation (3):
Find the equation for slope.
Substitute
Thus, the equation for slope is
Find the equation for deflection.
Substitute
Thus, the equation for deflection is
Consider segment BC;
Show the distance at a distance of x as in Figure (4).
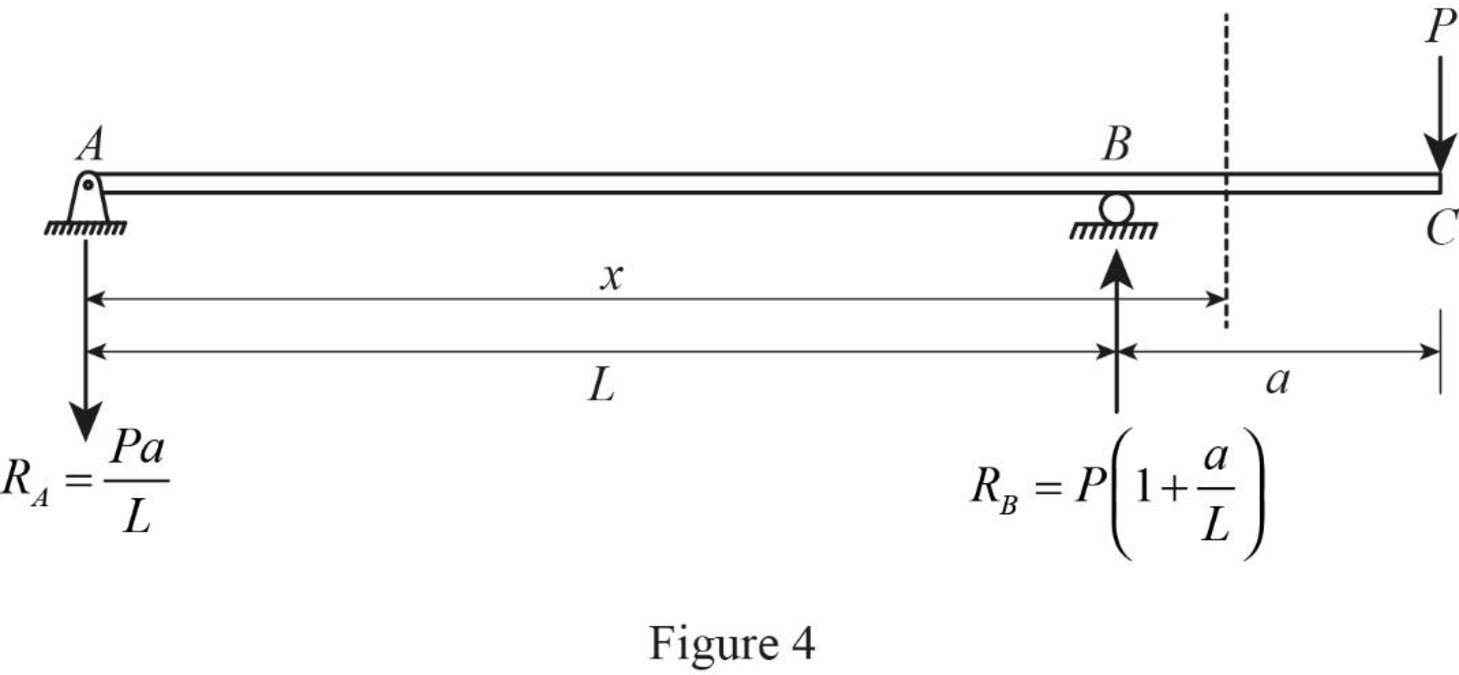
Refer Figure (2),
For segment BC the limit should be
Write the equation for bending moment at x distance.
Write the equation for
Write the equation for slope as follows:
Integrate Equation (4) with respect to x.
Write the equation for deflection as follows:
Integrate Equation (5) with respect to x.
Write the boundary conditions as follows:
The slope at left and right of support B is equal.
Substitute
Apply the above boundary conditions in the above Equation
Substitute
Hence, the Equation for slope is
Write the boundary conditions as follows:
Apply the above boundary conditions in Equation (6):
Substitute
Hence, the Equation for deflection is
Want to see more full solutions like this?
Chapter 6 Solutions
Structural Analysis (MindTap Course List)
- help me with this Question for revision purpose and as well with references The office building was built in year 2017 and has not obtained any Green Mark certification before. The office building is occupied by a single tenant/entity. The building management team had done an analysis of the building’s energy performance by extracting the data from the various systems. The current performance and findings of the systems are listed in Appendix A. The client is considering to have the building undergo retrofitting to improve the building’s energy performance. The objective is to achieve Green Mark Gold Plus under the new Green Mark 2021 framework. For part (a) below, you are to use Pathway 1: EUI for this. (a) As part of the feasibility exercise, you are to interpret the current performance of the existing building based on the data available (Refer to Appendix A). You should then organise and present to the client how does the current building relate to the Energy Efficiency Section of…arrow_forwardWhat are the advantages and disadvanages of using a bar chart in construction scheduling?arrow_forward1- Determine the area of the region enclosed by y = t sin(t), the x- axis, y-axis and x = Π 元-3arrow_forward
- The 4-story building shown below has a dead load D = 90 psf, floor live load, L = 110 psf. The roof and floors have the same D and L loads. The length of columns is 24 ft at the ground level and 12 ft for all other floors. The column ends are pins (Kx = Ky = 1.0) and Lx = Ly for all columns. (Use LFRD Method where applicable).1) Determine Pu on interior columns B2-4, B2-1, and side column C1-1 2) Use Table 4-1a (p. 4-12 to 4-24) in AISC to select the lightest W shapes for these columns 3) Use Table 4-4 (p. 4-68 to 4-83) in AISC to select lightest square HSS shape for the columnsarrow_forwardThe 4-story building shown below has a dead load D = 90 psf, floor live load, L = 110 psf. The roof and floors have the same D and L loads. The length of columns is 24 ft at the ground level and 12 ft for all other floors. The column ends are pins (Kx = Ky = 1.0) and Lx = Ly for all columns. Determine Pu on interior columns B2-4, B2-1, and side column C1-1 (Use LFRD where applicable).arrow_forwardProblems 5-1 Stead flow of steam enters a condenser with an enthalpy of 2400 kJ/kg and a velocity of 366 m/sec. the condensate leaves the condenser with an enthalpy of 162kJ/sec and a velocity of 6 m/sec what is the heat transferred to the cooling water per kg steam condensed. (-69198 kJ/kg) 5-2 An air compressor delivers 4.5 kg of air per minute at a pressure of 7 bar and a specific volume of 0.17 m³ /kg. Ambient conditions are pressure 1bar and specific volume 0.86 m³/kg. The initial and final internal energy values for the air are 28 kJ/kg and 110 kJ/kg respectively. Heat rejected to the cooling jacket is 76kJ/kg of air pumped. Neglecting changes in kinetic and potential energies, what is the shaft power required driving the compressor? (14.3kW)arrow_forward
