
Concept explainers
Find the equations for slope and deflection of the beam using direct integration method.
Answer to Problem 3P
The equation for slope for segment AB is
The equation for deflection for segment AB is
The equation for slope for segment BC is
The equation for deflection for segment BC is
Explanation of Solution
Calculation:
Draw the free body diagram of the beam as in Figure (1).
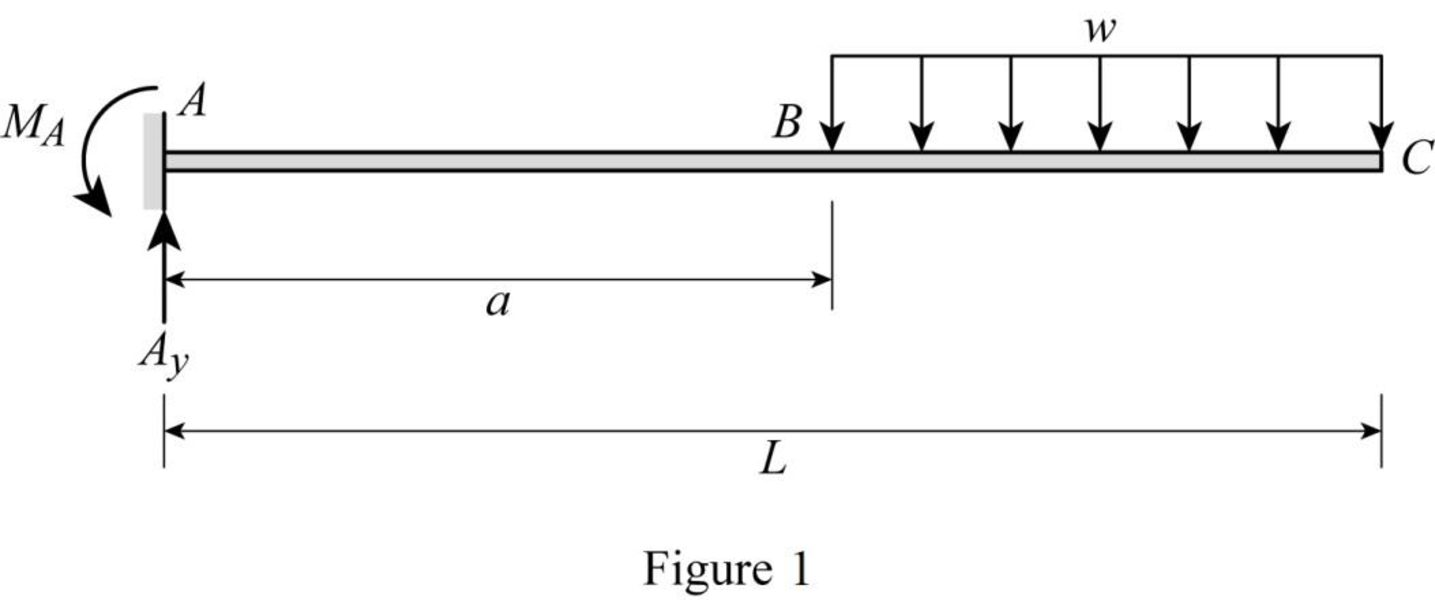
Refer Figure (1),
Find the reaction at support A.
Apply vertical equilibrium along y-axis.
Consider upward force as positive.
Find the moment at A.
Consider anticlockwise moment as positive.
Segment AB:
Consider a section
Sketch the free body diagram when section
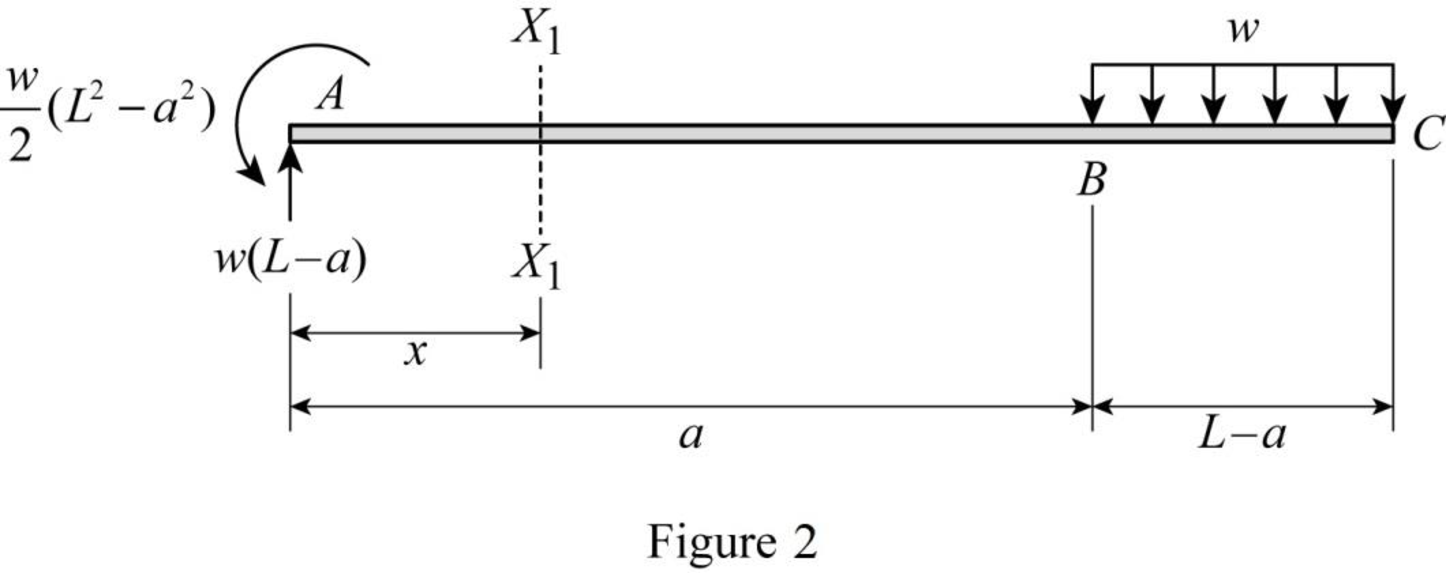
Refer Figure (2),
Take the moment at section
Write the equation for
Find the equation for slope
Integrate Equation (1) with respect to x.
Find the equation for deflection
Integrate again Equation (2) with respect to x.
Find the integration constants
Apply boundary conditions in Equation (2):
At
Apply boundary conditions in Equation (1):
At
Find the equation for slope of segment AB.
Substitute 0 for
Thus, the equation for slope of segment AB is
Find the equation for deflection of segment AB.
Substitute 0 for
Thus, the equation for deflection is
Segment BC:
Consider a section
Sketch the free body diagram when section
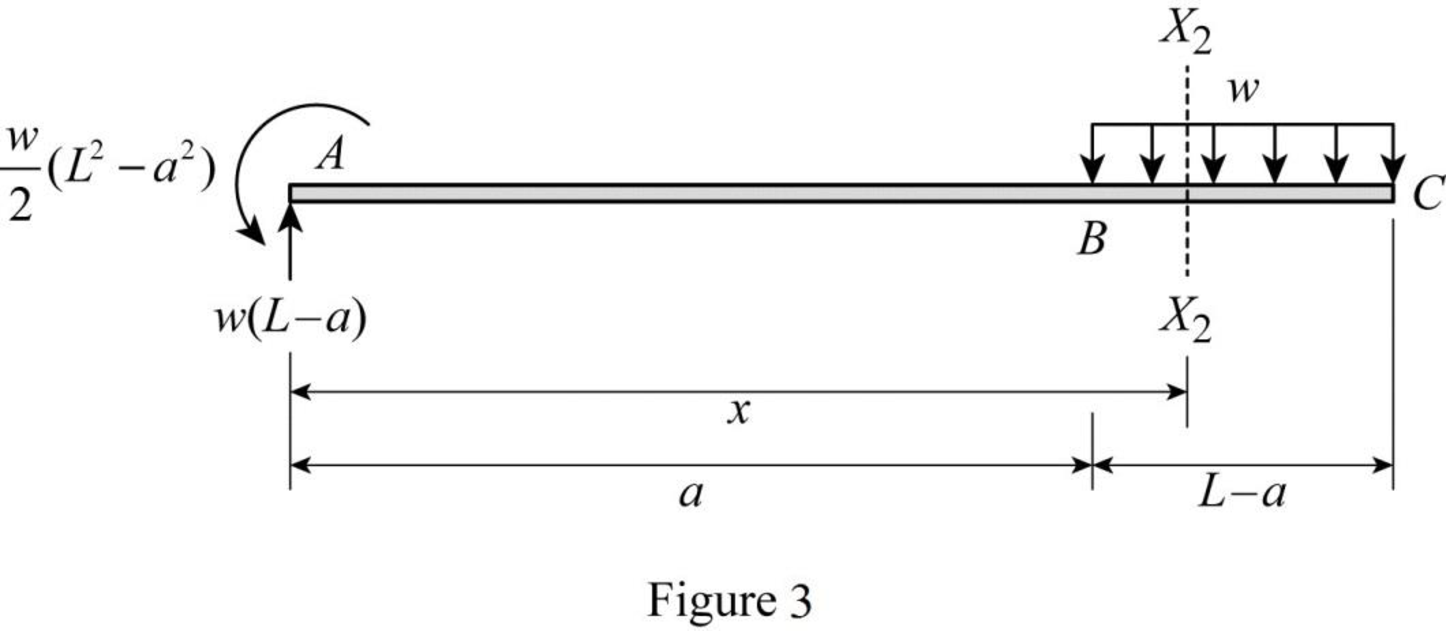
Refer Figure 3.
Write the equation for bending moment at section
Write the equation for
Write the equation for slope.
Integrate Equation (4) with respect to x.
Write the equation for deflection.
Integrate Equation (5) with respect to x.
Find the integration constants
Apply boundary conditions in Equation (3):
At
Apply boundary conditions in Equation (4):
At
Find the equation for slope of segment BC.
Substitute
Thus, the equation for slope of segment BC is
Find the equation for deflection of segment BC.
Substitute
Thus, the equation for deflection of segment BC is
Want to see more full solutions like this?
Chapter 6 Solutions
Structural Analysis (MindTap Course List)
- I need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forwardI need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forwardI need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forward
- I need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forwardI need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forwardI need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forward
- I need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forwardI need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forwardI need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forward
- I need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forwardI need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forwardI need detailed help solving this exercise from homework of Engineering Mathematics II.I do not really understand how to do, please do it step by step, not that long but clear. Thank you!P.S.: Please do not use AI, thanks!arrow_forward
