What is a Beam?

In structural engineering, a beam is a component made of a variety of materials (including steel alloys, and wood) that can resist loads applied laterally to the beam axis. Members, elements, rafters, shafts, and purlins are all terms used to describe beams.

Beam Shapes

Beams exist in a variety of forms and sizes, each with its own set of applications and strengths. I beam, T-beam, channel sections, rectangular, hollow rectangle, and pipes are some typical forms. They're all considered beams, regardless of form.

A beam is a structural element that typically resists loads that are applied laterally to the axis of the beam. Its primary mode of deflection is bending. As a consequence of the loads imparted to a beam, reaction forces are generated at its supports. A beam is a structural element that can withstand load through resisting bending forces.

They're utilized to transfer traffic across shorter intervals. Reaction forces are generated at the beam's support points as a result of the loads applied to it. All of the forces operating on the beam combine to produce shear forces and bending moments within the beam, which result in internal forces or internal tensile or compressive stresses, strains, and deflections or deformation. Beams are distinguished by their support method, profile (cross-section form), equilibrium conditions, length, and material.

Shear forces and bending moments

Shear forces and bending moments are produced when finite loads apply Linear as well as transverse analysis to the longitudinal axis. The main source of beam bending is the lateral load analysis applied mostly on beams. They're in charge of moving a weight from a slab to a column. The load distribution pattern is,

Slab =>Beam=> Column =>Foundation

Direct support refers to the link between the beam and the column, whereas indirect support refers to the connection between the beam and box beam. All of the forces operating on the beam result in shear forces and bending moments within the beams, which cause internal stresses, strains, and deflections mostly in the beam. Beams are commonly used to describe the building or civil engineering solid structural elements, however, any structures which contain beam structures built to transport lateral loads, including such automobile frames, aircraft components, machine frames, wood beams, and some other mechanical or structural systems, are analyzed in much the same way. The horizontal beam carries solely a transverse load, while the sloping beams support both transverse and axial loads.

Purpose of Beams and standard sizes

It's a load-bearing structural member that can withstand loads by resisting bending stresses. Steel, reinforced concrete (RCC), or steel (or other metal) are used to construct them. It's utilized in construction to resist loads, counter bending moments and shear stresses, connect the frames and distribute loads evenly. To counteract the shear stress, stirrups are utilized. Shear reinforcement in the beam is another name for it.

The shear force is greatest at the ends of the beams (simply supported beams) and zero in the middle. As a result, the spacing of stirrups or rings (or circular radius )at either end is narrower than in the middle. Stirrups are rectangular in design, with reinforcing bars wrapped around the top and bottom bars of the beam. Stirrups are sometimes installed diagonally and vertically to prevent shear failure in the event of beam cracks.

The Different reinforcements were utilized in the beam for various purposes, including discussed below.

• Support bars – The stirrups are held in position by these bars, which are located in the top portion of the beam.
• Main Bar– To reduce shear stresses (shear force).
• Stirrups –Their profile is what defines them in general such as shape, cross-section, length, material. This horizontal element of RCC structures carries the load and protects against bending and shear loads.

Some important Standard sizes of the Beams:

According to the standard, the dimensions (as per IS codes) of a building are 9 x 12 inches each (or 225 x 300 mm). With the addition of slab thickness of 125mm, the minimum size of the beam (specific RCC) manufacturing is 9 x 9 each in inches (or 225x 225mm).

Classification of Beam

In engineering, beams are of several types which are discussed below.

1. Simply supported beam - a beam with no moment resistance that is supported on both ends and is free to spin.
2. Cantilever beam - a projecting beam with just one end attached to the ground.
3. Fixed or Encastre beam - a beam that is supported on both ends and is not rotatable.
4. Overhanging beam - a basic beam with one end that extends beyond its support.
5. Double overhanging beam- A simple beam with both ends extended well beyond supports on both ends is known as a double overhanging.
6. Trussed beam - A truss is a beam that has been strengthened by the insertion of cabling or rods.
7. Continuous beam – a beam that spans many supports.
8. Beam on spring supports,
9. Beam on a flexible or elastic foundation

 The following are the various sorts (difference in characteristics based on their structure)or types of beams that can be represented as different types of beams are utilized to construct a structure based on the design criteria, which are described below. The beams can be distinguished in terms of supports, geometry, cross-section, equilibrium conditions, and material categories. They are further shown in different sub-categories.

Other classifications of Beams are

i) Based on geometry

• Straight beam - e.g. straight profile
• Curved beam – e.g. curved profile
• Tapered beam – e.g. tapered sectional view

ii) Based on the shape of the cross-section

• I-beam –such as ‘I’ cross-section
• T-beam –such as ‘T’ cross-section
• C-beam –such as ‘C’ cross-section

iii) Based on the type of support

• Cantilever beam
• Continuous beam
• Simply supported beam
• Fixed-beam
• Overhanging beam

iv) Based on equilibrium conditions

• Statically determinate beam
• Statically indeterminate beam

Some of the important types

Cantilever Beam

At one end, the cantilever beam is supported, while at the other, it is unsupported. Cantilever beams are commonly used to support a building's canopy or sunshade, which has a greater span. Cantilever beams are designed to withstand the highest moments and shear forces generated at the support section, which is generally a reinforced concrete column.

Fixed Beam

Both ends of the beam are supported, and it resists rotation. On either a wall or a column, both ends of the beam resist.

Simply supported Beam

It is the most basic form of a beam in a framework. It has pinned support on one end and roller support on the other. As a result, the basic beam is supported on both ends but is free to spin.

Overhanging Beam

It's a different kind of beam. Overhanging beams occur when one end of the beam extends beyond the support, while double overhanging beams occur when both ends of the beam extend beyond the support.

Continuous Beam

In multi-story structures with several bays in a perpendicular direction, continuous beams are often employed. There are more than two supports in this sort of beam. One end of the beam is stationary, while the other continues.

Composite Beam

An Encased or Composite beam is a horizontal structural element made up of steel sections and concrete. The composite beam was primarily used in truss structures to prevent steel from corroding due to chemical damage.

L Beam

L- beams are edge beams that are monolithically cast and have slabs on just one side of the rib. At the support sections, the torsional and hogging bending moments are at their highest.

Lintel Beam

The lintel beam is a different sort of beam that is used to support openings such as windows and doors.

In general, a beam is a part that is bent and intended to take the bending moment. A beam is a type of structural component that bends to take vertical loads. There are several sorts of beams based on their material classification such as steel beams, RCC beams (both single and double reinforced), wooden beams, etc.

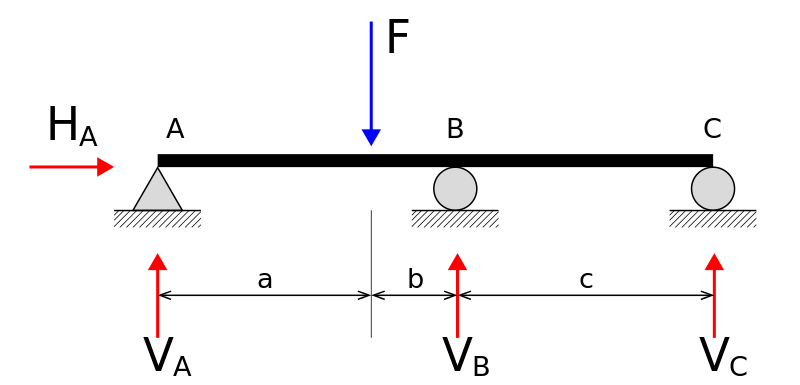
Shear force and Bending moment diagrams

Shear force diagrams (SFD) and bending moment diagrams (BMD) are analytical or superposition methods or techniques that are used in combination with structural analysis to aid structural design or a graphical representation by calculating the value of shear force and bending moment at a particular location of a structural element, such as for a beam. SFD and BMD are computed based on the differential equation in terms of the Euler equation.

For instance, the simply supported beam has some moment with its support reactions then the SFD and BMD can be estimated based on the free-body diagram, shear force diagram and moment diagram view is shown below.

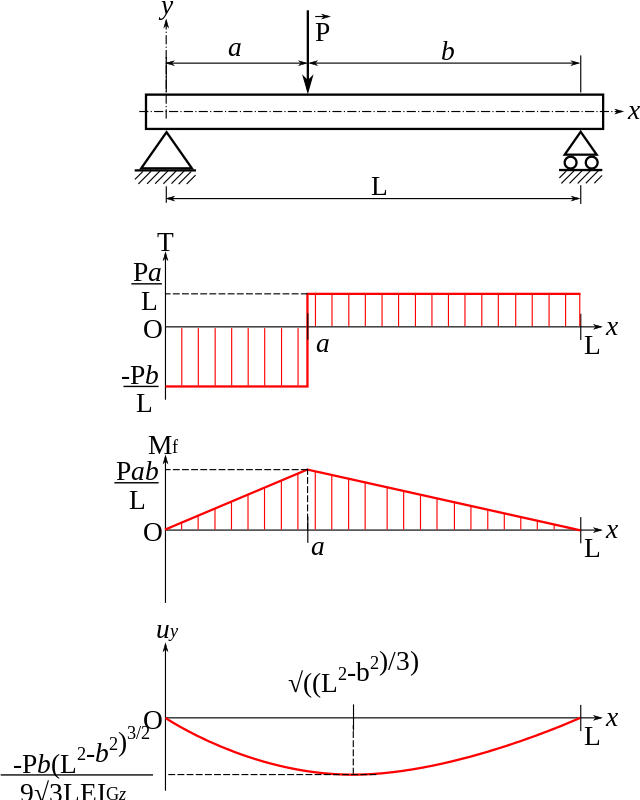
Slope and Beam deflection equations

In general, deflection is computed by dividing moment (M) by EI (Young's modulus x moment of inertia), which is the double integral of the Bending Moment Equation.

Basic Formula to compute slope.

$Slope \left(\theta \right)=\int \frac{M\left(x\right)dx}{EI}$

and deflection is estimated as

$deflection \left(\delta \right)=\theta .x$

whereas x is the centroid of the given section.

Context and Application

Beams are utilized to Bridges, construction beams, and machine tool beds as well as sustain the weight of a building's floors, ceilings, and roofs while also transferring the load to a vertical load-bearing element. all examples beam with point loading in numerical practice.

This topic is useful for the students who are undergoing the following courses:

• Bachelors in Technology (Civil Engineering)
• Masters in Technology (Civil Engineering)
• Bachelor of Science in Physics
• Master of Science in Physics

Practice Problems

1 Which of the following is a type of continuous beams?

1. Statically indeterminate beams
2. Statically determinate beams
3. Statically gravity beams
4. Framed beams

Answer: a

Explanation: Statically indeterminate beams cannot be analyzed only by using static equations such as fixed beams and continuous beams.

2 Identify the name of the beam with carrying increasing and decreasing load from one end to another end is load.

1. Uniformly distributed load
2. Uniformly varying load
3. Uniformly decent load
4. Point load

Answer: b

Explanation: Uniformly varying loads (A load is zero to increase uniformly from one end to the other end.) This type of beam is having a varying load in the whole section.

3 Which of the following is an example of a fixed-beam?

1. Encastered beam
2. Built on beam
3. Rigid beam
4. Tie beam

Answer: a

Explanation: Encastered beam is basically the type of beam where fixed at both supports is called a fixed beam.

4. Which of the following is the beam that has one fixed end and one free end with point load?

1. Cantilever
2. Continuous
3. Overhanging
4. Propped cantilever

Answer: d

Explanation:  Cantilever beam fixed at one end and free at other end and load is pointed at the end of the free end or nearer to that free end.

5.  What of the following is the type of beam that extends beyond its supports?

1. Overhung beam
2. Over span beam
3. Isolated beams
4. Tie beams

Answer: a

Explanation: over hung portion. The beam extended beyond its support in which the extra load is carried beyond the supports comes under this type of beam.

Formulas

• SFD and BMD slope calculation concept

$Slope \left(\theta \right)=\int \frac{M\left(x\right)dx}{EI}$

• SFD and BMD deflection calculation 

$deflection \left(\delta \right)=\theta .x$

Related concepts

• Beam classification is based on different criteria.
• SFD concept
• BMD concept
• SFD and BMD slope calculation concept
• SFD and BMD deflection calculation concept