
Concept explainers
Ten mL of pure liquid water in a cylinder with a movable piston is heated at a constant pressure of 1 atm from an initial temperature of 80°C. The temperature of the system is monitored, and the following behavior is observed:
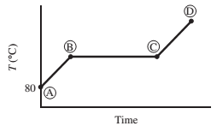
(a) What is happening in steps AB, BC, and CD? What is the temperature corresponding to the horizontal portion of the curve?
(b) Estimate the volume occupied by the water at points B and C. (Assume the vapor follows the ideal-gas equation of state.)
(a)
Interpretation:
Identify the process in AB, BC, CD areas and calculate horizontal zone temperature.
Concept introduction:
Energy is transferred into a system when it is heated. The system will change depending on the energy it receives. This can happen through increase in temperature. A heating curve is called a plot of the temperature versus time.
Answer to Problem 6.1P
- AB − Water liquid heating zone (temperature increase)
- BC − Vaporization of water (liquid to gas phase)
- CD − water vapor (gas phase) heating zone
Horizontal portion temperature = 100°C
Explanation of Solution
AB Step
As heat is absorbed, the temperature of the liquid begins to increase this is due to the increase in the kinetic energy of the molecules of liquid. For standard atmospheric pressure, the rise in temperature takes place until it reaches to 100°C. With increasing temperature, the volume of the liquid remains constant due to little expansion for liquids.
BC Step
At this point, the heat is consumed to begin vaporization of liquid. This temperature is known as the bubble point temperature. Due to change in the previous state, the temperature remains constant and water molecules are moving from liquid to vapor phase. At point C, the last drop of liquid gets evaporated.
CD Step
The temperature increases above 100 °C, when heating steam boils all the liquid into vapor. This cause increase in the volume. Step B shows transition of liquid to vapor. The boiling point of water is 100 °C (liquid here is water) and pressure is 1 atm.
(b)
Interpretation:
Volume occupied by water at point B and C should be calculated.
Concept introduction:
The ideal gas equation is represented as follows:
Here,
Answer to Problem 6.1P
At point B, the water is present as liquid only thus, the volume will be 10 mL
At point C
Explanation of Solution
At point B, the water is present as liquid only thus, the volume will be 10 mL
The number of moles in 10 mL of liquid water is calculated as follows:
The volume of vapor can be calculated using the ideal gas equation as follows:
Here, number of moles is 0.555 mol at 1 atm and
Putting the values,
Thus, at point C, the volume occupied by the water occupies is 17 L.
At point C,
Want to see more full solutions like this?
Chapter 6 Solutions
ELEM PRIN CHEM PROCESS ETXT + WILEYPLUS
Additional Engineering Textbook Solutions
Electric Circuits. (11th Edition)
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
Java: An Introduction to Problem Solving and Programming (8th Edition)
Mechanics of Materials (10th Edition)
Starting Out with Python (4th Edition)
- Can you provide me the answer of these pleasearrow_forwardA constant-volume process involving 2.0 moles of diatomic ideal gas, for which cV = (5/2)R, is at an initial state of 111 kPa and 277 K and is then heated reversibly to 356 K. Calculate the P2 (kPa), dU (kJ), heat transfer q (kJ mol–1), and w (kJ mol–1).arrow_forwardProblem 1 Marks: 60 Section: 1a): 30 marks, Section 1b):30 marks A laboratory scale fluidized bed is considered for studying a catalytic ozone decomposition. a) It is requested to derive model equations under the following assumptions: ■ Operation of the catalytic reactor under steady state conditions, There is no influence of thermal ozone decomposition reactions. The fluidized bed includes bubbles and dense phase. □ The dense phase can be simulated using a CSTR The fluidized bed bubbles contain catalyst particles and can be simulated as a DSTR (batch). □ The jets contain particles and can be simulated with a PFR. The influence of the freeboard has to be considered using a PFR model. The available catalytic reaction rate model is r (moles/gcat.s)= -k CA b) Same than on a) under unsteady state conditions, using an absorbable and reactive tracer. Note: A step-by step derivation of the model equations is required here. A quick answer will not do. Problem 2 Marks: 40 Section 2a: 30 marks,…arrow_forward
- Penicillin process Penicillium chrysogenum is used to produce penicillin in a 90,000-litre fermenter. The volumetric rate of oxygen uptake by the cells ranges from 0.45 to 0.85 mmol l^−1 min^−1 depending on time during the culture. Power input by stirring is 2.9 W l^−1. Estimate the cooling requirements.arrow_forwardProduction of bakers’ yeast Bakers’ yeast is produced in a 50,000-litre fermenter under aerobic conditions. The carbon substrate is sucrose; ammonia is provided as the nitrogen source. The average biomass composition is CH_1.83O_0.55N_0.17 with 5% ash. Under conditions supporting efficient growth, biomass is the only major product and the biomass yield from sucrose is 0.5 g g^−1. If the specific growth rate is 0.45 h^−1, estimate the rate of heat removal required to maintain constant temperature in the fermenter when the yeast concentration is 10 g l^−1.arrow_forwardSensible energy change Calculate the enthalpy change associated with the following processes:(a) m-Cresol is heated from 25°C to 100°C(b) Ethylene glycol is cooled from 20°C to 10°C(c) Succinic acid is heated from 15°C to 120°C(d) Air is cooled from 150°C to 65°Carrow_forward
- ▼ Enzyme conversion An immobilised enzyme process is used in an ice-cream factory to hydrolyse lactose (C12H22O11) to glucose (C6H12O6) and galactose (C6H1206): C12H22O11 + H2O →→ C6H12O + C6H12O6 Gel beads containing ß-galactosidase are packed into a column reactor; 2500 kg of lactose enters the reactor per day as a 10% solution in water at 25°C. The reactor operates at steady state and 32°C; all of the lactose is converted. Because the heat of reaction for enzyme conversions is not as great as for cell culture, sensible heat changes and heats of mixing cannot be ignored. Lactose Water Ah (kJ gmol¹) C, (cal g¹ ºC-¹) Ahm (kcal gmol¹) 3.7 -5652.5 0.30 1.0 Glucose -2805.0 0.30 5.6 Galactose -2805.7 0.30 5.6 (a) What is the standard heat of reaction for this enzyme conversion? (b) Estimate the heating or cooling requirements for this process. State explicitly whether heating or cooling is needed.arrow_forwardBacterial production of alginate Azotobacter vinelandii is investigated for production of alginate from sucrose. In a continuous fermenter at 28°C with ammonia as nitrogen source, the yield of alginate was found to be 4 g g^−1 oxygen consumed. It is planned to produce alginate at a rate of 5 kg h^−1. Since the viscosity of alginate in aqueous solution is considerable, energy input due to mixing the broth cannot be neglected. The fermenter is equipped with a flat-blade disc turbine; at a satisfactory mixing speed and air flow rate, the power requirements are estimated at 1.5 kW. Calculate the cooling requirements.arrow_forwardPreheating nutrient medium Steam is used to heat nutrient medium in a continuous-flow process. Saturated steam at 150°C enters a coil on the outside of the heating vessel and is completely condensed. Liquid medium enters the vessel at 15°C and leaves at 44°C. Heat losses from the jacket to the surroundings are estimated as 0.22 kW. If the flow rate of medium is 3250 kg h^−1 and its heat capacity is 0.9 cal g^−1 °C^−1, how much steam is required?arrow_forward
- Q3] Determine the optimal operating conditions (XA, t, and CR) in a mixed flow reactor to maximize the concentration of R (CR) in the effluent, where an aqueous feed A with an initial concentration of CA0-40 mol/m³ enters the reactor, undergoes decomposition, and exits as a mixture containing A, R, and S. K₁ AR, FR = k₁C, k₁ = 0.4 m³/(mol min) SA AS, rs = k₂CA, k₂ = 2(min), CA0 = 40 mol/m³arrow_forwardConsider the parallel decomposition of A of different orders with FR = 1, rs = 2CA and IT = C. Determine the maximum concentration of desired product obtainable in mixed flow reactor and plug flow reactor. (1) R is desired product and CA0 = 2. (2) S is desired product and CA0 = 4. R S Tarrow_forward1. Copper is known to be toxic to fish, and in particular, the free ion Cu²+ species typically shows greatest toxicity. a. Calculate the speciation of Cu(II) for freshwater at a pH value of 8.3 as the hardness increases from 20 (soft) to 100 (moderately hard) to 200 (very hard) mg/L as CaCO3. Assume that the total divalent Cu(II) concentration is 10 µg/L. b. Based on your findings in part (a), do you think it is appropriate to set a single regulatory limit or should it depend on variables such as pH and hardness? Explain your answer.arrow_forward
 Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
 Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The





