Chapter 6, Problem 6.19P

To determine

The equation for the retention curve as a function of time and the plot of the retention data.

Answer to Problem 6.19P

  $R_t=1.8e^{-0.63t}+2.2e^{-0.11t}$

Explanation of Solution

Given:

The below data has been given to plot the graph.

  

Formula used:

  $\mu =\frac{0.693}{t_{1/2}}$

Calculation:

The plot of retention data.

  

  

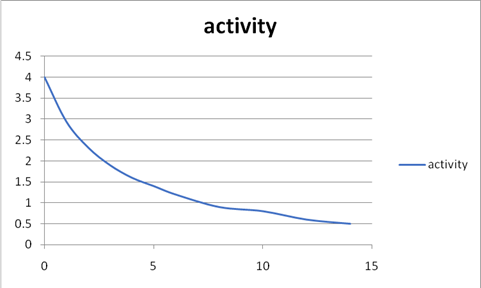
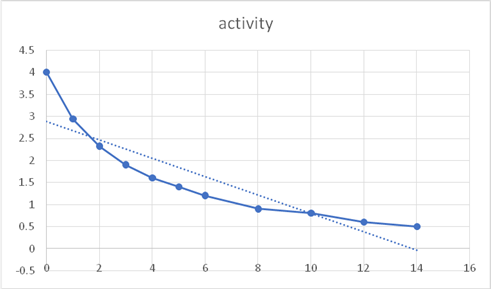
The slope of the line.

  $\begin{array}{l}\mu =\frac{0.693}{t_{1/2}}\\ \mu =\frac{0.693}{65d}\\ \mu =0.11{\text{d}}^{\text{-1}}\\ \\ \text{For}\text{the}\text{long}\text{lived}\text{component}\\ \text{R}\left(t,LL\right)=2.2e^{-0.11t}\\ \text{For}t=0\\ 4\text{MBq}-2.2\text{MBq=1}\text{.8}\text{MBq}\end{array}$

The half-time for this short-lived component is 1.1 days, and the slope is 0.69311.1 days = 0.63 per day. The equation for the short-lived component is:

  $R_t=1.8e^{-0.63t}+2.2e^{-0.11t}$

Day	Total	Long lived	Short lived
0	4	2.2	1.8
1	2.94	1.97	0.97
2	2.32	1.77	0.55
3	1.9	1.58	0.32
4	1.6	1.42	0.18
5	1.4	1.27	0.13

  

Conclusion:

  $R_t=1.8e^{-0.63t}+2.2e^{-0.11t}$

(b)

To determine

The absorbed dose to the patient at day 7 and day 14 after administration of the drug.

Answer to Problem 6.19P

  $D=0.19\text{mGy}$

  $D=0.26\text{mGy}$

Explanation of Solution

Given:

  $\begin{array}{c}\text{Weight of patient}=50kg\\ \stackrel{-}{\text{E}}=0.05\text{MeV}\end{array}$

Formula used:

  $\stackrel{·}{D}=\frac{q\times \stackrel{-}{E\times 1.6\times {10}^{-13}\text{J/MeV}\times 8.64\times {10}^4\text{sec/d}}}{m}$

  $D\text{=}\left[\frac{\left(\text{1}{\text{.38×10}}^{\text{-11}}\text{×1}{\text{.8×10}}^{\text{6}}{\text{Gyd}}^{\text{-1}}\right)}{\text{0}{\text{.63d}}^{\text{-1}}}\text{×}\left({\text{1-e}}^{\text{-0}\text{.63×14}}\right)\right]\text{+}\left[\frac{\left(\text{1}{\text{.38×10}}^{\text{-11}}\text{×2}{\text{.2×10}}^{\text{6}}{\text{Gyd}}^{\text{-1}}\right)}{\text{0}{\text{.11d}}^{\text{-1}}}\text{×}\left({\text{1-e}}^{\text{-0}\text{.11×14}}\right)\right]$

Calculation:

Assumptions: The ¹⁴C to be uniformly distributed throughout the body.

The absorbed dose to the patient at day 7 and day 14 after administration of the drug.

Find dose rate:

  $\begin{array}{l}\stackrel{·}{D}=\frac{\text{q×}\stackrel{\text{-}}{\text{E×1}{\text{.6×10}}^{\text{-13}}\text{J/MeV×8}{\text{.64×10}}^{\text{4}}\text{sec/d}}}{\text{m}}\\ \stackrel{·}{D}=\frac{qBq\times \frac{1\text{trans/sec}}{Bq}\times \stackrel{-}{0.05\text{MeV/trans}\times 1.6\times {10}^{-13}J/\text{MeV}\times 8.64\times {10}^4\text{sec/d}}}{50\text{kg}\frac{\text{1J}}{\text{kg}}\times {\text{Gy}}^{-1}}\\ \stackrel{·}{D}=1.38\times {10}^{-11}q\frac{\text{Gy}}{\text{d/Bq}}\\ D=\frac{{\stackrel{·}{D}}_0}{\lambda }\left(1-e^{-\lambda t}\right)\\ D=\left[\frac{{\stackrel{·}{D}}_1}{{\lambda }_1}\left(1-e^{-{\lambda }_{1}t}\right)\right]+\left[\frac{{\stackrel{·}{D}}_2}{{\lambda }_2}\left(1-e^{-{\lambda }_{2}t}\right)\right]\\ D=\left[\frac{\text{1}{\text{.38×10}}^{\text{-11}}\text{×1}{\text{.8×10}}^{\text{6}}\text{Gy/d}}{\text{0}{\text{.63d}}^{\text{-1}}}\left({\text{1-e}}^{\text{-0}\text{.63×7}}\right)\right]\text{+}\left[\frac{\text{1}{\text{.38×10}}^{\text{-11}}\text{×2}{\text{.2×10}}^{\text{6}}\text{Gy/d}}{\text{0}{\text{.11d}}^{\text{-1}}}\left({\text{1-e}}^{\text{-0}\text{.11×7}}\right)\right]\end{array}$

Absorbed dose to the patient after 7 days.

  $D=0.19\text{mGy}$

Calculating the dose after 14 days in a similar fashion.

  $\begin{array}{l}D=\left[\frac{\left(\text{1}{\text{.38×10}}^{\text{-11}}\text{×1}{\text{.8×10}}^{\text{6}}{\text{Gyd}}^{\text{-1}}\right)}{\text{0}{\text{.63d}}^{\text{-1}}}\text{×}\left({\text{1-e}}^{\text{-0}\text{.63×14}}\right)\right]\text{+}\left[\frac{\left(\text{1}{\text{.38×10}}^{\text{-11}}\text{×2}{\text{.2×10}}^{\text{6}}{\text{Gyd}}^{\text{-1}}\right)}{\text{0}{\text{.11d}}^{\text{-1}}}\text{×}\left({\text{1-e}}^{\text{-0}\text{.11×14}}\right)\right]\\ D=\left[3.94\times {10}^{-5}\left(1-0.00015\right)\right]+\left[27.6\times {10}^{-5}\left(1-0.21\right)\right]\\ D=25.75\times {10}^{-5}\text{Gy}\\ D=25.75\times {10}^{-2}\text{Gy}\\ D=0.26\text{mGy}\end{array}$

Conclusion:

  $D=0.19\text{mGy}$

  $D=0.26\text{mGy}$

(c)

To determine

The dose commitment from the procedure.

Answer to Problem 6.19P

  $D=0.32\text{mGy}$

Explanation of Solution

Given:

  $\begin{array}{l}\stackrel{·}{D_1}=1.38\times {10}^{-11}\times 1.8\times {10}^6{\text{Gyd}}^{\text{-1}}\\ \stackrel{·}{D_2}=1.38\times {10}^{-11}\times 2.2\times {10}^6{\text{Gyd}}^{-1}\\ {\lambda }_1=0.63{\text{d}}^{\text{-1}}\\ {\lambda }_2=0.11{\text{d}}^{\text{-1}}\end{array}$

Formula used:

  $D=\left[\frac{{\stackrel{·}{D}}_1}{{\lambda }_1}\right]+\left[\frac{{\stackrel{·}{D}}_2}{{\lambda }_2}\right]$

Calculation:

  $\begin{array}{l}\text{D=}\left[\frac{\left(\text{1}{\text{.38×10}}^{\text{-11}}\text{×1}{\text{.8×10}}^{\text{6}}{\text{Gyd}}^{\text{-1}}\right)}{\text{0}{\text{.63d}}^{\text{-1}}}\right]\text{+}\left[\frac{\left(\text{1}{\text{.38×10}}^{\text{-11}}\text{×2}{\text{.2×10}}^{\text{6}}{\text{Gyd}}^{\text{-1}}\right)}{\text{0}{\text{.11d}}^{\text{-1}}}\right]\\ D=\left[\frac{\left(\text{2}{\text{.5×10}}^{\text{-5}}{\text{Gyd}}^{\text{-1}}\right)}{\text{0}{\text{.63d}}^{\text{-1}}}\right]\text{+}\left[\frac{\left(\text{3}{\text{.036×10}}^{\text{-5}}{\text{Gyd}}^{\text{-1}}\right)}{\text{0}{\text{.11d}}^{\text{-1}}}\right]\\ D=0.32\text{mGy}\end{array}$

Conclusion:

  $D=0.32\text{mGy}$