Chapter 6, Problem 112AP

All molecules undergo vibrational motions. Quantum mechanical treatment shows that the vibrational energy $E_{\text{vib}}$ of a diatomic molecule such as HCl, give by

$E_{\text{vib}}=\left(n+\frac{1}{2}\right)hv$

Where n is a quantum number $\left(n=0,1,2,3,\mathrm{...}\right)$ and v is the fundamental frequency of vibration. (a) Sketch the first three vibrational energy levels for HCl. (b) Calculate the energy required to excite an HCl molecule from the grond level to the first excited level. The fundamental frequency of virbration for HCl is $8.66\times {10}^{13}{\text{s}}^{\text{-1}}$. (c) The fact that the lowest vibrational energy in the ground level is not zero but equal to $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.hv$ means that molecules will vibrate at all temperatures, including absolute zero. Use the Heisenberg uncertainty principle to justify this prediction. (Hint: Consider a molecule that is not vibrating and start by predicting the uncertainty in its momentum.)

Interpretation Introduction

Interpretation:

The first three vibrational energy levels for $\text{HCl}$

l is to be drawn. The energy required for the transition of molecule from ground state to first excited state is to be determined, and “the reason for lowest vibrational energy in ground state is not zero, but it is equivalent to $\frac{1}{2}\text{h}v$

” is to be justified by using Heisenberg Principle.

Concept introduction:

The energy of a photon can be expressed as follows:

$\text{E}=\frac{\text{hc}}{\lambda }$

Here, E is the energy of photon, $\text{h}$ is Planck’s constant $\left(6.63\times {10}^{-34}\text{ J}\cdot \text{s}\right)$, $\text{c}$ is the speed of light $\left(3.0\times {10}^8\text{ m/s}\right)$, and $\lambda$ is the wavelength.

Heisenberg uncertainty principle explains that the product of uncertainty in position and momentum of particle cannot be less than $\frac{\text{h}}{4\pi }$. It is expressed as follows:

$\Delta x\cdot \Delta p\ge \frac{\text{h}}{4\pi }$

Here, $\Delta x$

denotes uncertainty in position, $\Delta p$

denotes uncertainty in momentum, and $\text{h}$

denotes Planck’s constant $\left(6.63\times {10}^{-34}\text{ J}\cdot \text{s}\right)$.

Answer to Problem 112AP

Solution:

a)

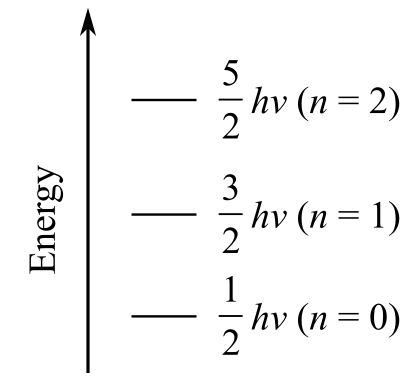
(b) $5.74\times {10}^{-20}\text{ J}$

(c) Consider the diatomic molecule $\text{X}-\text{Y}$ and the distance between them be $x$. If the molecule’s vibrational energy is removed, then the atoms would become stationary with respect to one another and the momentum becomes zero with no uncertainty, that is, $\Delta p$ is zero.

$\begin{array}{l}\Delta x\cdot \Delta p=\frac{\text{h}}{4\pi }\\ \Delta x\cdot 0<\frac{\text{h}}{4\pi }\\ \text{0}<\frac{\text{h}}{4\pi }\end{array}$

This is disallowed by the Heisenberg uncertainty principle.

Explanation of Solution

a) Plot the first three vibrational energy levels for HCl

The vibrational energy of diatomic molecules is given as

$E_{vib}=\left(n+\frac{1}{2}\right)\text{h}v$

The first three vibrational energy levels n are $0,1,\text{ and }2$. Substitute these values in the equation given below to evaluate the vibrational energy for the first three levels

For $n=0$:

$\begin{array}{c}{\left(E_{vib}\right)}_1=\left(n+\frac{1}{2}\right)\text{h}v\\ =\left(0+\frac{1}{2}\right)\text{h}v\\ =\frac{1}{2}\text{h}v\end{array}$

For $n=1$:

$\begin{array}{c}{\left(E_{vib}\right)}_2=\left(1+\frac{1}{2}\right)\text{h}v\\ =\frac{3}{2}\text{h}v\end{array}$

For $n=2$:

$\begin{array}{c}{\left(E_{vib}\right)}_3=\left(2+\frac{1}{2}\right)\text{h}v\\ =\frac{5}{2}\text{h}v\end{array}$

The vibrational energy for the first three energy levels is $\frac{1}{2}\text{h}v$, $\frac{3}{2}\text{h}v$, and $\frac{5}{2}\text{h}v$, respectively. A sketch mentioned below shows the first three vibrational energy levels:

b) The vibrational energy required to excite HCl molecule from ground state to first exited state.

The vibrational energy for the ground state and first excited state are as follows:

$\begin{array}{l}{\left(E_{vib}\right)}_1=\frac{1}{2}\text{h}v\\ {\left(E_{vib}\right)}_2=\frac{3}{2}\text{h}v\end{array}$

For the transition from ground state $\left(n=0\right)$ to first excited state $\left(n=1\right)$, the required transition energy can be can be evaluated as follows:

$\begin{array}{c}\Delta E={\left(E_{vib}\right)}_2-{\left(E_{vib}\right)}_1\\ =\frac{3}{2}\text{h}v-\frac{1}{2}\text{h}v\\ =\text{h}v\end{array}$

Now, substitute the value $6.63\times {10}^{-34}\text{ J}\cdot \text{s}$ for $\text{h}$

and $8.66\times {10}^{13}{\text{ s}}^{-1}$ for $\nu$

in the above equation

$\begin{array}{c}\Delta E=\text{h}v\\ =\left(6.63\times {10}^{-34}\text{ J}\cdot \text{s}\right)\left(8.66\times {10}^{13}{\text{ s}}^{-1}\right)\\ =5.74\times {10}^{-20}\text{ J}\end{array}$.

c) Justify the prediction “that the lowest vibrational energy in the ground state is not zero, but it is equivalent to $\frac{1}{2}\text{h}v$.”

Consider the diatomic molecule $\text{X}-\text{Y}$ and the distance between them be $x$. If the molecule’s vibrational energy is removed, then the atoms would become stationary with respect to one another and hence, the momentum becomes zero with no uncertainty, that is, $\Delta p$ is zero.

As the two atoms are bonded to each other, the uncertainty in position, that is, $\Delta x$ is finite.

Thus,

$\begin{array}{l}\Delta x\cdot \Delta p=\frac{\text{h}}{4\pi }\\ \Delta x\cdot 0<\frac{\text{h}}{4\pi }\\ \text{0}<\frac{\text{h}}{4\pi }\end{array}$

So, this is disallowed by the Heisenberg uncertainty principle.