Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
14th Edition
ISBN: 9780134668574
Author: Raymond A. Barnett, Michael R. Ziegler, Karl E. Byleen, Christopher J. Stocker
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.3, Problem 58E
Problems 51–58 refer to the following slope fields:
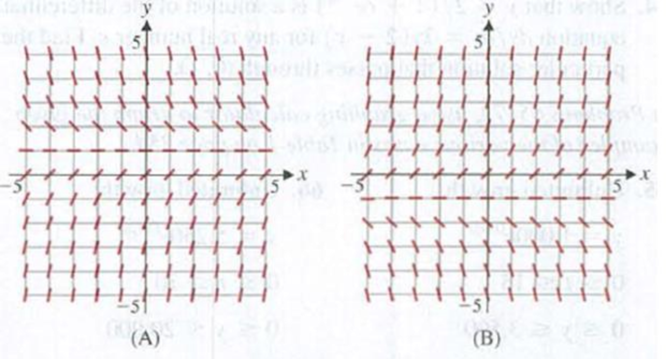
Figure for 51–58
58. Use a graphing calculator to graph y = Cex − 1 for C = −2. −1, 1. and 2, for −5 ≤ x ≤ 5, −5 ≤ y ≤ 5, all in the same viewing window. Observe how the solution curves go with the flow of the tangent line segments in the corresponding slope field shown in Figure A or Figure B.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
(4) (8 points)
(a) (2 points) Write down a normal vector n for the plane P given by the equation
x+2y+z+4=0.
(b) (4 points) Find two vectors v, w in the plane P that are not parallel.
(c) (2 points) Using your answers to part (b), write down a parametrization r: R² —
R3 of the plane P.
(2) (8 points) Determine normal vectors for the planes given by the equations x-y+2z = 3
and 2x + z = 3. Then determine a parametrization of the intersection line of the two
planes.
(3) (6 points)
(a) (4 points) Find all vectors u in the yz-plane that have magnitude [u
also are at a 45° angle with the vector j = (0, 1,0).
= 1 and
(b) (2 points) Using the vector u from part (a) that is counterclockwise to j, find an
equation of the plane through (0,0,0) that has u as its normal.
Chapter 5 Solutions
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Ch. 5.1 - Matched Problem 1 Note that ddx(x3)=3x2 A. Find...Ch. 5.1 - Find each indefinite integral: (A) 2dx (B) 16etdt...Ch. 5.1 - Matched Problem 3 Find each indefinite integral:...Ch. 5.1 - Matched Problem 4 Find the equation of the curve...Ch. 5.1 - Matched Problem 5 Find the revenue function R(x)...Ch. 5.1 - Matched Problem 6 There are currently 64,000...Ch. 5.1 - Explore and Discuss 1 Formulas 1, 2, and 3 do not...Ch. 5.1 - In Problems 18, write each function as a sum of...Ch. 5.1 - In Problems 18, write each function as a sum of...Ch. 5.1 - In Problems 18, write each function as a sum of...
Ch. 5.1 - In Problems 18, write each function as a sum of...Ch. 5.1 - In Problems 18, write each function as a sum of...Ch. 5.1 - Prob. 6ECh. 5.1 - In Problems 18, write each function as a sum of...Ch. 5.1 - Prob. 8ECh. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - In Problems 924, find each indefinite integral....Ch. 5.1 - Is F(x) = (x + 1) (x + 2) an antiderivative of...Ch. 5.1 - Prob. 26ECh. 5.1 - Is F(x) = 1 + x ln x an antiderivative of f(x) = 1...Ch. 5.1 - Is F(x) = x ln x x + e an antiderivative of f(x)...Ch. 5.1 - Is F(x)=(2x+1)33 an antiderivative of f(x) = (2x +...Ch. 5.1 - Is F(x)=(3x2)44 an antiderivative of f(x) = (3x ...Ch. 5.1 - Is F(x)=ex33an antiderivative of f(x)=ex2?...Ch. 5.1 - Is F(x) = (ex 10) (ex + 10) an antiderivative of...Ch. 5.1 - In Problems 3338, discuss the validity of each...Ch. 5.1 - In Problems 3338, discuss the validity of each...Ch. 5.1 - In Problems 3338, discuss the validity of each...Ch. 5.1 - Prob. 36ECh. 5.1 - In Problems 3338, discuss the validity of each...Ch. 5.1 - In Problems 3338, discuss the validity of each...Ch. 5.1 - In Problems 3942, could the three graphs in each...Ch. 5.1 - In Problems 3942, could the three graphs in each...Ch. 5.1 - In Problems 39-42, could the three graphs in each...Ch. 5.1 - In Problems 39-42, could the three graphs in each...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 4354, find each indefinite integral...Ch. 5.1 - In Problems 5562, find the particular...Ch. 5.1 - In Problems 5562, find the particular...Ch. 5.1 - In Problems 5562, find the particular...Ch. 5.1 - In Problems 5562, find the particular...Ch. 5.1 - In Problems 5562, find the particular...Ch. 5.1 - In Problems 5562, find the particular...Ch. 5.1 - In Problems 55-62, find the particular...Ch. 5.1 - In Problems 55-62, find the particular...Ch. 5.1 - Find the equation of the curve that passes through...Ch. 5.1 - Find the equation of the curve that passes through...Ch. 5.1 - In Problems 65-70, find each indefinite integral....Ch. 5.1 - In Problems 6570, find each indefinite integral....Ch. 5.1 - In Problems 6570, find each indefinite integral....Ch. 5.1 - In Problems 6570, find each indefinite integral....Ch. 5.1 - In Problems 6570, find each indefinite integral....Ch. 5.1 - In Problems 6570, find each indefinite integral....Ch. 5.1 - In Problems 7174, find the derivative or...Ch. 5.1 - In Problems 7174, find the derivative or...Ch. 5.1 - In Problems 7174, find the derivative or...Ch. 5.1 - Prob. 74ECh. 5.1 - In Problems 7174, find the derivative or...Ch. 5.1 - Use differentiation to justify the formula...Ch. 5.1 - Assuming that x 0, use differentiation to justify...Ch. 5.1 - Assuming that x 0, use differentiation to justify...Ch. 5.1 - Show that the indefinite integral of the sum of...Ch. 5.1 - Prob. 80ECh. 5.1 - Cost function. The marginal average cost of...Ch. 5.1 - Renewable energy. In 2016, U.S. consumption of...Ch. 5.1 - Production costs. The graph of the marginal cost...Ch. 5.1 - Revenue. The graph of the marginal revenue...Ch. 5.1 - Soles analysis. Monthly sales of an SUV model are...Ch. 5.1 - Sales analysis. The rate of change of the monthly...Ch. 5.1 - Soles analysis. Repeat Problem 85 if S(t)=24t1/370...Ch. 5.1 - 88. Sales analysis. Repeat Problem 86 if S'(t) =...Ch. 5.1 - Labor costs. A defense contractor is starting...Ch. 5.1 - Labor costs. If the rate of labor use in Problem...Ch. 5.1 - Weightheight. For an average person, the rate of...Ch. 5.1 - Prob. 92ECh. 5.1 - Urban growth. The rate of growth of the population...Ch. 5.1 - Learning. A college language class was chosen for...Ch. 5.2 - Find each indefinite integral. (A)(2x33)20(6x2)dx...Ch. 5.2 - Matched Problem 2 (A) Find dy for y = f(x) = x3....Ch. 5.2 - Matched Problem 3 Find (x23x+7)4(2x3)dx by...Ch. 5.2 - Matched Problem 4 Use a substitution to find each...Ch. 5.2 - Matched Problem 5 Integrate. (A)e3xdx (B)xx29dx...Ch. 5.2 - Matched Problem 6 Find xx+1dx.Ch. 5.2 - Prob. 7MPCh. 5.2 - Skills Warm-up Exercises In Problems 18, use the...Ch. 5.2 - Skills Warm-up Exercises In Problems 1-8, use the...Ch. 5.2 - Skills Warm-up Exercises In Problems 1-8, use the...Ch. 5.2 - Prob. 4ECh. 5.2 - Skills Warm-up Exercises In Problems 18, use the...Ch. 5.2 - Skills Warm-up Exercises In Problems 18, use the...Ch. 5.2 - Skills Warm-up Exercises In Problems 18, use the...Ch. 5.2 - Skills Warm-up Exercises In Problems 18, use the...Ch. 5.2 - Prob. 9ECh. 5.2 - In Problems 9-44, find each indefinite integral...Ch. 5.2 - In Problems 9-44, find each indefinite integral...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - Prob. 28ECh. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - Prob. 35ECh. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 944, find each indefinite integral and...Ch. 5.2 - In Problems 4550, the indefinite integral can be...Ch. 5.2 - In Problems 4550, the indefinite integral can be...Ch. 5.2 - In Problems 4550, the indefinite integral can be...Ch. 5.2 - In Problems 4550, the indefinite integral can be...Ch. 5.2 - In Problems 4550, the indefinite integral can be...Ch. 5.2 - In Problems 4550, the indefinite integral can be...Ch. 5.2 - Is F(x) = x2ex an antiderivative of f(x) = 2xex?...Ch. 5.2 - Is F(x)=1x an antiderivative of f(x) = ln x?...Ch. 5.2 - Is F(x) = (x2 + 4)6 an antiderivative of f(x) =...Ch. 5.2 - Is F(x) = (x2 1)100 an antiderivative of f(x) =...Ch. 5.2 - Is F(x) = e2x + 4 an antiderivative of f(x) = e2x?...Ch. 5.2 - Is F(x) = 1 0.2e5x an antiderivative of f(x) =...Ch. 5.2 - Is F(x) = 0.5(ln x)2 + 10 an antiderivative of...Ch. 5.2 - Prob. 58ECh. 5.2 - C In Problems 5970, find each indefinite integral...Ch. 5.2 - C In Problems 5970, find each indefinite integral...Ch. 5.2 - C In Problems 5970, find each indefinite integral...Ch. 5.2 - C In Problems 5970, find each indefinite integral...Ch. 5.2 - C In Problems 5970, find each indefinite integral...Ch. 5.2 - Prob. 64ECh. 5.2 - C In Problems 5970, find each indefinite integral...Ch. 5.2 - C In Problems 5970, find each indefinite integral...Ch. 5.2 - C In Problems 5970, find each indefinite integral...Ch. 5.2 - C In Problems 5970, find each indefinite integral...Ch. 5.2 - C In Problems 5970, find each indefinite integral...Ch. 5.2 - C In Problems 5970, find each indefinite integral...Ch. 5.2 - Prob. 71ECh. 5.2 - In Problems 7176, find the family of all...Ch. 5.2 - In Problems 7176, find the family of all...Ch. 5.2 - Prob. 74ECh. 5.2 - In Problems 7176, find the family of all...Ch. 5.2 - Prob. 76ECh. 5.2 - Pricedemand equation. The marginal price for a...Ch. 5.2 - Pricesupply equation. The marginal price at a...Ch. 5.2 - Cost function. The weekly marginal cost of...Ch. 5.2 - Revenue function. The weekly marginal revenue from...Ch. 5.2 - Marketing. An automobile company is ready to...Ch. 5.2 - Marketing. Repeat Problem 81 if the monthly rate...Ch. 5.2 - Oil production. Using production and geological...Ch. 5.2 - Oil production. Assume that the rate in Problem 83...Ch. 5.2 - Biology. A yeast culture is growing at the rate of...Ch. 5.2 - Medicine. The rate of healing for a skin wound (in...Ch. 5.2 - Prob. 87ECh. 5.2 - Pollution. An oil tanker aground on a reef is...Ch. 5.2 - Learning. An average student enrolled in an...Ch. 5.2 - Learning. An average student enrolled in a...Ch. 5.2 - College enrollment. The projected rate of increase...Ch. 5.3 - Matched Problem 1 Assuming the same continuous...Ch. 5.3 - Matched Problem 2 If the exponential growth law...Ch. 5.3 - Matched Problem 3 Estimate the age of the bone in...Ch. 5.3 - Matched Problem 4 In Example 4, what is the rate...Ch. 5.3 - Prob. 1EDCh. 5.3 - In Problems 18, express the relationship between...Ch. 5.3 - In Problems 18, express the relationship between...Ch. 5.3 - In Problems 18, express the relationship between...Ch. 5.3 - Prob. 4ECh. 5.3 - In Problems 18, express the relationship between...Ch. 5.3 - In Problems 18, express the relationship between...Ch. 5.3 - In Problems 18, express the relationship between...Ch. 5.3 - In Problems 18, express the relationship between...Ch. 5.3 - A In Problems 920, find the general or particular...Ch. 5.3 - Prob. 10ECh. 5.3 - A In Problems 920, find the general or particular...Ch. 5.3 - A In Problems 920, find the general or particular...Ch. 5.3 - A In Problems 920, find the general or particular...Ch. 5.3 - A In Problems 920, find the general or particular...Ch. 5.3 - A In Problems 920, find the general or particular...Ch. 5.3 - A In Problems 920, find the general or particular...Ch. 5.3 - A In Problems 920, find the general or particular...Ch. 5.3 - Prob. 18ECh. 5.3 - A In Problems 920, find the general or particular...Ch. 5.3 - Prob. 20ECh. 5.3 - In Problems 2124, give the order (first, second,...Ch. 5.3 - Prob. 22ECh. 5.3 - In Problems 2124, give the order (first, second,...Ch. 5.3 - Prob. 24ECh. 5.3 - In Problems 2124, give the order (first, second,...Ch. 5.3 - In Problems 2124, give the order (first, second,...Ch. 5.3 - Is y=9+x2 a solution of the differential equation...Ch. 5.3 - Is y=5ex2/2 a solution of the differential...Ch. 5.3 - Is y = e3x a solution of the differential equation...Ch. 5.3 - Prob. 30ECh. 5.3 - Is y= 100e3x a solution of the differential...Ch. 5.3 - Prob. 32ECh. 5.3 - B Problems 3338 refer to the following slope...Ch. 5.3 - B Problems 3338 refer to the following slope...Ch. 5.3 - B Problems 3338 refer to the following slope...Ch. 5.3 - Prob. 36ECh. 5.3 - B Problems 3338 refer to the following slope...Ch. 5.3 - Prob. 38ECh. 5.3 - In Problems 3946, find the general or particular...Ch. 5.3 - In Problems 3946, find the general or particular...Ch. 5.3 - In Problems 3946, find the general or particular...Ch. 5.3 - In Problems 3946, find the general or particular...Ch. 5.3 - In Problems 3946, find the general or particular...Ch. 5.3 - In Problems 3946, find the general or particular...Ch. 5.3 - In Problems 3946, find the general or particular...Ch. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - Prob. 48ECh. 5.3 - Prob. 49ECh. 5.3 - In Problems 4750, does the given differential...Ch. 5.3 - Problems 5158 refer to the following slope fields:...Ch. 5.3 - Prob. 52ECh. 5.3 - Problems 5158 refer to the following slope fields:...Ch. 5.3 - Problems 5158 refer to the following slope fields:...Ch. 5.3 - Problems 5158 refer to the following slope fields:...Ch. 5.3 - Prob. 56ECh. 5.3 - Problems 5158 refer to the following slope fields:...Ch. 5.3 - Problems 5158 refer to the following slope fields:...Ch. 5.3 - Show that y=Cx2 is a solution of the differential...Ch. 5.3 - Show that y=x2+C is a solution of the differential...Ch. 5.3 - Show that y = Cx is a solution of the differential...Ch. 5.3 - Show that y = C/x is a solution of the...Ch. 5.3 - Show that y = 1/(1 + cet) is a solution of the...Ch. 5.3 - Prob. 64ECh. 5.3 - Prob. 65ECh. 5.3 - Problems 6572, use a graphing calculator to graph...Ch. 5.3 - Prob. 67ECh. 5.3 - Prob. 68ECh. 5.3 - Problems 6572, use a graphing calculator to graph...Ch. 5.3 - Problems 6572, use a graphing calculator to graph...Ch. 5.3 - Problems 6572, use a graphing calculator to graph...Ch. 5.3 - Prob. 72ECh. 5.3 - Show that the rate of logistic growth, dy/dt =...Ch. 5.3 - Find the value of t for which the logistic...Ch. 5.3 - Prob. 75ECh. 5.3 - Prob. 76ECh. 5.3 - Continuous compound interest. Find the amount A in...Ch. 5.3 - Prob. 78ECh. 5.3 - Continuous compound interest. Find the amount A in...Ch. 5.3 - Continuous compound interest. Find the amount A in...Ch. 5.3 - Pricedemand. The marginal price dp/dx at x units...Ch. 5.3 - Pricesupply. The marginal price dp/dx at x units...Ch. 5.3 - Advertising. A company is trying to expose a new...Ch. 5.3 - Prob. 84ECh. 5.3 - Biology. For relatively clear bodies of water, the...Ch. 5.3 - Blood pressure. Under certain assumptions, the...Ch. 5.3 - Drug concentration. A single injection of a drug...Ch. 5.3 - Simple epidemic. A community of 10,000 people is...Ch. 5.3 - Prob. 89ECh. 5.3 - Prob. 90ECh. 5.3 - Archaeology. A skull found in an ancient tomb has...Ch. 5.3 - Learning. For a person learning to type, the...Ch. 5.3 - Prob. 93ECh. 5.3 - Perception. The WeberFechner law concerns a...Ch. 5.3 - Prob. 95ECh. 5.3 - Prob. 96ECh. 5.4 - Prob. 1MPCh. 5.4 - Matched Problem 2 Consider the function f(x) = x2 ...Ch. 5.4 - Matched Problem 3 Referring to the figure for...Ch. 5.4 - Matched Problem 4 Using the same integral values...Ch. 5.4 - Prob. 1EDCh. 5.4 - Explore and Discuss 2 If f(x) in Figure 3 were...Ch. 5.4 - In Problems 16, perform a mental calculation to...Ch. 5.4 - In Problems 16, perform a mental calculation to...Ch. 5.4 - In Problems 16, perform a mental calculation to...Ch. 5.4 - Prob. 4ECh. 5.4 - In Problems 16, perform a mental calculation to...Ch. 5.4 - In Problems 16, perform a mental calculation to...Ch. 5.4 - A Problems 710 refer to the rectangles A, B, C, D,...Ch. 5.4 - A Problems 710 refer to the rectangles A, B, C, D,...Ch. 5.4 - A Problems 710 refer to the rectangles A, B, C, D,...Ch. 5.4 - A Problems 710 refer to the rectangles A, B, C, D,...Ch. 5.4 - Prob. 11ECh. 5.4 - Problems 11-14 refer to the rectangles F, G, H, I,...Ch. 5.4 - Prob. 13ECh. 5.4 - Problems 1114 refer to the rectangles F, G, H, I,...Ch. 5.4 - Problems 1522 involve estimating the area under...Ch. 5.4 - Problems 1522 involve estimating the area under...Ch. 5.4 - Problems 1522 involve estimating the area under...Ch. 5.4 - Problems 1522 involve estimating the area under...Ch. 5.4 - Problems 1522 involve estimating the area under...Ch. 5.4 - Problems 1522 involve estimating the area under...Ch. 5.4 - Problems 1522 involve estimating the area under...Ch. 5.4 - Prob. 22ECh. 5.4 - In Problems 2326, calculate the indicated Riemann...Ch. 5.4 - In Problems 2326, calculate the indicated Riemann...Ch. 5.4 - In Problems 2326, calculate the indicated Riemann...Ch. 5.4 - In Problems 2326, calculate the indicated Riemann...Ch. 5.4 - In Problems 2730, calculate the indicated Riemann...Ch. 5.4 - In Problems 2730, calculate the indicated Riemann...Ch. 5.4 - In Problems 2730, calculate the indicated Riemann...Ch. 5.4 - In Problems 2730, calculate the indicated Riemann...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 3142, calculate the definite integral...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - In Problems 4354, calculate the definite integral,...Ch. 5.4 - B In Problems 5560, discuss the validity of each...Ch. 5.4 - B In Problems 5560, discuss the validity of each...Ch. 5.4 - B In Problems 5560, discuss the validity of each...Ch. 5.4 - Prob. 58ECh. 5.4 - Prob. 59ECh. 5.4 - B In Problems 5560, discuss the validity of each...Ch. 5.4 - Problems 61 and 62 refer to the following figure...Ch. 5.4 - Prob. 62ECh. 5.4 - C Problems 63 and 64 refer to the following...Ch. 5.4 - C Problems 63 and 64 refer to the following...Ch. 5.4 - Prob. 65ECh. 5.4 - Prob. 66ECh. 5.4 - For Problems 6568, use derivatives to determine...Ch. 5.4 - For Problems 6568, use derivatives to determine...Ch. 5.4 - In Problems 6972, the left sum Ln or the right sum...Ch. 5.4 - In Problems 6972, the left sum Ln or the right sum...Ch. 5.4 - In Problems 6972, the left sum Ln or the right sum...Ch. 5.4 - In Problems 6972, the left sum Ln or the right sum...Ch. 5.4 - Prob. 73ECh. 5.4 - Prob. 74ECh. 5.4 - Medicine. The rate of healing, A(t) (in square...Ch. 5.4 - Prob. 76ECh. 5.4 - Learning. A psychologist found that, on average,...Ch. 5.4 - Prob. 78ECh. 5.5 - Matched Problem 1 Repeat Example 1 for the daily...Ch. 5.5 - Matched Problem 2 Evaluated 13(4x2ex+5x)dx.Ch. 5.5 - Matched Problem 3 Use both methods described in...Ch. 5.5 - Matched Problem 4 Use both method 2 described in...Ch. 5.5 - Matched Problem 5 Repeat Example 5 if...Ch. 5.5 - Matched Problem 6 Repeat Example 6 if C(t) = 1 and...Ch. 5.5 - c 1.54.3xlnxdx to three decimal places.Ch. 5.5 - Matched Problem 8 Find the average value of g(t) =...Ch. 5.5 - Matched Problem 9 Given the supply equation...Ch. 5.5 - Prob. 1EDCh. 5.5 - In Problems 18, use geometric formulas to find the...Ch. 5.5 - In Problems 18, use geometric formulas to find the...Ch. 5.5 - In Problems 18, use geometric formulas to find the...Ch. 5.5 - In Problems 18, use geometric formulas to find the...Ch. 5.5 - In Problems 18, use geometric formulas to find the...Ch. 5.5 - In Problems 18, use geometric formulas to find the...Ch. 5.5 - In Problems 18, use geometric formulas to find the...Ch. 5.5 - In Problems 18, use geometric formulas to find the...Ch. 5.5 - A In Problems 912, (A) Calculate the change in...Ch. 5.5 - A In Problems 912, (A) Calculate the change in...Ch. 5.5 - Prob. 11ECh. 5.5 - A In Problems 912, (A) Calculate the change in...Ch. 5.5 - Evaluate the integrals in Problems 1332. 13. 057dxCh. 5.5 - Evaluate the integrals in Problems 1332. 14....Ch. 5.5 - Evaluate the integrals in Problems 1332. 15....Ch. 5.5 - Evaluate the integrals in Problems 1332. 16. 035dxCh. 5.5 - Evaluate the integrals in Problems 1332. 17....Ch. 5.5 - Prob. 18ECh. 5.5 - Evaluate the integrals in Problems 1332. 19....Ch. 5.5 - Evaluate the integrals in Problems 1332. 20....Ch. 5.5 - Evaluate the integrals in Problems 1332. 21....Ch. 5.5 - Prob. 22ECh. 5.5 - Evaluate the integrals in Problems 1332. 23....Ch. 5.5 - Evaluate the integrals in Problems 1332. 24....Ch. 5.5 - Evaluate the integrals in Problems 1332. 25....Ch. 5.5 - Prob. 26ECh. 5.5 - Evaluate the integrals in Problems 1332. 27....Ch. 5.5 - Evaluate the integrals in Problems 1332. 28....Ch. 5.5 - Evaluate the integrals in Problems 1332. 29....Ch. 5.5 - Evaluate the integrals in Problems 1332. 30....Ch. 5.5 - Evaluate the integrals in Problems 1332. 31....Ch. 5.5 - Evaluate the integrals in Problems 1332. 32....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 33....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 34....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 35....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 36....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 37....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 38....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 39....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 40....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 41....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 42....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 43....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 44....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 45....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 46....Ch. 5.5 - B Evaluate the integrals in Problems 3348. 47....Ch. 5.5 - Prob. 48ECh. 5.5 - In Problems 4956, (A)Find the average value of...Ch. 5.5 - Prob. 50ECh. 5.5 - In Problems 4956, (A)Find the average value of...Ch. 5.5 - In Problems 4956, (A)Find the average value of...Ch. 5.5 - In Problems 4956, (A)Find the average value of...Ch. 5.5 - Prob. 54ECh. 5.5 - In Problems 4956, (A)Find the average value of...Ch. 5.5 - In Problems 4956, (A)Find the average value of...Ch. 5.5 - C Evaluate the integrals in Problems 5762. 57....Ch. 5.5 - C Evaluate the integrals in Problems 5762. 58....Ch. 5.5 - C Evaluate the integrals in Problems 5762. 59....Ch. 5.5 - C Evaluate the integrals in Problems 5762. 60....Ch. 5.5 - C Evaluate the integrals in Problems 5762. 61....Ch. 5.5 - C Evaluate the integrals in Problems 5762. 62....Ch. 5.5 - Prob. 63ECh. 5.5 - Use a numerical integration routine to evaluate...Ch. 5.5 - Use a numerical integration routine to evaluate...Ch. 5.5 - Use a numerical integration routine to evaluate...Ch. 5.5 - The mean value theorem states that if F(x) is a...Ch. 5.5 - Prob. 68ECh. 5.5 - Cost. A company manufactures mountain bikes. The...Ch. 5.5 - Cost. Referring to Problem 69, compute the...Ch. 5.5 - Salvage value. A new piece of industrial equipment...Ch. 5.5 - Maintenance costs. Maintenance costs for an...Ch. 5.5 - 73. Employee training. A company producing...Ch. 5.5 - Prob. 74ECh. 5.5 - Useful life. The total accumulated costs C(t) and...Ch. 5.5 - Useful life. The total accumulated costs C(t) and...Ch. 5.5 - Average cost. The total cost (in dollars) of...Ch. 5.5 - Average cost. The total cost (in dollars) of...Ch. 5.5 - Sales. The rate at which the total number of sales...Ch. 5.5 - Prob. 80ECh. 5.5 - Supply function. Given the supply function...Ch. 5.5 - Demand function. Given the demand function...Ch. 5.5 - Labor costs and learning. A defense contractor is...Ch. 5.5 - Labor costs and learning. If the rate of labor use...Ch. 5.5 - Prob. 85ECh. 5.5 - Repeat Problem 85 with an order of 1.200 units...Ch. 5.5 - Oil production. Using production and geological...Ch. 5.5 - Prob. 88ECh. 5.5 - Biology. A yeast culture weighing 2 grams is...Ch. 5.5 - Medicine. The rate at which the area of a skin...Ch. 5.5 - Temperature. If the temperature in an aquarium (in...Ch. 5.5 - Medicine. A drug is injected into the bloodstream...Ch. 5.5 - Politics. Public awareness of a congressional...Ch. 5.5 - Population composition. The number of children in...Ch. 5 - Find each integral in Problems 16. 1. (6x+3)dxCh. 5 - Find each integral in Problems 16. 2. 10205dxCh. 5 - Find each integral in Problems 16. 3. 09(4t2)dtCh. 5 - Prob. 4RECh. 5 - Find each integral in Problems 16. 5. 1+u4uduCh. 5 - Find each integral in Problems 16. 6. 01xe2x2dxCh. 5 - Is F(x) = ln x2 an antiderivative of f(x) = ln...Ch. 5 - Is F(x) = ln x2 an antiderivative of f(x)=2x?...Ch. 5 - Is F(x) = (ln x)2 an antiderivative of f(x) =2 ln...Ch. 5 - Is F(x) = (ln x)2 an antiderivative of f(x)=2lnxx?...Ch. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - In Problems 13 and 14, find the derivative or...Ch. 5 - In Problems 13 and 14, find the derivative or...Ch. 5 - Find a function y = f(x) that satisfies both...Ch. 5 - Find all antiderivatives of (A)dydx=8x34x1...Ch. 5 - Approximate 15(x2+1) dx, using a right sum with n...Ch. 5 - Prob. 18RECh. 5 - Use the following table of values and a left sum...Ch. 5 - Find the average value of f(x) = 6x2 + 2x over the...Ch. 5 - Describe a rectangle that has the same area as the...Ch. 5 - In Problems 22 and 23, calculate the indicated...Ch. 5 - In Problems 22 and 23, calculate the indicated...Ch. 5 - Use the graph and actual areas of the indicated...Ch. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Use the graph and actual areas of the indicated...Ch. 5 - Use the graph and actual areas of the indicated...Ch. 5 - Prob. 29RECh. 5 - Use the graph and actual areas of the indicated...Ch. 5 - Prob. 31RECh. 5 - Problems 3237 refer to the slope field shown in...Ch. 5 - Problems 3237 refer to the slope field shown in...Ch. 5 - Problems 3237 refer to the slope field shown in...Ch. 5 - Prob. 35RECh. 5 - Prob. 36RECh. 5 - Prob. 37RECh. 5 - Find each integral in Problems 3848. 38.111+xdxCh. 5 - Find each integral in Problems 3848....Ch. 5 - Find each integral in Problems 3848. 40.5etdtCh. 5 - Find each integral in Problems 3848. 41.1e1+t2tdtCh. 5 - Find each integral in Problems 3848. 42.xe3x2dxCh. 5 - Find each integral in Problems 3848. 43.3112xdxCh. 5 - Prob. 44RECh. 5 - Find each integral in Problems 3848....Ch. 5 - Prob. 46RECh. 5 - Find each integral in Problems 3848. 47.exex+3dxCh. 5 - Prob. 48RECh. 5 - Find a function y = f(x) that satisfies both...Ch. 5 - Find the equation of the curve that passes through...Ch. 5 - (A)Find the average value off(x)=3x over the...Ch. 5 - Prob. 52RECh. 5 - Find each integral in Problems 5256 53.x(x31)2dxCh. 5 - Prob. 54RECh. 5 - Find each integral in Problems 5256. 55.07x16xdxCh. 5 - Prob. 56RECh. 5 - Find a function y = f(x) that satisfies both...Ch. 5 - Prob. 58RECh. 5 - Graph Problems 5962 on a graphing calculator, and...Ch. 5 - Prob. 60RECh. 5 - Graph Problems 59-62 on a graphing calculator, and...Ch. 5 - Prob. 62RECh. 5 - Prob. 63RECh. 5 - Use a numerical integration routine to evaluate...Ch. 5 - Use a numerical integration routine to evaluate...Ch. 5 - Prob. 66RECh. 5 - Prob. 67RECh. 5 - Prob. 68RECh. 5 - Profit function. If the marginal profit for...Ch. 5 - Prob. 70RECh. 5 - Inventory. Suppose that the inventory of a certain...Ch. 5 - Price-supply. Given the price-supply function...Ch. 5 - Prob. 73RECh. 5 - Prob. 74RECh. 5 - Prob. 75RECh. 5 - Pollution. An environmental protection agency...Ch. 5 - Population. The population of Mexico was 116...Ch. 5 - Archaeology. The continuous compound rate of decay...Ch. 5 - Learning. An average student enrolled in a typing...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Testing Hypotheses. In Exercises 13-24, assume that a simple random sample has been selected and test the given...
Elementary Statistics Using The Ti-83/84 Plus Calculator, Books A La Carte Edition (5th Edition)
For each hour of class time, how many hours outside of class are recommended for studying and doing homework?
Elementary Algebra For College Students (10th Edition)
Complete each statement with the correct term from the column on the right. Some of the choices may not be used...
Intermediate Algebra (13th Edition)
Find E(X) for each of the distributions given in Exercise 2.1-3.
Probability And Statistical Inference (10th Edition)
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
Students in a Listening Responses class bought 40 tickets for a piano concert. The number of tickets purchased ...
Elementary and Intermediate Algebra: Concepts and Applications (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- (1) (4 points) Give a parametrization c: R R³ of the line through the points P = (1,0,-1) and Q = (-2, 0, 1).arrow_forward7. Show that for R sufficiently large, the polynomial P(z) in Example 3, Sec. 5, satisfies the inequality |P(z)| R. Suggestion: Observe that there is a positive number R such that the modulus of each quotient in inequality (9), Sec. 5, is less than |an|/n when |z| > R.arrow_forward9. Establish the identity 1- 1+z+z² + 2n+1 ... +z" = 1- z (z1) and then use it to derive Lagrange's trigonometric identity: 1 1+ cos cos 20 +... + cos no = + 2 sin[(2n+1)0/2] 2 sin(0/2) (0 < 0 < 2л). Suggestion: As for the first identity, write S = 1+z+z² +...+z" and consider the difference S - zS. To derive the second identity, write z = eie in the first one.arrow_forward
- 8. Prove that two nonzero complex numbers z₁ and Z2 have the same moduli if and only if there are complex numbers c₁ and c₂ such that Z₁ = c₁C2 and Z2 = c1c2. Suggestion: Note that (i≤ exp (101+0) exp (01-02) and [see Exercise 2(b)] 2 02 Ꮎ - = = exp(i01) exp(101+0) exp (i 01 - 02 ) = exp(102). i 2 2arrow_forwardnumerical anaarrow_forward13. If X has the distribution function F(x) = 0 1 12 for x < -1 for -1x < 1 for 1x <3 2 3 for 3≤x≤5 4 1 for x≥5 find (a) P(X ≤3); (b) P(X = 3); (c) P(X < 3); (d) P(X≥1); (e) P(-0.4arrow_forwardTwo measurements are made of some quantity. For the first measurement, the average is 74.4528, the RMS error is 6.7441, and the uncertainty of the mean is 0.9264. For the second one, the average is 76.8415, the standard deviation is 8.3348, and the uncertainty of the mean is 1.1448. The expected value is exactly 75. 13. Express the first measurement in public notation. 14. Is there a significant difference between the two measurements? 1 15. How does the first measurement compare with the expected value? 16. How does the second measurement compare with the expected value?arrow_forwardNo chatgpt pls will upvote Already got wrong chatgpt answer .arrow_forwardIf you use any chatgpt will downvote.arrow_forwardPlease help I'm a working mom trying to help my son last minute (6th grader)! Need help with the blank ones and check the ones he got with full calculation so we can use it to study! Especially the mixed number fractions cause I'm rusty. Thanks in advance!arrow_forward|| 38 5층-11- 6 4 7 2 6arrow_forward4. Consider the initial value problem y' = 3x(y-1) 1/3, y(xo) = yo. (a) For what points (co, yo) does the IVP have a solution? (b) For what points (xo, yo) does the IVP have a unique solution on some open interval that contains 20? (c) Solve the IVP y' = 3x(y-1) 1/3, y(0) = 9 and determine the largest open interval on which this solution is unique.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Intro to the Laplace Transform & Three Examples; Author: Dr. Trefor Bazett;https://www.youtube.com/watch?v=KqokoYr_h1A;License: Standard YouTube License, CC-BY