International Edition---engineering Mechanics: Statics, 4th Edition
4th Edition
ISBN: 9781305501607
Author: Andrew Pytel And Jaan Kiusalaas
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5, Problem 5.32P
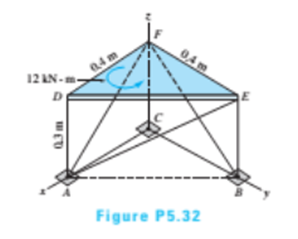
Calculate the reaction at D for the structure described in Prob. 5.11.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
100
As a spring is heated, its spring constant decreases. Suppose the spring is heated and then cooled so that the
spring constant at time t is k(t) = t sin + N/m. If the mass-spring system has mass m = 2 kg and a
damping constant b = 1 N-sec/m with initial conditions x(0) = 6 m and x'(0) = -5 m/sec and it is
subjected to the harmonic external force f (t) = 100 cos 3t N. Find at least the first four nonzero terms in
a power series expansion about t = 0, i.e. Maclaurin series expansion, for the displacement:
• Analytically (hand calculations)
Creating Simulink Model
Plot solutions for first two, three and four non-zero terms as well as the Simulink solution on the same graph
for the first 15 sec. The graph must be fully formatted by code.
Two springs and two masses are attached in a straight vertical line as shown in Figure Q3. The system is set
in motion by holding the mass m₂ at its equilibrium position and pushing the mass m₁ downwards of its
equilibrium position a distance 2 m and then releasing both masses. if m₁ = m² = 1 kg, k₁ = 3 N/m and
k₂ = 2 N/m.
(y₁ = 0)
www
k₁ = 3
Jm₁ = 1
k2=2
www
(Net change in
spring length
=32-31)
(y₂ = 0)
m₂ = 1
32
32
System in
static
equilibrium
System in
motion
Figure Q3 - Coupled mass-spring system
Determine the equations of motion y₁ (t) and y₂(t) for the two masses m₁ and m₂ respectively:
Analytically (hand calculations)
Using MATLAB Numerical Functions (ode45)
Creating Simulink Model
Produce an animation of the system for all solutions for the first minute.
Two large tanks, each holding 100 L of liquid, are interconnected by pipes, with the liquid flowing from tank
A into tank B at a rate of 3 L/min and from B into A at a rate of 1 L/min (see Figure Q1). The liquid inside each
tank is kept well stirred. A brine solution with a concentration of 0.2 kg/L of salt flows into tank A at a rate of
6 L/min. The diluted solution flows out of the system from tank A at 4 L/min and from tank B at 2 L/min. If,
initially, tank A contains pure water and tank B contains 20 kg of salt.
A
6 L/min
0.2 kg/L
x(t)
100 L
4 L/min
x(0) = 0 kg
3 L/min
1 L/min
B
y(t)
100 L
y(0) = 20 kg
2 L/min
Figure Q1 - Mixing problem for interconnected tanks
Determine the mass of salt in each tank at time t≥ 0:
Analytically (hand calculations)
Using MATLAB Numerical Functions (ode45)
Creating Simulink Model
Plot all solutions on the same graph for the first 15 min. The graph must be fully formatted by code.
Chapter 5 Solutions
International Edition---engineering Mechanics: Statics, 4th Edition
Ch. 5 - Bar AB of negligible weight is supported by a...Ch. 5 - Draw the FBD for the bar described in Prob. 5.1 if...Ch. 5 - The space truss ABCD in the shape of a tetrahedron...Ch. 5 - Draw the FBD of the portion BCD of the space truss...Ch. 5 - The homogeneous plate of weight W is supported by...Ch. 5 - The bar ABCD of negligible weight is supported by...Ch. 5 - The shaft-pulley assembly is supported by the...Ch. 5 - The 60-lb homogeneous door is supported by hinges...Ch. 5 - Draw the FBD for bar BCD. The connections at A and...Ch. 5 - The homogeneous 360-lb plate with a rectangular...
Ch. 5 - The L-shaped rod, supported by slider bearings at...Ch. 5 - The homogeneous 240-lb bar is supported by a rough...Ch. 5 - In Sample Problem 5.4, determine the tension TAC...Ch. 5 - In Sample Problem 5.5, compute the tension TAD...Ch. 5 - In Sample Problem 5.5, determine Oy with one...Ch. 5 - Determine the tension TB in Sample Problem 5.6...Ch. 5 - Compute the tension TAE in Sample Problem 5.7...Ch. 5 - The 80-lb homogeneous plate is suspended from four...Ch. 5 - The three bars are welded together to form a rigid...Ch. 5 - The compound bar is supported by a thrust bearing...Ch. 5 - The homogeneous 20-kg door is held in the...Ch. 5 - The light boom AB is attached to the vertical wall...Ch. 5 - The homogeneous 80-kg sign is suspended from a...Ch. 5 - The bar ABC is supported by a ball-and-socket at A...Ch. 5 - Determine the forces in members PAE,PAF, and PBG...Ch. 5 - The figure shows the FBD of a portion of the space...Ch. 5 - Calculate all forces acting on the bar AB...Ch. 5 - Determine the forces in members AD, BD, and CD of...Ch. 5 - Find the tension in cable BE that supports the bar...Ch. 5 - For the structure in Prob. 5.9, determine the...Ch. 5 - Calculate the reaction at D for the structure...Ch. 5 - Calculate the reaction at D for the structure...Ch. 5 - Determine the tension in each of the three ropes...Ch. 5 - Using only one equilibrium equation, compute the...Ch. 5 - The homogeneous 25-kg bar AB is supported by a...Ch. 5 - The shaft AB is supported by a thrust bearing at A...Ch. 5 - The bar ABCD has a built-in support at A....Ch. 5 - The total weight of the L-shaped beam of constant...Ch. 5 - The bent rod of negligible weight is supported by...Ch. 5 - A 120-lb weight is attached to the cable that is...Ch. 5 - Calculate the force in cable CD and the reaction...Ch. 5 - The 350-lb homogeneous plate has the shape of an...Ch. 5 - The bent rod ABCD is supported by a...Ch. 5 - A hoist is formed by connecting bars BD and BE to...Ch. 5 - The crank arm OD of the winch is connected by a...Ch. 5 - The 80-lb homogeneous plate is supported by a...Ch. 5 - The frame is built into the wall at D and G. The...Ch. 5 - The bent bar of negligible weight is supported by...Ch. 5 - Determine the reactions at ball-and-socket joints...Ch. 5 - The 180-lb homogeneous bar is supported by a...Ch. 5 - The bent rod is supported by a ball-and-socket...Ch. 5 - Find the maximum load P that can be supported by...Ch. 5 - The vertical mast OA, which weighs 1.5 kN, is...Ch. 5 - The homogeneous bar AB weighs 50-lb. End B leans...Ch. 5 - The 500-kg crate is supported by the three cables....Ch. 5 - The uniform bars AB and BC each weigh 4 lb/ft....Ch. 5 - The rigid body of negligible weight is supported...Ch. 5 - The homogeneous 860-kg bar AB is supported by a...Ch. 5 - The triangular plate is supported by three...Ch. 5 - The connections at the ends of bars AB and BC arc...Ch. 5 - The bar AEB is supported by a ball-and-socket...Ch. 5 - The shaft is supported by a thrust bearing at A...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 5. Estimate the friction pressure gradient in a 10.15 cm bore unheated horizontal pipe for the following conditions: Fluid-propylene Pressure 8.175 bar Temperature-7°C Mass flow of liquid-2.42 kg/s. Density of liquid-530 kg/m³ Mass flow of vapour-0.605 kg/s. Density of vapour-1.48 kg/m³arrow_forwardDescribe the following HVAC systems. a) All-air systems b) All-water systems c) Air-water systems Graphically represent each system with a sketch.arrow_forwardTwo large tanks, each holding 100 L of liquid, are interconnected by pipes, with the liquid flowing from tank A into tank B at a rate of 3 L/min and from B into A at a rate of 1 L/min (see Figure Q1). The liquid inside each tank is kept well stirred. A brine solution with a concentration of 0.2 kg/L of salt flows into tank A at a rate of 6 L/min. The diluted solution flows out of the system from tank A at 4 L/min and from tank B at 2 L/min. If, initially, tank A contains pure water and tank B contains 20 kg of salt. A 6 L/min 0.2 kg/L x(t) 100 L 4 L/min x(0) = 0 kg 3 L/min 1 L/min B y(t) 100 L y(0) = 20 kg 2 L/min Figure Q1 - Mixing problem for interconnected tanks Determine the mass of salt in each tank at time t≥ 0: Analytically (hand calculations) Using MATLAB Numerical Functions (ode45) Creating Simulink Model Plot all solutions on the same graph for the first 15 min. The graph must be fully formatted by code.arrow_forward
- ased on the corresponding mass flow rates (and NOT the original volumetric flow rates) determine: a) The mass flow rate of the mixed air (i.e., the combination of the two flows) leaving the chamber in kg/s. b) The temperature of the mixed air leaving the chamber. Please use PyscPro software for solving this question. Notes: For part (a), you will first need to find the density or specific volume for each state (density = 1/specific volume). The units the 'v' and 'a' are intended as subscripts: · kgv = kg_v = kgv = kilogram(s) [vapour] kga = kg_a =kga = kilogram(s) [air]arrow_forwardThe answers to this question s wasn't properly given, I need expert handwritten solutionsarrow_forwardI need expert handwritten solutions to this onlyarrow_forward
- Two large tanks, each holding 100 L of liquid, are interconnected by pipes, with the liquid flowing from tank A into tank B at a rate of 3 L/min and from B into A at a rate of 1 L/min (see Figure Q1). The liquid inside each tank is kept well stirred. A brine solution with a concentration of 0.2 kg/L of salt flows into tank A at a rate of 6 L/min. The diluted solution flows out of the system from tank A at 4 L/min and from tank B at 2 L/min. If, initially, tank A contains pure water and tank B contains 20 kg of salt. A 6 L/min 0.2 kg/L x(t) 100 L 4 L/min x(0) = 0 kg 3 L/min B y(t) 100 L y(0) = 20 kg 2 L/min 1 L/min Figure Q1 - Mixing problem for interconnected tanks Determine the mass of salt in each tank at time t > 0: Analytically (hand calculations)arrow_forwardTwo springs and two masses are attached in a straight vertical line as shown in Figure Q3. The system is set in motion by holding the mass m₂ at its equilibrium position and pushing the mass m₁ downwards of its equilibrium position a distance 2 m and then releasing both masses. if m₁ = m₂ = 1 kg, k₁ = 3 N/m and k₂ = 2 N/m. www.m k₁ = 3 (y₁ = 0). m₁ = 1 k2=2 (y₂ = 0) |m₂ = 1 Y2 y 2 System in static equilibrium (Net change in spring length =32-31) System in motion Figure Q3 - Coupled mass-spring system Determine the equations of motion y₁(t) and y₂(t) for the two masses m₁ and m₂ respectively: Analytically (hand calculations)arrow_forward100 As a spring is heated, its spring constant decreases. Suppose the spring is heated and then cooled so that the spring constant at time t is k(t) = t sin N/m. If the mass-spring system has mass m = 2 kg and a damping constant b = 1 N-sec/m with initial conditions x(0) = 6 m and x'(0) = -5 m/sec and it is subjected to the harmonic external force f(t) = 100 cos 3t N. Find at least the first four nonzero terms in a power series expansion about t = 0, i.e. Maclaurin series expansion, for the displacement: Analytically (hand calculations)arrow_forward
- this is answer to a vibrations question. in the last part it states an assumption of x2, im not sure where this assumption comes from. an answer would be greatly appreciatedarrow_forwardPlease answer with the sketches.arrow_forwardThe beam is made of elastic perfectly plastic material. Determine the shape factor for the cross section of the beam (Figure Q3). [Take σy = 250 MPa, yNA = 110.94 mm, I = 78.08 x 106 mm²] y 25 mm 75 mm I 25 mm 200 mm 25 mm 125 Figure Q3arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Types Of loads - Engineering Mechanics | Abhishek Explained; Author: Prime Course;https://www.youtube.com/watch?v=4JVoL9wb5yM;License: Standard YouTube License, CC-BY