
Concept explainers
Consider the plot of the sinusoidal voltage
- Stretches the sinusoidal curve vertically.
Which statement best describes
b. Increasing the frequency f?
c. Decreasing
d. Decreasing the angular frequency w?
e. Increasing the period?
(a)
Change in sinusoidal voltage graph if peak amplitude is increased.
Answer to Problem 5.1P
Increasing the peak amplitude stretches the sinusoidal curve vertically.
Option (1).
Explanation of Solution
Given information:
Given sinusoidal voltage is
Calculation:
Graph of sinusoidal voltage is
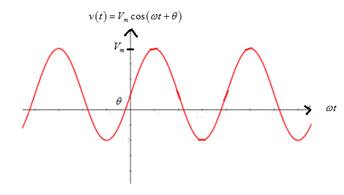
From the graph, it is noted thatif peak amplitude Vm is increased, it stretches the sinusoidal curve vertically.
(b)
Change in sinusoidal voltage graph if frequency is increased.
Answer to Problem 5.1P
Increasing the frequency compresses the sinusoidal curve horizontally.
Option (4).
Explanation of Solution
Given information:
Given sinusoidal voltage is
Calculation:
Graph of sinusoidal voltage is
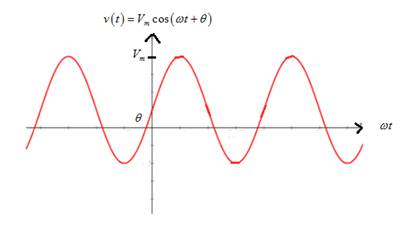
From the graph, it is noted that if the frequency is increased,the time period is reduced so that it compresses the sinusoidal curve horizontally.
(c)
Change in sinusoidal voltage graph if phase angle (theta) is decreased.
Answer to Problem 5.1P
Decreasing the phase angle (theta) translates the sinusoidal curve to the right.
Option (5).
Explanation of Solution
Given information:
Given sinusoidal voltage is
Calculation:
Graph of sinusoidal voltage is
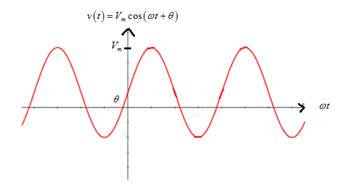
From the graph, it is noted that if the phase angle (theta) is decreased, it translates the sinusoidal curve to the right.
(d)
Change in sinusoidal voltage graph if the angular frequency is decreased.
Answer to Problem 5.1P
Decreasing the angular frequency stretches the sinusoidal voltage graph horizontally.
Option (3).
Explanation of Solution
Given information:
Given sinusoidal voltage is
Calculation:
Graph of sinusoidal voltage is
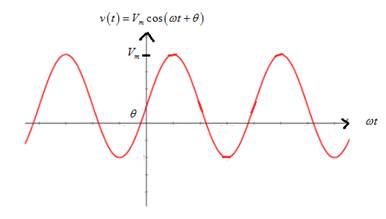
From the graph, it is noted that if the angular frequency is decreased, it increases the time period of the curve,which means it stretches sinusoidal horizontally.
(e)
Change in sinusoidal voltage graph if the time period is increased.
Answer to Problem 5.1P
Increasing the time period stretches the sinusoidal voltage graph horizontally.
Option (3).
Explanation of Solution
Given information:
Given sinusoidal voltage is
Calculation:
Graph of sinusoidal voltage is
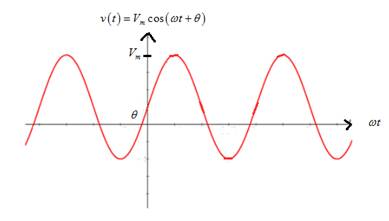
From the graph, it is noted that if time period is increased, it stretches the sinusoidal voltage graph horizontally.
Want to see more full solutions like this?
Chapter 5 Solutions
EBK ELECTRICAL ENGINEERING
Additional Engineering Textbook Solutions
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Computer Science: An Overview (13th Edition) (What's New in Computer Science)
Degarmo's Materials And Processes In Manufacturing
Mechanics of Materials (10th Edition)
Introduction To Programming Using Visual Basic (11th Edition)
Java: An Introduction to Problem Solving and Programming (8th Edition)
- Explain the advantages of three-phase supply for distribution purposes. (b) Assuming the relationship between the line and phase values of currents and voltages, show that the active power input to a three-phase balanced load is √3VI cos φ, where V and I are line quantities. (c) Three similar inductors, each of resistance 10 Ω and inductance 0.019 H, are delta-connected to a three-phase, 400 V, 50 Hz sinusoidal supply. Calcu late: the value of the line current; the power factor and the active power input to the circuit. ANS: 59.5 A, 0.858 lag, 35.5 kWarrow_forwardnot use ai pleasearrow_forwardA three-phase, 400 V, star-connected motor has an output of 50 kW, with an efficiency of 90 per cent and a power factor of 0.85. Calculate the line current. Sketch a phasor diagram showing the voltages and currents. If the motor windings were connected in mesh, what would be the correct voltage of a three phase supply suitable for the motor? ANS: 90.8 A, 240 Varrow_forward
- Don't use ai to answer I will report you answerarrow_forwardShow with the aid of a phasor diagram that for both star- and delta-connected balanced loads, the total active power is given by √3VI cos φ, where V and I are the line values of voltage and current respectively and φ is the angle between phase values of voltage and current. A balanced three-phase load consists of three coils, each of resistance 4 Ω and inductance 0.02 H. Determine the total active power when the coils are (a) star-connected, (b) delta-connected to a 400 V, three phase, 50 Hz supply. ANS:11.56 kW, 34.7 kWarrow_forwardThe load connected to a three-phase supply comprises three similar coils connected in star. The line currents are 25 A and the apparent and active power inputs are 20 kVA and 11 kW respectively. Find the line and phase voltages, reactive power input and the resistance and reactance of each coil. If the coils are now con nected in delta to the same three-phase supply, calculate the line currents and the active power taken. ANS : 462 V, 267 V, 16.7 kvar, 5.87 Ω, 8.92 Ω; 75 A, 33 kWarrow_forward
- A three-phase delta-connected load, each phase of which has an inductive reactance of 40 Ω and a resistance of 25 Ω, is fed from the secondary of a three-phase star-connected transformer which has a phase voltage of 230 V. Draw the circuit diagram of the system and calculate: (a) the current in each phase of the load; (b) the p.d. across each phase of the load; (c) the current in the transformer secondary windings; the total active power taken from the supply and its power factor.arrow_forwardDerive the numerical relationship between the line and phase currents for a balanced three-phase delta connected load. Three coils are connected in delta to a three-phase, three-wire, 400 V, 50 Hz supply and take a line current of 5 A 0.8 power factor lagging. Calculate the resistance and inductance of the coils. If the coils are star-connected to the same supply, calculate the line current and the total power. Calculate the line cur rents if one coil becomes open-circuited when the coils are connected in star. Ans: 110.7 Ω, 0.264 H; 1.67 A, 926 W; 1.445 A, 1.445 A, 0arrow_forwardDerive, for both star- and delta-connected systems, an expression for the total power input for a balanced three-phase load in terms of line voltage, line current and power factor. The star-connected secondary of a transformer supplies a delta-connected motor taking a power of 90 kW at a lagging power factor of 0.9. If the volt age between lines is 600 V, calculate the current in the transformer winding and in the motor winding. Draw circuit and phasor diagrams, properly labelled, showing all voltages and currents in the transformer secondary and the motor. ANS: . 96.2 A, 55.6 Aarrow_forward
- Deduce the relationship between the phase and the line voltages of a three-phase star-connected generator. If the phase voltage of a three-phase star-connected generator is 200 V, what will be the line voltages: (a) when the phases are correctly connected; (b) when the connections to one of the phases are reversed? ans: 346 V; 346 V, 200 V, 200 Varrow_forwardQ2: Given a discrete sequence x(n) = [1,-1,2,4, 1, 3,-1,1] and its spectrum X(k): i. Show that: X(k) =G(k)+WH(k) k=0,1,2,3,4,5,6,7 where G(k) = DFT[g(n)] and H(k) = DFT[h(n)], g(n) and h(n) are even and odd components of x(n) respectively. ii. Compute G(k) and H(k) using the method of computation of DFTS of two real sequences. (15 marks)arrow_forwardQ2: Given a discrete sequence x(n) = [1,-1,2,4, 1, 3,-1,1] and its spectrum X(k): i. Show that: X(k) = G(k)+WH(k) k = 0,1,2,3,4,5,6,7 where G(k) = DFT[g(n)] and H(k) = DFT[h(n)], g(n) and h(n) are even and odd components of x(n) respectively. ii. Compute G(k) and H(k) using the method of computation of DFTS of two real sequences.arrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





