Computer Science: An Overview (12th Edition)
12th Edition
ISBN: 9780133760064
Author: Glenn Brookshear, Dennis Brylow
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5, Problem 40CRP
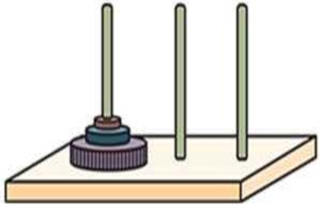
The puzzle called the Towers of Hanoi consists of three pegs, one of which contains several rings stacked in order of descending diameter from bottom to top. The problem is to move the stack of rings to another peg. You are allowed to move only one ring at a time, and at no time is a ring to be placed on top of a smaller one. Observe that if the puzzle involved only one ring, it would be extremely easy. Moreover, when faced with the problem of moving several rings, if you could move all but the largest ring to another peg, the largest ring could then be placed on the third peg, and then the problem would be to move the remaining rings on top of it. Using this observation, develop a recursive
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A hungry mouse wants to eat all four fruits in a maze such as the one below, in as few moves as
possible.. At each turn the mouse can move any number of squares in one of the directions up,
down, left or right, but it is not allowed to enter (or jump over) any walls (i.e., the black squares).
Thus, the mouse moves just like a rook in chess. To eat a fruit, the mouse has to stop at that square.
Assume that the maze has 4 fruits, and the size of b xh squares.
1. Give a suitable representatión of the states in this searching problem.
2. How many possible actions can the mouse perform at each move? (1.e., what is the branching
factor?)
Please answer this only in python
Alice and Bob play a game. At first, there is only one tree with roots. The players take turns,
Alice begins.
At one point, Alice has to pick up any empty underground tree roots (or shrubs) and remove
them. Bob, on the other hand, has to pick out any part of the empty leaves and remove them
from the tree (or trees). (Please note that Bob always takes some depth from the leaves of
the first tree.) It is not allowed to skip the turn. The game ends when the player is unable to
take a chance. Alice's goal is to reduce the number of turns made by both players, while Bob
wants the number to be greater. Considering that they both played very well, how many
turns did they make last.
Input
1
2
12
Output
2
1. The entrance room (or the starting of the maze) is considered as level
1. Now, answer these following questions: (a). Write an algorithm to
figure out how many maximum levels the maze can go up to. (b). Figure
out the complexity of your algorithm.
To create a maze some rooms of a building is connected. Starting room is called Entrance room. From
the entrance room other rooms are there connected from it. However, some rooms of that maze-
building have connected room from it, and some rooms do not have any connected room. Each of the
room can have at most or up to two rooms connected from it. The starting room is the entrance room of
the maze or building. Fore example: It can be any one like the followings:
Exemple -:
Room1
Roono
Room
Entrance
Room Raom
Room2
Room?
Roo
Roomo
Here, maxinum level =7
Example -2;
Entrace
Room D-
Room5
Room 2
Room 4
Maxximum level=3
Chapter 5 Solutions
Computer Science: An Overview (12th Edition)
Ch. 5.1 - Prob. 1QECh. 5.1 - Prob. 2QECh. 5.1 - Prob. 3QECh. 5.1 - Suppose the insertion sort as presented in Figure...Ch. 5.2 - A primitive in one context might turn out to be a...Ch. 5.2 - Prob. 2QECh. 5.2 - The Euclidean algorithm finds the greatest common...Ch. 5.2 - Describe a collection of primitives that are used...Ch. 5.3 - Prob. 2QECh. 5.3 - Prob. 3QE
Ch. 5.3 - Prob. 4QECh. 5.4 - Modify the sequential search function in Figure...Ch. 5.4 - Prob. 2QECh. 5.4 - Some of the popular programming languages today...Ch. 5.4 - Suppose the insertion sort as presented in Figure...Ch. 5.4 - Prob. 5QECh. 5.4 - Prob. 6QECh. 5.4 - Prob. 7QECh. 5.5 - What names are interrogated by the binary search...Ch. 5.5 - Prob. 2QECh. 5.5 - What sequence of numbers would be printed by the...Ch. 5.5 - What is the termination condition in the recursive...Ch. 5.6 - Prob. 1QECh. 5.6 - Give an example of an algorithm in each of the...Ch. 5.6 - List the classes (n2), (log2n), (n), and (n3) in...Ch. 5.6 - Prob. 4QECh. 5.6 - Prob. 5QECh. 5.6 - Prob. 6QECh. 5.6 - Prob. 7QECh. 5.6 - Suppose that both a program and the hardware that...Ch. 5 - Prob. 1CRPCh. 5 - Prob. 2CRPCh. 5 - Prob. 3CRPCh. 5 - Select a subject with which you are familiar and...Ch. 5 - Does the following program represent an algorithm...Ch. 5 - Prob. 6CRPCh. 5 - Prob. 7CRPCh. 5 - Prob. 8CRPCh. 5 - What must be done to translate a posttest loop...Ch. 5 - Design an algorithm that when given an arrangement...Ch. 5 - Prob. 11CRPCh. 5 - Design an algorithm for determining the day of the...Ch. 5 - What is the difference between a formal...Ch. 5 - Prob. 14CRPCh. 5 - Prob. 15CRPCh. 5 - The following is a multiplication problem in...Ch. 5 - Prob. 17CRPCh. 5 - Four prospectors with only one lantern must walk...Ch. 5 - Starting with a large wine glass and a small wine...Ch. 5 - Two bees, named Romeo and Juliet, live in...Ch. 5 - What letters are interrogated by the binary search...Ch. 5 - The following algorithm is designed to print the...Ch. 5 - What sequence of numbers is printed by the...Ch. 5 - Prob. 24CRPCh. 5 - What letters are interrogated by the binary search...Ch. 5 - Prob. 26CRPCh. 5 - Identity the termination condition in each of the...Ch. 5 - Identity the body of the following loop structure...Ch. 5 - Prob. 29CRPCh. 5 - Design a recursive version of the Euclidean...Ch. 5 - Prob. 31CRPCh. 5 - Identify the important constituents of the control...Ch. 5 - Identify the termination condition in the...Ch. 5 - Call the function MysteryPrint (defined below)...Ch. 5 - Prob. 35CRPCh. 5 - Prob. 36CRPCh. 5 - Prob. 37CRPCh. 5 - The factorial of 0 is defined to be 1. The...Ch. 5 - a. Suppose you must sort a list of five names, and...Ch. 5 - The puzzle called the Towers of Hanoi consists of...Ch. 5 - Prob. 41CRPCh. 5 - Develop two algorithms, one based on a loop...Ch. 5 - Design an algorithm to find the square root of a...Ch. 5 - Prob. 44CRPCh. 5 - Prob. 45CRPCh. 5 - Design an algorithm that, given a list of five or...Ch. 5 - Prob. 47CRPCh. 5 - Prob. 48CRPCh. 5 - Prob. 49CRPCh. 5 - Prob. 50CRPCh. 5 - Prob. 51CRPCh. 5 - Does the loop in the following routine terminate?...Ch. 5 - Prob. 53CRPCh. 5 - Prob. 54CRPCh. 5 - The following program segment is designed to find...Ch. 5 - a. Identity the preconditions for the sequential...Ch. 5 - Prob. 57CRPCh. 5 - Prob. 1SICh. 5 - Prob. 2SICh. 5 - Prob. 3SICh. 5 - Prob. 4SICh. 5 - Prob. 5SICh. 5 - Is it ethical to design an algorithm for...Ch. 5 - Prob. 7SICh. 5 - Prob. 8SI
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
Figure 4-3212 shows a class list for Millennium College. Convert this user view to a set of 3NF relations using...
Modern Database Management
The following pseudocode statement calls a function named half, which returns a value that is half that of the ...
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
Will the following statement execute or cause a runtime error? dblResult = CDbl(186,478.39)
Starting Out With Visual Basic (8th Edition)
What type of object should an overloaded operator function return?
Starting Out with C++ from Control Structures to Objects (9th Edition)
Write an SQL statement to display the last name, first name, and email of any owners of cats. Use a subquery. T...
Database Concepts (8th Edition)
In Exercises 55 through 60, find the value of the given function where a and b are numeric variables of type Do...
Introduction To Programming Using Visual Basic (11th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- Note: Answer the question using Java language only. Shaker is the first child who got scholarship into the village. He went to London to study where he finds it very interesting to calculate number of ways of going to point (c, d) from point (a, b) in co-ordinate plane. We can take horizontal and vertical steps only and cannot visit at a point twice. In a step, you can move one unit only. We have to reach to the point (c, d) from the point (a, b) using abs(a-c) + abs(b-d) steps only. Shaker has two sets of points. Set A contains points having X co- ordinate 0 and Y co-ordinates varying from 1 to N (both inclusive). Set B contains points having X co-ordinate K and Y co-ordinates varying from 1 to N (both inclusive). Both sets contain N number of integral points. He wants to calculate the sum of number of ways to going to each point of set B from each point of set A. Input 1 22 Output 8arrow_forwardPython Please. An interesting puzzler for chess buffs is the Knight’s Tour problem, originally proposed by the mathematician Euler. Can the knight piece move around an empty chessboard and touch each of the 64 squares once and only once? We study this intriguing problem in depth here. The knight makes only L-shaped moves (two spaces in one direction and one space in a perpendicular direction). Thus, as shown in the figure below, from a square near the middle of an empty chessboard, the knight (labeled K) can make eight different moves (numbered 0 through 7). A: Draw an eight-by-eight chessboard on a sheet of paper, and attempt a Knight’s Tour by hand. Put a 1 in the starting square, a 2 in the second square, a 3 in the third, and so on. Before starting the tour, estimate how far you think you’ll get, remembering that a full tour consists of 64 moves. How far did you get? Was this close to your estimate? B: Now let’s develop a script that will move the knight around a chessboard…arrow_forwardA tile of a monkey puzzle has four monkey halves that can be labelled as north(N), east (E), south (S), and west (W) half. In addition to the shape of the borderrectangle, these halves determine which edges can be placed next one other. There isalso another way to define how the tiles can be placed: Each tile corner (i.e. compassdirections NE, SE, SW, and NW) has a monkey quarter. If we abstract this quarter, forexample, with a letter, only the tiles with the same letter in their touching corners canbe adjacent. illustrates one valid solution for this quarter monkey puzzle.Are the two monkey puzzle representations equivalent in the sense that if we have apile of ‘half monkey’ tiles H, it is possible to define a pile of ‘quarter monkey’ tilesQ that gives exactly the same set of solutions for the puzzle (and vice versa)?arrow_forward
- When faced with a difficult problem in mathematics, it often helps to draw a picture. If the problem involves a discrete collection of interrelated objects, it is natural to sketch the objects and draw lines between them to indicate the relationships. A graph (composed of dots called vertices connected by lines or curves called edges) is the mathematical version of such a sketch. The edges of a graph may have arrows on them; in this case, the graph is called a directed graph. When we draw a graph, it doesn’t really matter where we put the vertices or whether we draw the edges as curved or straight; rather, what matters is whether or not two given vertices are connected by an edge (or edges). The degree of a vertex is the number of edges incident to it (i.e., the number of times an edge touches it). This is different than the number of edges touching it, because an edge my form a loop; for instance, vertex ? in graph ? (above) has degree 5. In a directed graph, we can speak of the…arrow_forwardThe bean machine is a device for statistical experiments. It consists of an upright board with evenly spaced nails (or pegs) in a triangular form, as shown in Figure 7.13 from our assigned textbook.Balls are dropped from the opening at the top of the board. Every time a ball hits a nail, it has a 50% chance of falling to the left or to the right. The piles of balls are accumulated in the slots at the bottom of the board.Write a program to simulate the bean machine that has 8 slots as shown in the figure. Your program should prompt the user to enter the number of balls to drop. Simulate the falling of each ball by printing its path. For example, the path for the ball in Figure 7.13(b) is LLRRLLR and the path for the ball in Figure 7.13(c) is RLRRLRR. Note that there are 7 levels of nails, so your path should be 7 letters (not 8).Create an array called slots. Each element in slots store the number of balls in a slot. Each ball falls into a slot via a path. The number of “R”s in a path is…arrow_forwardIn computer science and mathematics, the Josephus Problem (or Josephus permutation) is a theoretical problem. Following is the problem statement: There are n people standing in a circle waiting to be executed. The counting out begins at some point (rear) in the circle and proceeds around the circle in a fixed direction. In each step, a certain number (k) of people are skipped and the next person is executed. The elimination proceeds around the circle (which is becoming smaller and smaller as the executed people are removed), until only the last person remains, who is given freedom. Given the total number of persons n and a number k which indicates that k-1 persons are skipped and kth person is killed in circle. The task is to choose the place in the initial circle so that you are the last one remaining and so survive. For example, if n = 5 and k = 2, then the safe position is 3. Firstly, the person at position 2 is killed, then person at position 4 is killed, then person at position 1…arrow_forward
- Write the robot program using the VAL+ for the following automation case. First draw the problem; then handwrite the VAL+ code. The robot picks up FIVE blocks of size 100x100x100 mm that are stacked at a fixed position and place them at the corners and center of a square table of size 500 x 500 mm. Select the original position on the table on your own.arrow_forwardA logical step forward from interactive animated programs is games. The goal of this assignment is to program the classic computer game, Snake. The goal of Snake is to create a snake as long as possible. This is achieved by guiding the snake to an apple on the game board. The snake cannot stop moving, and dies whenever it hits something (excluding apples). Because the snake is growing longer and longer as the game progresses, it gets increasingly difficult to avoid collisions with the snake itself. The player can change the direction of the head of the snake by using the arrow keys. At step in the game, there is always an apple somewhere on the board. If the snake eats an apple, the snake becomes one cell longer. A new apple is placed on a random location, excluding all places covered by the snake. When the snake reaches a side of the game board, it re-emerges at the opposite end. It is probably easiest to understand the game by playing it yourself. You can find a lot of snake…arrow_forwardA chess knight, on one turn, moves either two squares vertically and one horizontally, or two horizontally and one vertically. If we consider a knight starting at the point ⟨x, y⟩ in Z × Z, it has eight possible moves, to ⟨x+1,y+2⟩,⟨x+1,y−2⟩,⟨x−1,y+2⟩,⟨x−1,y−2⟩,⟨x+ 2, y + 1⟩, ⟨x + 2, y − 1⟩, ⟨x − 2, y + 1⟩, or⟨x − 2, y − 1⟩. (a) Prove that given any two points ⟨x, y⟩ and ⟨x′, y′⟩ in Z × Z, there is a sequence of knight moves from the first point to the second. (b) Let a and b be different positive naturals. An (a, b)-knight also has eight possible moves, from ⟨x,y⟩ to ⟨x±a,y±b⟩ or ⟨x±b,y±a⟩. What conditions on a and b allow the (a, b)-knight to go from any point in Z × Z to any other? Prove your answer. (c) If a and b do not meet the conditions of part (b), exactly which points can the (a,b)- knight reach from ⟨x, y⟩arrow_forward
- Can you help me with this code because I am struggling. The Lights Out puzzle consists of an m x n grid of lights, each of which has two states: on and off. The goal of the puzzle is to turn all the lights off, with the caveat that whenever a light is toggled, its neighbors above, below, to the left, and to the right will be toggled as well. If a light along the edge of the board is toggled, then fewer than four other lights will be affected, as the missing neighbors will beignored. In this section, you will investigate the behavior of Lights Out puzzles of various sizes by implementing a LightsOutPuzzle class. Once you have completed the problems in this section, you can test your code in an interactive setting using the provided GUI. See the end of the section for more details. Task: A natural representation for this puzzle is a two-dimensional list of Boolean values, where True corresponds to the on state and False corresponds to the off state. In the LightsOutPuzzle class, write an…arrow_forwardIn programming, we use the mask concept to indicate information that can be shown to the user and information that must be “masked”, that is, hidden. In an implementation of a hangman game, we use a mask to indicate which secret word positions the player has already guessed right (whose the contents must therefore be shown to the player), and which positions must remain hidden. Each time that the player hits a letter of the hidden word, the mask is updated so that it has little dashes in the places of letters that the player has not hit yet and show it, in their proper place, the letters that he already hit it. For example, if the word is "cards", the current mask is: - a - - s and the player guesses the letter "d", the mask should be updated to: - a - ds.Write a function called update_mask that takes as input a string containing the word secret (in the example above, this word would be “cards”), a list whose elements are the characters of the current mask (in the example above…arrow_forwardCan you help me trying to do this code because I am struggling big time with this. question that i need help with: the Eight Puzzle consists of a 3 x 3 board of sliding tiles with a single empty space. For each configuration, the only possible moves are to swap the empty tile with one of its neighboring tiles. The goal state for the puzzle consists of tiles 1-3 in the top row, tiles 4-6 in the middle row, and tiles 7 and 8 in the bottom row, with the empty space in the lower-right corner.you will develop two solvers for a generalized version of the Eight Puzzle, in which the board can have any number of rows and columns. A natural representation for this puzzle is a two-dimensional list of integer values between 0 and r · c -1 (inclusive), where r and c are the number of rows and columns in the board, respectively. In this problem, we will adhere to the convention that the 0-tile represents the empty space.tasks:In the TilePuzzle class, write an initialization method __init__(self,…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education
Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON
Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON
C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON
Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning
Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education
Introduction to Big O Notation and Time Complexity (Data Structures & Algorithms #7); Author: CS Dojo;https://www.youtube.com/watch?v=D6xkbGLQesk;License: Standard YouTube License, CC-BY