Chapter 4.7, Problem 105E

(a)

To determine

To graph $\beta$ as a function of $x$ .

Explanation of Solution

Given information:

A photographer takes a picture of a three foot tall painting hanging in an art gallery. The camera lens is 1 foot below the lower edge of the painting. The angle $\beta$ subtended by the camera lens $x$ feet from the painting is given by

  $\beta =\arctan \frac{3x}{x^2+4},x>0$ .

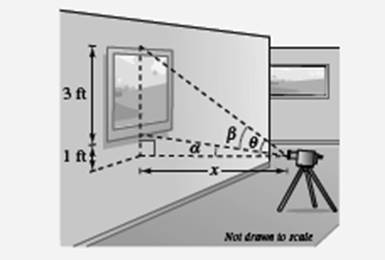
Calculation:

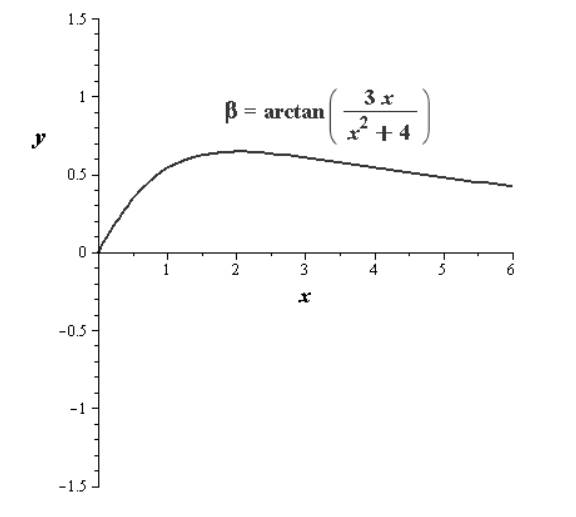
We shall use the graphic utility maple to graph $\beta$ as a function of $x$

The angle $\beta$ subtended by the camera lens $x$ feet from the painting is

  $\beta =\arctan \left(\frac{3x}{x^2+4}\right)$

The graph is as follows

(b)

To determine

To approximate the distance from the picture when $\beta$ is maximum.

Answer to Problem 105E

  $x=2$ feet.

Explanation of Solution

The angle $\beta$ subtended by the camera lens $x$ feet from the painting is

  $\beta =\arctan \left(\frac{3x}{x^2+4}\right)$

The graph is as follows

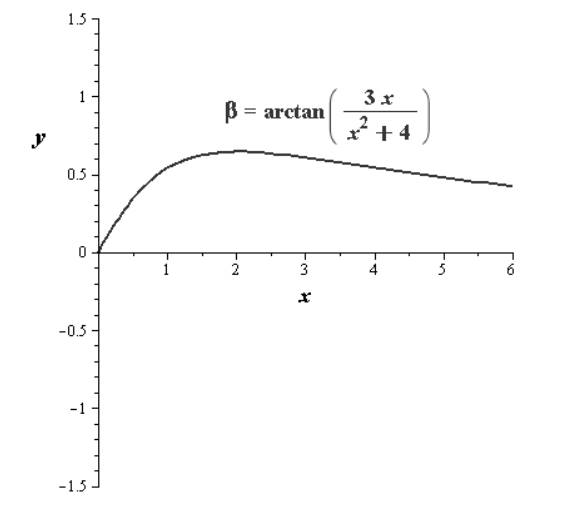
From the graph we can conclude that $\beta$ is maximum when $x=2$ feet.

(c)

To determine

To identify: the asymptote of the graph and interpret its meaning in the context of the problem.

Answer to Problem 105E

The graph has a horizontal asymptote at $\beta =0$ .

Explanation of Solution

The angle $\beta$ subtended by the camera lens $x$ feet from the painting is

  $\beta =\arctan \left(\frac{3x}{x^2+4}\right)$

The graph is as follows

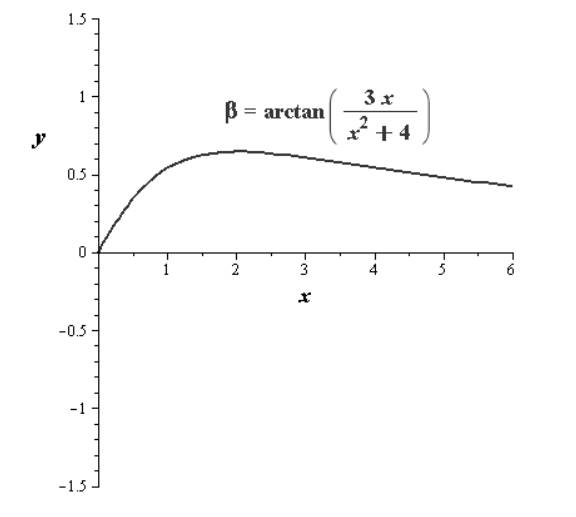
The graph has a horizontal asymptote at $\beta =0$ . Therefore we can conclude that as $x$ increase $\beta$ decreases.