
a.
Find the angle of repose for rock salt.
a.
Answer to Problem 106E
Explanation of Solution
Given information:
Different types of granular substances naturally settle at different angles when stored in cone-shaped piles. This angle
Find the angle of repose for rock salt.
Calculation:
Consider that when rock salt is stored in a cone- shaped pile
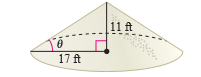
Since the diameter of the base is
Apply the formula of the tangent function in the right-angled triangle containing
Use the TI-83 calculator to evaluate the value of the expression,
Set mode to Radian using keystroke
Use keystrokes
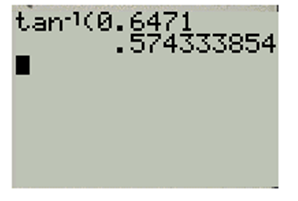
Result which appear is,
Note that the number
Also, note that
Hence angle of repose is
b.
How tall is a pile of rock salt that has a base diameter of
b.
Answer to Problem 106E
Explanation of Solution
Given information:
Different types of granular substances naturally settle at different angles when stored in cone-shaped piles. This angle
How tall is a pile of rock salt that has a base diameter of
Calculation:
Consider that when rock salt is stored in a cone- shaped pile
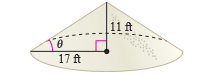
Now the base-diameter of the rock salt is
Let the height of the pile be
Therefore, the angle of repose is a characteristic of granular substance. Hence, angle of repose remains same for this particular type of granular substance that is rock-salt.
Apply the formula of the tangent function in the right-angled triangle containing
Hence, the height of the pile of rock-salt when the diameter of the pile’s base is
Chapter 4 Solutions
EBK PRECALCULUS W/LIMITS
- The graph of f' is below. Use it to determine where the local minima and maxima for f are. If there are multiple answers, separate with commas. 2 f'(x) N -5 -4 3-2-1 -1 -2 -3 -4 12 3 4 5 -x Local minima at x Local maxima at xarrow_forwardThe graph of f' is below. Use it to determine the intervals where f is increasing. -5-4-32 4- 3 2 1 -2 -3 +x 2 3 4 5arrow_forwardThe graph of f' is below. Use it to determine where the inflection points are and the intervals where f is concave up and concave down. If there are multiple inflection points, separate with a comma. 6 5 4 3 2 1 f'(x) +x -6-5-4-3 -2 -1 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6+ Inflection point(s) at x = Concave up: Concave down:arrow_forward
- The graph of f' is below. Use it to determine where the local minima and maxima for f are. If there are multiple answers, separate with commas. f'(x) 4- -5-4-3-8-1 3 2 1 x 1 2 3 4 5 -1 -2 -3 -4 Local minima at a Local maxima at =arrow_forwardThe graph of f' is below. Use it to determine the intervals where f is increasing. f'(xx) 4- -5 -3 -2 3 2 1 1 2 3 4 5 Cit +x 7 2arrow_forwardPlease focus on problem ii.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





