
Concept explainers
a.
Use a variable to indicate the height of the balloon.
a.
Answer to Problem 76E
Explanation of Solution
Given information:
A
Show the known quantities of the triangle and use a variable to indicate the height of the balloon.
Calculation:
The height of the balloon is represented by
b.
Solve an equation for the height of the balloon.
b.
Answer to Problem 76E
Explanation of Solution
Given information:
A
Use a trigonometric function to write and solve an equation for the height of the balloon.
Calculation:
we can see that the length of the hypotenuse of the triangle is
The length of the side opposite to the angle
Now, we know that a trignometric function which involves the two sides, that is the hypotenuse and the opposite side to the angle is the sine function.
Consider a right triangle, with one acute angle
Substituting the values in the above given formula of sin, we have,
Hence, the equation invoolving the unknown quantity
c.
How does this affect the triangle you drew in part (a)?
c.
Answer to Problem 76E
The angle the ballon makes with the ground becomes smaller.
Explanation of Solution
Given information:
A
The breeze becomes stronger and the angle the line makes with the ground decreases. How does this affect the triangle you drew in part (a)?
Calculation:
In order to find the height of the balloon,
Hence,
Now,
Substitute this in equation of
Hence, the height of the ballon is
As the breeza becomes stronger, the hypotenuse of the triangle drwan above tilts more to the ground and hence the angle the ballon makes with the ground becomes smaller. As such the height of the ballon also decreases.
angle
Hence, the angle the ballon makes with the ground becomes smaller.
d.
Complete the table, which shows the heights (in meters) of the balloon for decreasing angle measures
d.
Answer to Problem 76E
Explanation of Solution
Given information:
A
Complete the table, which shows the heights (in meters) of the balloon for decreasing angle measures
Calculation:
We have to find the height of the ballon for decreasing angle measures
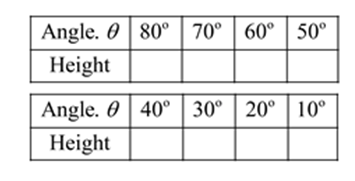
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence,for
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence, for
e.
As
e.
Answer to Problem 76E
The height also approaches zero.
Explanation of Solution
Given information:
A
As
Calculation:
This is because, the height
Hence, we can clearly see that as
Chapter 4 Solutions
EBK PRECALCULUS W/LIMITS
- Find the general solution to the differential equationarrow_forwardcharity savings Budget for May travel food Peter earned $700 during May. The graph shows how the money was used. What fraction was clothes? O Search Submit clothes leisurearrow_forwardExercise 11.3 A slope field is given for the equation y' = 4y+4. (a) Sketch the particular solution that corresponds to y(0) = −2 (b) Find the constant solution (c) For what initial conditions y(0) is the solution increasing? (d) For what initial conditions y(0) is the solution decreasing? (e) Verify these results using only the differential equation y' = 4y+4.arrow_forward
- Aphids are discovered in a pear orchard. The Department of Agriculture has determined that the population of aphids t hours after the orchard has been sprayed is approximated by N(t)=1800−3tln(0.17t)+t where 0<t≤1000. Step 1 of 2: Find N(63). Round to the nearest whole number.arrow_forward3. [-/3 Points] DETAILS MY NOTES SCALCET8 7.4.032. ASK YOUR TEACHER PRACTICE ANOTHER Evaluate the integral. X + 4x + 13 Need Help? Read It SUBMIT ANSWER dxarrow_forwardEvaluate the limit, and show your answer to 4 decimals if necessary. Iz² - y²z lim (x,y,z)>(9,6,4) xyz 1 -arrow_forward
- A graph of the function f is given below: Study the graph of ƒ at the value given below. Select each of the following that applies for the value a = 1 Of is defined at a. If is not defined at x = a. Of is continuous at x = a. If is discontinuous at x = a. Of is smooth at x = a. Of is not smooth at = a. If has a horizontal tangent line at = a. f has a vertical tangent line at x = a. Of has a oblique/slanted tangent line at x = a. If has no tangent line at x = a. f(a + h) - f(a) lim is finite. h→0 h f(a + h) - f(a) lim h->0+ and lim h h->0- f(a + h) - f(a) h are infinite. lim does not exist. h→0 f(a+h) - f(a) h f'(a) is defined. f'(a) is undefined. If is differentiable at x = a. If is not differentiable at x = a.arrow_forwardThe graph below is the function f(z) 4 3 -2 -1 -1 1 2 3 -3 Consider the function f whose graph is given above. (A) Find the following. If a function value is undefined, enter "undefined". If a limit does not exist, enter "DNE". If a limit can be represented by -∞o or ∞o, then do so. lim f(z) +3 lim f(z) 1-1 lim f(z) f(1) = 2 = -4 = undefined lim f(z) 1 2-1 lim f(z): 2-1+ lim f(x) 2+1 -00 = -2 = DNE f(-1) = -2 lim f(z) = -2 1-4 lim f(z) 2-4° 00 f'(0) f'(2) = = (B) List the value(s) of x for which f(x) is discontinuous. Then list the value(s) of x for which f(x) is left- continuous or right-continuous. Enter your answer as a comma-separated list, if needed (eg. -2, 3, 5). If there are none, enter "none". Discontinuous at z = Left-continuous at x = Invalid use of a comma.syntax incomplete. Right-continuous at z = Invalid use of a comma.syntax incomplete. (C) List the value(s) of x for which f(x) is non-differentiable. Enter your answer as a comma-separated list, if needed (eg. -2, 3, 5).…arrow_forwardA graph of the function f is given below: Study the graph of f at the value given below. Select each of the following that applies for the value a = -4. f is defined at = a. f is not defined at 2 = a. If is continuous at x = a. Of is discontinuous at x = a. Of is smooth at x = a. f is not smooth at x = a. If has a horizontal tangent line at x = a. f has a vertical tangent line at x = a. Of has a oblique/slanted tangent line at x = a. Of has no tangent line at x = a. f(a + h) − f(a) h lim is finite. h→0 f(a + h) - f(a) lim is infinite. h→0 h f(a + h) - f(a) lim does not exist. h→0 h f'(a) is defined. f'(a) is undefined. If is differentiable at x = a. If is not differentiable at x = a.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





