
(a)
To Calculate:
The processing fee and write a linear equation to represent the total cost C for t tickets.
(a)
Answer to Problem 45PPS
Processing fee = $15
Linear equation of total cost C for t tickets :
Explanation of Solution
Given Information:
There is a processing fee for each order, and the tickets are $52 each. Jackson ordered 5 tickets and the cost was $275.
Let
C = Total cost per order = $275
t = Number of tickets ordered = 5
b = The processing fee for each order
m = Cost of each ticket = $52
Formula Used:
Equation of slope-intercept form of a line is given by:
Where
Calculation:
First , we form the equation :
Let
C = Total cost per order = $275
t = Number of tickets ordered = 5
b = The processing fee for each order
m = Cost of each ticket = $52
Now, we form the equation :
Cost of 1 ticket = $52
So, cost of t tickets = 52t
The processing fee for each order = b
So, the linear equation ( slope-intercept form) of the total cost C , when t tickets purchased per order:
Now , we find t by substituting the values in (1)
Hence, the processing fee per order = $15.
Substituting the value in equation (1)
The required equation of the total cost C , when t tickets purchased per order:
(b)
To Make :
A table of values for at least three other numbers of tickets.
(b)
Explanation of Solution
Given Information:
From part (a)
Equation of the total cost C , when t tickets purchased per order:
Calculation:
| t | C | (t,C) | |
| 1 | 67 | (1,67) | |
| 2 | 119 | (2,119) | |
| 3 | 174 | (3,174) | |
| 4 | 223 | (4,223) |
(c)
To Graph and Find : The equation
Find cost of 8 tickets.
(c)
Answer to Problem 45PPS
Cost of 8 tickets = $431
Explanation of Solution
Given Information:
From part (a) and (b)
Equation of the total cost C , when t tickets purchased per order:
And points on the line are (1,67) , (2,119)
Graph:
To graph the equation, plot the points (1,67) , (2,119) .
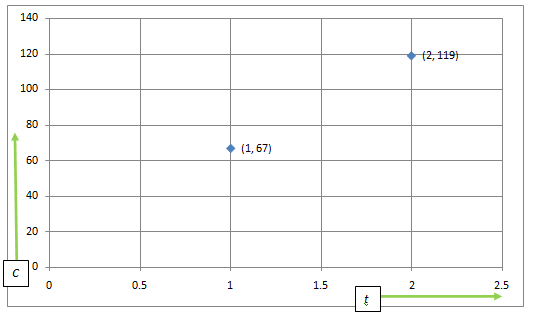
Now , draw a line to connect the points .
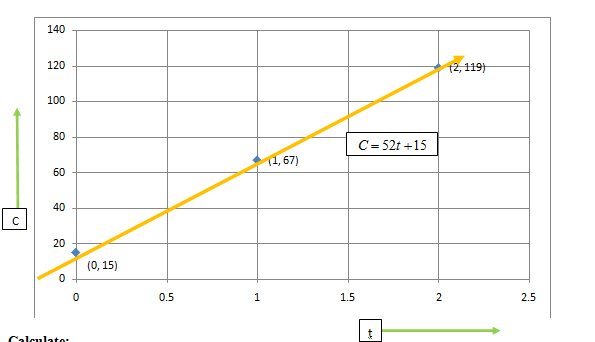
Calculate:
To find cost for 8 tickets:
Hence, cost of 8 tickets is $431
Chapter 4 Solutions
Algebra 1
Additional Math Textbook Solutions
Basic Business Statistics, Student Value Edition
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Thinking Mathematically (6th Edition)
University Calculus: Early Transcendentals (4th Edition)
Introductory Statistics
Pre-Algebra Student Edition
- Solve the following system of equations: 50x+20y=1800 10x+3y=300arrow_forward> > > we are hiring Salesforce Admin Location: Remote Key Responsibilities: Administer Salesforce Sales & Revenue Cloud (CPQ & Billing) Configure workflows, validation rules & dashboards Automate processes using Flows & Process Builder Collaborate with Sales, Finance & Marketing teams Manage user roles & security Apply: Hr@forcecraver.comarrow_forwardAnswer this questionarrow_forward
- 1. vector projection. Assume, ER1001 and you know the following: ||||=4, 7=-0.5.7. For each of the following, explicitly compute the value. འབ (a) (b) (c) (d) answer. Explicitly compute ||y7||. Explain your answer. Explicitly compute the cosine similarity of and y. Explain your Explicitly compute (x, y). Explain your answer. Find the projection of onto y and the projection of onto .arrow_forward2. Answer the following questions using vectors u and v. --0-0-0 = find the the cosine similarity and the angle between u and v. འརྒྱ (a) (b) find the scalar projection of u onto v. (c) find the projection of u onto v. (d) (e) (f) find the scalar projection of onto u. find the projection of u onto u. find the projection of u onto and the projection of onto . (Hint: find the inner product and verify the orthogonality)arrow_forwardPlease type out answerarrow_forward
- The function f(x) = log x is transformed to produce g(x) = log (x) – 3. Identify the type of transformation and describe the change. Please type out answerarrow_forwardEach graph below is the graph of a system of three linear equations in three unknowns of the form Ax = b. Determine whether each system has a solution and, if it does, the number of free variables. A. O free variables ✓ B. no solution C. no solution D. no solution E. 1 free variable F. 1 free variablearrow_forwardSolve the following systems of equations and show all work.y = x2 + 3y = x + 5 Please type out answerarrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





