Introductory Mathematics for Engineering Applications
1st Edition
ISBN: 9781118141809
Author: Nathan Klingbeil
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 4, Problem 26P
A two-link planar robot is shown in Fig. P4.26.
(a) Calculate the position of (lie lip
(b) Determine the magnitude and direction of the position of the robot tip. In other words, write vector
(c) Repeat part (b) using the laws of sines and cosines.
Expert Solution & Answer
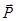
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Write the parametric equations of the line through the point (1,2,3) parallel to the vector a =<2,-1,4>. Also , give the coordinates of another point on this line.
A particle moves linearly from the point (- 2,4) to (10,0) in 4 seconds. Find parametric
equations to describe this motion.
M19
Chapter 4 Solutions
Introductory Mathematics for Engineering Applications
Ch. 4 - Prob. 1PCh. 4 - Prob. 2PCh. 4 - Prob. 3PCh. 4 - Prob. 4PCh. 4 - The tip of a one-link robot is represented as a...Ch. 4 - Repeat problem P4-5 if P=14.42 cm and =123.7.Ch. 4 - Repeat problem P4-5 if P=15 cm and =120.Ch. 4 - Repeat problem P4-5 if P=6 in, and =60.Ch. 4 - The x- and y-components of a vector P shown in...Ch. 4 - The x- and y-components of a vector P shown in...
Ch. 4 - The x- and y-components of a vector P shown in...Ch. 4 - The x- and y-components of a vector P shown in...Ch. 4 - A state trooper investigating an accident pushes a...Ch. 4 - Repeat problem P4-13 if the trooper is applying a...Ch. 4 - In a RL circuit, the voltage across the inductor...Ch. 4 - Repeat problem P4-15 if VR=10 V and VL=15 V.Ch. 4 - In an RC circuit, the voltage across the capacitor...Ch. 4 - Repeat problem P4-17 if VR=10 V and VL=20 V.Ch. 4 - In an electrical circuit, voltage V2 lags voltage...Ch. 4 - In an electrical circuit, voltage V2 leads voltage...Ch. 4 - Prob. 21PCh. 4 - Prob. 22PCh. 4 - Prob. 23PCh. 4 - A ship is crossing a river at a heading of -150...Ch. 4 - Prob. 25PCh. 4 - A two-link planar robot is shown in Fig. P4.26....Ch. 4 - A two-link planar robot is shown in Fig. P4.27....Ch. 4 - A two-link planar robot is shown in Fig. P4.28....Ch. 4 - A two link planar robot is shown in Fig. P4.29....Ch. 4 - Prob. 30PCh. 4 - A weight of 100 kg is suspended from the ceiling...Ch. 4 - Prob. 32PCh. 4 - A vehicle weighing 2000 lb is parked on an...Ch. 4 - A crate of weight W=100 lb sits on a ramp oriented...Ch. 4 - A 500 N television sits on an inclined ramp, shown...Ch. 4 - Prob. 36PCh. 4 - Prob. 37PCh. 4 - A force F=100N is applied to a two-bar truss as...Ch. 4 - Prob. 39PCh. 4 - A waiter extends his arm to hand a plate of food...Ch. 4 - Repeat problem P4-40 if Fm=50 lb, Wa=50 lb, Wp=50...Ch. 4 - Using motion capture, the positions P1 and P2 of...Ch. 4 - Repeat problem P4-42 if P1=1 ft, P2=1.5 ft, 1=45,...
Additional Math Textbook Solutions
Find more solutions based on key concepts
In Problems 18, decide whether or not the method of undetermined coefficients can be applied to find a particul...
Fundamentals of Differential Equations (9th Edition)
In Exercises 51–66, solve the given problems. Refer to Appendix B for units of measurement and their symbols.
...
Basic Technical Mathematics
Evaluate CF(r)dr for given F and C by the method that seems most suitable. Remember that if F is a force, the i...
Advanced Engineering Mathematics
The 16 sequences in the sample space S.
Probability and Statistical Inference (9th Edition)
Testing Hypotheses. In Exercises 13-24, assume that a simple random sample has been selected and test the given...
Elementary Statistics Using The Ti-83/84 Plus Calculator, Books A La Carte Edition (5th Edition)
Solve each problem involving proportions. Price of Gasoline If 6 gallons of premium unleaded gasoline cost $17....
Mathematical Ideas (13th Edition) - Standalone book
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- What are the parametric equations for the line segment from (3,2) to (-10,5)?arrow_forward(3+j5)^4/ (2+j6)^3 answer in polar formarrow_forwardGive the parametric and symmetric equations of the line that passes through the point (4, -3,5) and is perpendicular to both vectors (2, 6, 1) and (1,3,-5).arrow_forward
- Vector A is 6 inches long and is 60° above the +x-axis in the first quadrant. While vector B is 6 inches long and is 60° below the +x-axis (fourth quadrant). Find a) vector sum A + B, b) vector difference B – A.arrow_forwardWhen getting the points from symmetric equation, do we just do x = x0 or we have to divide it by x = x0 / a? Because I did it with x = x0 / a and still got the right answer in other question.arrow_forwarddraw the line which start point (1,1,0) and end point (3,4,0)by using parametric equation.arrow_forward
- Convert the Cartesisan equations x^(2) = 9y and x^(2) - y^(2) =x into polar equations.arrow_forwardfind a vector equation and parametric equations and symmetric equation containing (a,b,c) parallel to di + ejarrow_forwardfind the xy equation of all three sides of triangle ABC with verticies A= (1,5) B= (3, -1) C= (-1, -1)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Vector Addition and Scalar Multiplication, Example 1; Author: patrickJMT;https://www.youtube.com/watch?v=pNMrYACjHXQ;License: Standard YouTube License, CC-BY