
Concept explainers
Summarize the five methods used to prove that the two lines are parallel.
Explanation of Solution
Calculation : s t
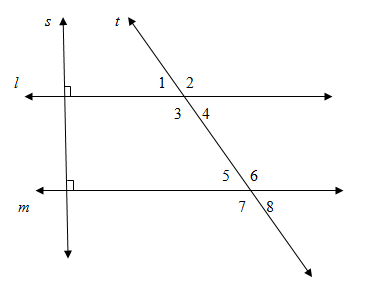
Let l, m be lines , t is transversal such that :
- Alternate Exterior Angle Converse :
If two lines in a plane are cut by a transversal such that a pair of alternate exterior angles is congruent , then the lines are parallel.
t
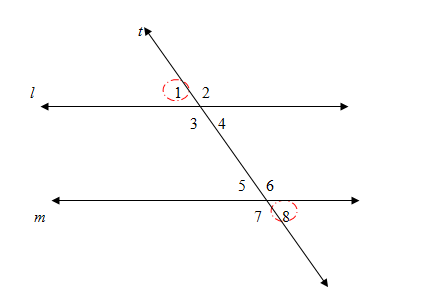
Since ,
- Consecutive Interior Angles Converse :
If two lines in a plane are cut by a transversal such that a pair of consecutive interior angles is supplementary , then the lines are parallel.
t
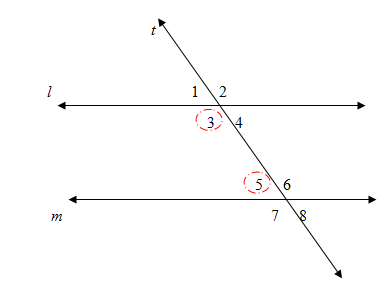
Since ,
- Alternate Interior Angle Converse :
If two lines in a plane are cut by a transversal such that a pair of alternate interior angles is congruent , then the lines are parallel.
t
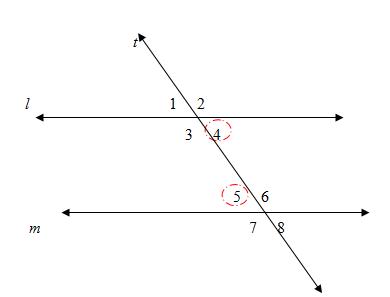
Since ,
- Converse of Corresponding angles Postulate :
If two lines in a plane are cut by a transversal such that corresponding angles are congruent , then they are parallel.
t
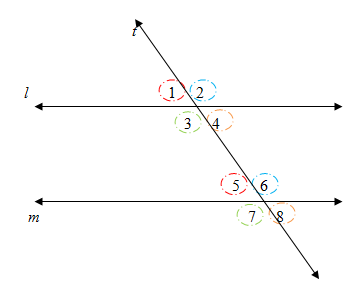
Since ,
- Perpendicular Transversal Converse :
In a plane , if two lines are perpendicular to the same line, then the two lines are parallel.
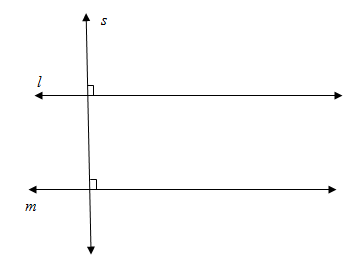
Since ,
Chapter 3 Solutions
Geometry, Student Edition
Additional Math Textbook Solutions
Basic Business Statistics, Student Value Edition
Pre-Algebra Student Edition
University Calculus: Early Transcendentals (4th Edition)
Elementary Statistics (13th Edition)
Calculus: Early Transcendentals (2nd Edition)
A First Course in Probability (10th Edition)
- Can someone help me with this please?arrow_forwardMariela is in her classroom and looking out of a window at a tree, which is 20 feet away. Mariela’s line of sight to the top of the tree creates a 42° angle of elevation, and her line of sight to the base of the tree creates a 31° angle of depression. What is the height of the tree, rounded to the nearest foot? Be sure to show your work to explain how you got your answer.arrow_forward1arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

