Calculus: Graphical, Numerical, Algebraic

3rd Edition

ISBN: 9780133688399

Author: Finney, Ross L.

Publisher: Pearson/Prentice Hall

See similar textbooks

Concept explainers

Limits

When it comes to calculus, limits are considered to be a very important topic of discussion. The main importance of limit lies in expressing the value of a function as it gets closer to a certain value. Also, limits can help you to understand other topic…

Videos

Question

Chapter 3.4, Problem 7E

To determine

To graph: the derivative of the fruit fly population. The graph of the population is reproduced below and what units should be used on the horizontal and vertical axes for the derivative’s graph.

Expert Solution

Answer to Problem 7E

The units for derivative graph are days for horizontal axis (x-axis) and flies per day for the vertical axis (y-axis).

Explanation of Solution

Given information: Populations starting out in closed environments grow slowly at first, when there are relatively few members, then more rapidly as the number of reproducing individual increases and resources are still abundant , then slowly again as the population reaches the carrying capacity of the environment. The graph of the population is reproduced is given below.

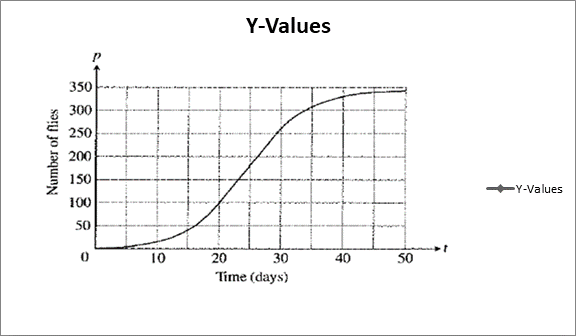
Calculus: Graphical, Numerical, Algebraic, Chapter 3.4, Problem 7E , additional homework tip 1

Calculation:

Estimate the slopes at x =0, 10, and 20,30,40,50 by drawing tangent lines at each value:

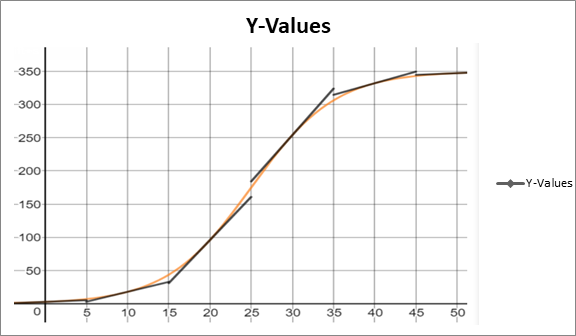
Calculus: Graphical, Numerical, Algebraic, Chapter 3.4, Problem 7E , additional homework tip 2

The estimated slopes of the tangent lines are about 0.5 for t =0, 3 for t =10, 13 for t =20, 14 for t =30, 3.5 for t =40, and 0.5 for t =50. The points on the graph of the derivative are then about (0,0.5),(10,3),(20,13),(30,14),(40,3.5), and (50,0.5). Plot these points and connect them with a smooth curve to make the graph of the derivative :

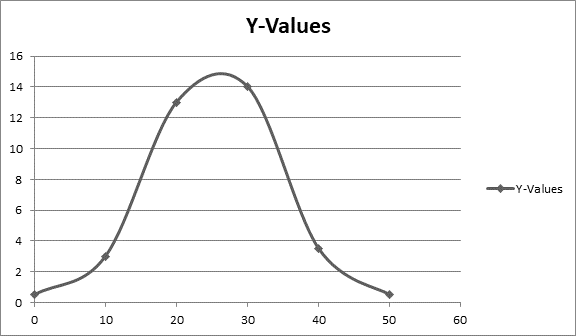
Calculus: Graphical, Numerical, Algebraic, Chapter 3.4, Problem 7E , additional homework tip 3

Since the dependent variable for the original graph was flies and the independent variable was days, the units for derivative graph are days for horizontal axis(x-axis) and flies per day for the vertical axis (y-axis).

To determine

To find: during what days does the population seem to be increasing fastest, slowest.

Expert Solution

Answer to Problem 7E

Fastest: Day 25 and Slowest: Day 0 or Day 50.

Explanation of Solution

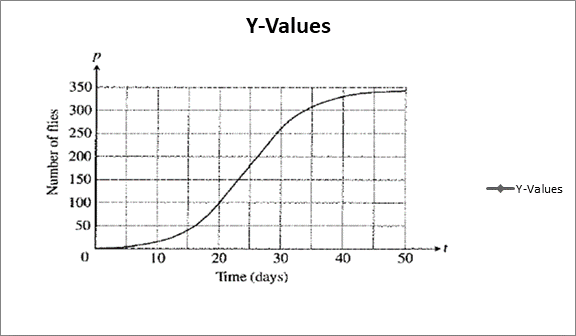
Calculus: Graphical, Numerical, Algebraic, Chapter 3.4, Problem 7E , additional homework tip 4

Calculation:

The derivative graph is shown below.

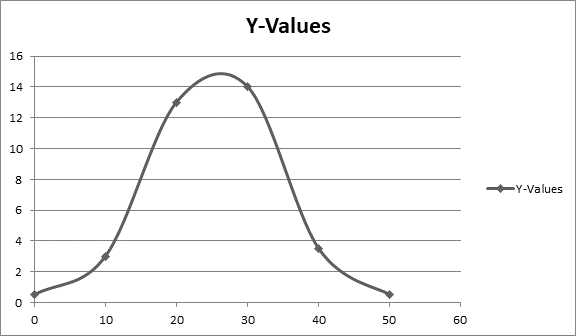
Calculus: Graphical, Numerical, Algebraic, Chapter 3.4, Problem 7E , additional homework tip 5

From the derivative graph, the maximum of the derivative graph was around t =25.

So, Increasing the fastest: Around the 25^t^h day.

From the derivative graph, the minimum of the derivative graph was around t =0 and t =50.

So, increasing the slowest: Day 0 or Day 50.

Chapter 3.4, Problem 6E

Chapter 3.4, Problem 8E

Chapter 3 Solutions

Calculus: Graphical, Numerical, Algebraic

Ch. 3.1 - Prob. 1QR Ch. 3.1 - Prob. 2QR Ch. 3.1 - Prob. 3QR Ch. 3.1 - Prob. 4QR Ch. 3.1 - Prob. 5QR Ch. 3.1 - Prob. 6QR Ch. 3.1 - Prob. 7QR Ch. 3.1 - Prob. 8QR Ch. 3.1 - Prob. 9QR Ch. 3.1 - Prob. 10QR

Ch. 3.1 - Prob. 1E Ch. 3.1 - Prob. 2E Ch. 3.1 - Prob. 3E Ch. 3.1 - Prob. 4E Ch. 3.1 - Prob. 5E Ch. 3.1 - Prob. 6E Ch. 3.1 - Prob. 7E Ch. 3.1 - Prob. 8E Ch. 3.1 - Prob. 9E Ch. 3.1 - Prob. 10E Ch. 3.1 - Prob. 11E Ch. 3.1 - Prob. 12E Ch. 3.1 - Prob. 13E Ch. 3.1 - Prob. 14E Ch. 3.1 - Prob. 15E Ch. 3.1 - Prob. 16E Ch. 3.1 - Prob. 17E Ch. 3.1 - Prob. 18E Ch. 3.1 - Prob. 19E Ch. 3.1 - Prob. 20E Ch. 3.1 - Prob. 21E Ch. 3.1 - Prob. 22E Ch. 3.1 - Prob. 23E Ch. 3.1 - Prob. 24E Ch. 3.1 - Prob. 25E Ch. 3.1 - Prob. 26E Ch. 3.1 - Prob. 27E Ch. 3.1 - Prob. 28E Ch. 3.1 - Prob. 29E Ch. 3.1 - Prob. 30E Ch. 3.1 - Prob. 31E Ch. 3.1 - Prob. 32E Ch. 3.1 - Prob. 33E Ch. 3.1 - Prob. 34E Ch. 3.1 - Prob. 35E Ch. 3.1 - Prob. 36E Ch. 3.1 - Prob. 37E Ch. 3.1 - Prob. 38E Ch. 3.1 - Prob. 39E Ch. 3.1 - Prob. 40E Ch. 3.1 - Prob. 41E Ch. 3.1 - Prob. 42E Ch. 3.1 - Prob. 43E Ch. 3.1 - Prob. 44E Ch. 3.1 - Prob. 45E Ch. 3.2 - Prob. 1QR Ch. 3.2 - Prob. 2QR Ch. 3.2 - Prob. 3QR Ch. 3.2 - Prob. 4QR Ch. 3.2 - Prob. 5QR Ch. 3.2 - Prob. 6QR Ch. 3.2 - Prob. 7QR Ch. 3.2 - Prob. 8QR Ch. 3.2 - Prob. 9QR Ch. 3.2 - Prob. 10QR Ch. 3.2 - Prob. 1E Ch. 3.2 - Prob. 2E Ch. 3.2 - Prob. 3E Ch. 3.2 - Prob. 4E Ch. 3.2 - Prob. 5E Ch. 3.2 - Prob. 6E Ch. 3.2 - Prob. 7E Ch. 3.2 - Prob. 8E Ch. 3.2 - Prob. 9E Ch. 3.2 - Prob. 10E Ch. 3.2 - Prob. 11E Ch. 3.2 - Prob. 12E Ch. 3.2 - Prob. 13E Ch. 3.2 - Prob. 14E Ch. 3.2 - Prob. 15E Ch. 3.2 - Prob. 16E Ch. 3.2 - Prob. 17E Ch. 3.2 - Prob. 18E Ch. 3.2 - Prob. 19E Ch. 3.2 - Prob. 20E Ch. 3.2 - Prob. 21E Ch. 3.2 - Prob. 22E Ch. 3.2 - Prob. 23E Ch. 3.2 - Prob. 24E Ch. 3.2 - Prob. 25E Ch. 3.2 - Prob. 26E Ch. 3.2 - Prob. 27E Ch. 3.2 - Prob. 28E Ch. 3.2 - Prob. 29E Ch. 3.2 - Prob. 30E Ch. 3.2 - Prob. 31E Ch. 3.2 - Prob. 32E Ch. 3.2 - Prob. 33E Ch. 3.2 - Prob. 34E Ch. 3.2 - Prob. 35E Ch. 3.2 - Prob. 36E Ch. 3.2 - Prob. 37E Ch. 3.2 - Prob. 38E Ch. 3.2 - Prob. 39E Ch. 3.2 - Prob. 40E Ch. 3.2 - Prob. 41E Ch. 3.2 - Prob. 42E Ch. 3.2 - Prob. 43E Ch. 3.2 - Prob. 44E Ch. 3.2 - Prob. 45E Ch. 3.2 - Prob. 46E Ch. 3.2 - Prob. 47E Ch. 3.2 - Prob. 48E Ch. 3.3 - Prob. 1QR Ch. 3.3 - Prob. 2QR Ch. 3.3 - Prob. 3QR Ch. 3.3 - Prob. 4QR Ch. 3.3 - Prob. 5QR Ch. 3.3 - Prob. 6QR Ch. 3.3 - Prob. 7QR Ch. 3.3 - Prob. 8QR Ch. 3.3 - Prob. 9QR Ch. 3.3 - Prob. 10QR Ch. 3.3 - Prob. 1E Ch. 3.3 - Prob. 2E Ch. 3.3 - Prob. 3E Ch. 3.3 - Prob. 4E Ch. 3.3 - Prob. 5E Ch. 3.3 - Prob. 6E Ch. 3.3 - Prob. 7E Ch. 3.3 - Prob. 8E Ch. 3.3 - Prob. 9E Ch. 3.3 - Prob. 10E Ch. 3.3 - Prob. 11E Ch. 3.3 - Prob. 12E Ch. 3.3 - Prob. 13E Ch. 3.3 - Prob. 14E Ch. 3.3 - Prob. 15E Ch. 3.3 - Prob. 16E Ch. 3.3 - Prob. 17E Ch. 3.3 - Prob. 18E Ch. 3.3 - Prob. 19E Ch. 3.3 - Prob. 20E Ch. 3.3 - Prob. 21E Ch. 3.3 - Prob. 22E Ch. 3.3 - Prob. 23E Ch. 3.3 - Prob. 24E Ch. 3.3 - Prob. 25E Ch. 3.3 - Prob. 26E Ch. 3.3 - Prob. 27E Ch. 3.3 - Prob. 28E Ch. 3.3 - Prob. 29E Ch. 3.3 - Prob. 30E Ch. 3.3 - Prob. 31E Ch. 3.3 - Prob. 32E Ch. 3.3 - Prob. 33E Ch. 3.3 - Prob. 34E Ch. 3.3 - Prob. 35E Ch. 3.3 - Prob. 36E Ch. 3.3 - Prob. 37E Ch. 3.3 - Prob. 38E Ch. 3.3 - Prob. 39E Ch. 3.3 - Prob. 40E Ch. 3.3 - Prob. 41E Ch. 3.3 - Prob. 42E Ch. 3.3 - Prob. 43E Ch. 3.3 - Prob. 44E Ch. 3.3 - Prob. 45E Ch. 3.3 - Prob. 46E Ch. 3.3 - Prob. 47E Ch. 3.3 - Prob. 48E Ch. 3.3 - Prob. 49E Ch. 3.3 - Prob. 50E Ch. 3.3 - Prob. 51E Ch. 3.3 - Prob. 52E Ch. 3.3 - Prob. 53E Ch. 3.3 - Prob. 54E Ch. 3.3 - Prob. 55E Ch. 3.3 - Prob. 56E Ch. 3.3 - Prob. 57E Ch. 3.3 - Prob. 58E Ch. 3.3 - Prob. 59E Ch. 3.3 - Prob. 1QQ Ch. 3.3 - Prob. 2QQ Ch. 3.3 - Prob. 3QQ Ch. 3.3 - Prob. 4QQ Ch. 3.4 - Prob. 1QR Ch. 3.4 - Prob. 2QR Ch. 3.4 - Prob. 3QR Ch. 3.4 - Prob. 4QR Ch. 3.4 - Prob. 5QR Ch. 3.4 - Prob. 6QR Ch. 3.4 - Prob. 7QR Ch. 3.4 - Prob. 8QR Ch. 3.4 - Prob. 9QR Ch. 3.4 - Prob. 10QR Ch. 3.4 - Prob. 1E Ch. 3.4 - Prob. 2E Ch. 3.4 - Prob. 3E Ch. 3.4 - Prob. 4E Ch. 3.4 - Prob. 5E Ch. 3.4 - Prob. 6E Ch. 3.4 - Prob. 7E Ch. 3.4 - Prob. 8E Ch. 3.4 - Prob. 9E Ch. 3.4 - Prob. 10E Ch. 3.4 - Prob. 11E Ch. 3.4 - Prob. 12E Ch. 3.4 - Prob. 13E Ch. 3.4 - Prob. 14E Ch. 3.4 - Prob. 15E Ch. 3.4 - Prob. 16E Ch. 3.4 - Prob. 17E Ch. 3.4 - Prob. 18E Ch. 3.4 - Prob. 19E Ch. 3.4 - Prob. 20E Ch. 3.4 - Prob. 21E Ch. 3.4 - Prob. 22E Ch. 3.4 - Prob. 23E Ch. 3.4 - Prob. 24E Ch. 3.4 - Prob. 25E Ch. 3.4 - Prob. 26E Ch. 3.4 - Prob. 27E Ch. 3.4 - Prob. 28E Ch. 3.4 - Prob. 29E Ch. 3.4 - Prob. 30E Ch. 3.4 - Prob. 31E Ch. 3.4 - Prob. 32E Ch. 3.4 - Prob. 33E Ch. 3.4 - Prob. 34E Ch. 3.4 - Prob. 35E Ch. 3.4 - Prob. 36E Ch. 3.4 - Prob. 37E Ch. 3.4 - Prob. 38E Ch. 3.4 - Prob. 39E Ch. 3.4 - Prob. 40E Ch. 3.4 - Prob. 41E Ch. 3.4 - Prob. 42E Ch. 3.4 - Prob. 43E Ch. 3.4 - Prob. 44E Ch. 3.4 - Prob. 45E Ch. 3.4 - Prob. 46E Ch. 3.4 - Prob. 47E Ch. 3.4 - Prob. 48E Ch. 3.4 - Prob. 49E Ch. 3.4 - Prob. 50E Ch. 3.5 - Prob. 1QR Ch. 3.5 - Prob. 2QR Ch. 3.5 - Prob. 3QR Ch. 3.5 - Prob. 4QR Ch. 3.5 - Prob. 5QR Ch. 3.5 - Prob. 6QR Ch. 3.5 - Prob. 7QR Ch. 3.5 - Prob. 8QR Ch. 3.5 - Prob. 9QR Ch. 3.5 - Prob. 10QR Ch. 3.5 - Prob. 1E Ch. 3.5 - Prob. 2E Ch. 3.5 - Prob. 3E Ch. 3.5 - Prob. 4E Ch. 3.5 - Prob. 5E Ch. 3.5 - Prob. 6E Ch. 3.5 - Prob. 7E Ch. 3.5 - Prob. 8E Ch. 3.5 - Prob. 9E Ch. 3.5 - Prob. 10E Ch. 3.5 - Prob. 11E Ch. 3.5 - Prob. 12E Ch. 3.5 - Prob. 13E Ch. 3.5 - Prob. 14E Ch. 3.5 - Prob. 15E Ch. 3.5 - Prob. 16E Ch. 3.5 - Prob. 17E Ch. 3.5 - Prob. 18E Ch. 3.5 - Prob. 19E Ch. 3.5 - Prob. 20E Ch. 3.5 - Prob. 21E Ch. 3.5 - Prob. 22E Ch. 3.5 - Prob. 23E Ch. 3.5 - Prob. 24E Ch. 3.5 - Prob. 25E Ch. 3.5 - Prob. 26E Ch. 3.5 - Prob. 27E Ch. 3.5 - Prob. 28E Ch. 3.5 - Prob. 29E Ch. 3.5 - Prob. 30E Ch. 3.5 - Prob. 31E Ch. 3.5 - Prob. 32E Ch. 3.5 - Prob. 33E Ch. 3.5 - Prob. 34E Ch. 3.5 - Prob. 35E Ch. 3.5 - Prob. 36E Ch. 3.5 - Prob. 37E Ch. 3.5 - Prob. 38E Ch. 3.5 - Prob. 39E Ch. 3.5 - Prob. 40E Ch. 3.5 - Prob. 41E Ch. 3.5 - Prob. 42E Ch. 3.5 - Prob. 43E Ch. 3.5 - Prob. 44E Ch. 3.5 - Prob. 45E Ch. 3.5 - Prob. 46E Ch. 3.5 - Prob. 47E Ch. 3.5 - Prob. 48E Ch. 3.5 - Prob. 49E Ch. 3.5 - Prob. 50E Ch. 3.5 - Prob. 51E Ch. 3.5 - Prob. 52E Ch. 3.5 - Prob. 1QQ Ch. 3.5 - Prob. 2QQ Ch. 3.5 - Prob. 3QQ Ch. 3.5 - Prob. 4QQ Ch. 3 - Prob. 1RE Ch. 3 - Prob. 2RE Ch. 3 - Prob. 3RE Ch. 3 - Prob. 4RE Ch. 3 - Prob. 5RE Ch. 3 - Prob. 6RE Ch. 3 - Prob. 7RE Ch. 3 - Prob. 8RE Ch. 3 - Prob. 9RE Ch. 3 - Prob. 10RE Ch. 3 - Prob. 11RE Ch. 3 - Prob. 12RE Ch. 3 - Prob. 13RE Ch. 3 - Prob. 14RE Ch. 3 - Prob. 15RE Ch. 3 - Prob. 16RE Ch. 3 - Prob. 17RE Ch. 3 - Prob. 18RE Ch. 3 - Prob. 19RE Ch. 3 - Prob. 20RE Ch. 3 - Prob. 21RE Ch. 3 - Prob. 22RE Ch. 3 - Prob. 23RE Ch. 3 - Prob. 24RE Ch. 3 - Prob. 25RE Ch. 3 - Prob. 26RE Ch. 3 - Prob. 27RE Ch. 3 - Prob. 28RE Ch. 3 - Prob. 29RE Ch. 3 - Prob. 30RE Ch. 3 - Prob. 31RE Ch. 3 - Prob. 32RE Ch. 3 - Prob. 33RE Ch. 3 - Prob. 34RE Ch. 3 - Prob. 35RE Ch. 3 - Prob. 36RE Ch. 3 - Prob. 37RE Ch. 3 - Prob. 38RE Ch. 3 - Prob. 39RE Ch. 3 - Prob. 40RE Ch. 3 - Prob. 41RE Ch. 3 - Prob. 42RE Ch. 3 - Prob. 43RE Ch. 3 - Prob. 44RE Ch. 3 - Prob. 45RE Ch. 3 - Prob. 46RE Ch. 3 - Prob. 47RE Ch. 3 - Prob. 48RE Ch. 3 - Prob. 49RE Ch. 3 - Prob. 50RE Ch. 3 - Prob. 51RE Ch. 3 - Prob. 52RE Ch. 3 - Prob. 53RE Ch. 3 - Prob. 54RE Ch. 3 - Prob. 55RE Ch. 3 - Prob. 56RE Ch. 3 - Prob. 57RE Ch. 3 - Prob. 58RE Ch. 3 - Prob. 59RE Ch. 3 - Prob. 60RE Ch. 3 - Prob. 61RE Ch. 3 - Prob. 62RE Ch. 3 - Prob. 63RE Ch. 3 - Prob. 64RE Ch. 3 - Prob. 65RE Ch. 3 - Prob. 66RE Ch. 3 - Prob. 67RE Ch. 3 - Prob. 68RE Ch. 3 - Prob. 69RE Ch. 3 - Prob. 70RE Ch. 3 - Prob. 71RE Ch. 3 - Prob. 72RE Ch. 3 - Prob. 73RE Ch. 3 - Prob. 74RE Ch. 3 - Prob. 75RE Ch. 3 - Prob. 76RE Ch. 3 - Prob. 77RE Ch. 3 - Prob. 78RE Ch. 3 - Prob. 79RE Ch. 3 - Prob. 80RE Ch. 3 - Prob. 81RE Ch. 3 - Prob. 82RE Ch. 3 - Prob. 83RE

Additional Math Textbook Solutions

Find more solutions based on key concepts

Derivatives of bx Find the derivatives of the following functions. 23. y = 8x

Calculus: Early Transcendentals (2nd Edition)

Confidence Intervals. In Exercises 9–24, construct the confidence interval estimate of the mean. 12. Atkins Wei...

Elementary Statistics (13th Edition)

Identifying Type I and Type II Errors In Exercises 31–36, describe type I and type II errors for a hypothesis t...

Elementary Statistics: Picturing the World (7th Edition)

Fill in each blank so that the resulting statement is true. The quadratic function f(x)=a(xh)2+k,a0, is in ____...

Algebra and Trigonometry (6th Edition)

The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...

Basic Business Statistics, Student Value Edition

A box contains 3 marbles: 1 red, 1 green, and 1 blue. Consider an experiment that consists of taking 1 marble f...

A First Course in Probability (10th Edition)

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.