
Concept explainers
a.
To graph: the truck’s velocity v=ds/dt for
a.
Answer to Problem 26E
Explanation of Solution
Given information: The graph shows the position s of truck traveling on a highway. The Truck starts at t =0 and return 15 hours later at t =15.
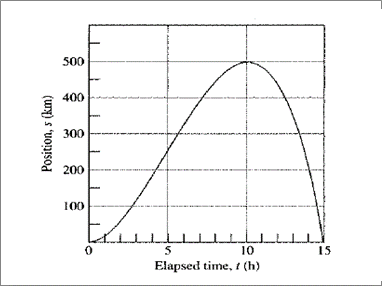
Calculation:
The velocity function v (in dark blue) is the derivative of the position function is s. The derivative at point t gives the slope of the tangent line to the original function at point t.
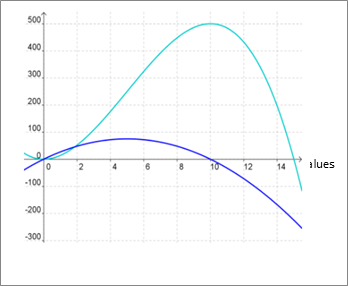
Starting at t = 0. The tangent to s is horizontal so v=0. Following along the curve of s up to about t = 5, the slope of the tangent lines are increasing, so v increases in the same interval.
After t =5, the slope of the tangent lines starts to decrease until it gets horizontal again at t =10. So from t =5 to t = 10, v decreases and goes back to 0.
After t = 10, the slope of the tangent lines becomes increasingly negative all the way through t = 15. So after t = 10, v is increasingly negative.

Acceleration a (in red) is the derivative of velocity because the derivative is just the slope of the tangent lines. Before t = 5, the slope of the tangent to v are positive but decreasing to 0. So a is positive and decreasing to 0 at t = 5.
After t = 5. The slope of the tangent to v is negative and continues to decrease at the same rate.
So a is negative and continues in the same direction.
b.
To graph: ds/dt and
b.
Answer to Problem 26E
Explanation of Solution
Given information: The graph shows the position s of truck traveling on a highway. The Truck starts at t =0 and return 15 hours later at t =15.
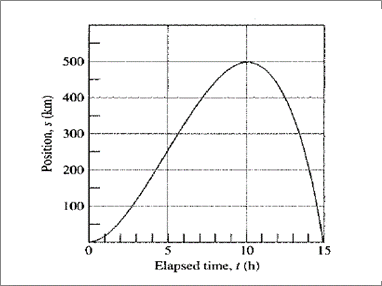
Calculation:
Given s, so find the first and second derivative using power rule.
The graph of s, v=ds/dt and
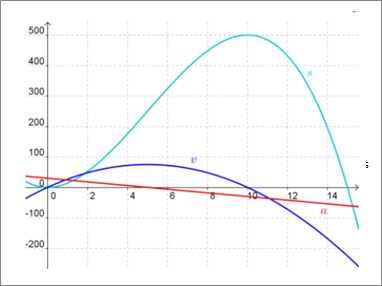
For all of them the horizontal axis is t in hours, but for v the vertical axis is km per hours and for a if is km/
Chapter 3 Solutions
Calculus: Graphical, Numerical, Algebraic
Additional Math Textbook Solutions
Thinking Mathematically (6th Edition)
University Calculus: Early Transcendentals (4th Edition)
Elementary Statistics
College Algebra (7th Edition)
Pre-Algebra Student Edition
Elementary Statistics: Picturing the World (7th Edition)
- Prove 11.1.2arrow_forward39. (a) Show that Σeak converges for each α > 0. (b) Show that keak converges for each a > 0. k=0 (c) Show that, more generally, Σk"eak converges for each k=0 nonnegative integer n and each a > 0.arrow_forward#3 Find the derivative y' = of the following functions, using the derivative rules: dx a) y-Cos 6x b) y=x-Sin4x c) y=x-Cos3x d) y=x-R CD-X:-:TCH :D:D:D - Sin f) Sin(x²) (9) Tan (x³)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





